Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T11:13:33.373Z Has data issue: false hasContentIssue false
  • English
  • Français

Application of Game Theory to Some Problems in Automobile Insurance*)

Published online by Cambridge University Press:  29 August 2014

Karl Borch
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall study the problem of determining “correct” premium rates for sub-groups of an insurance collective. This problem obviously occurs in all branches of insurance. However, it seems at present to be a really burning issue in automobile insurance. We shall show that the problem can be formulated as a conflict between groups which can gain by co-operating, although their interests are opposed. When formulated in this way, the problem evidently can be analysed and solved by the help ot the “Game Theory” of Von Neumann and Morgenstern (5).

We shall first illustrate the problem by a simple example. We consider a group of n1 = 100 persons, each of whom may suffer a loss of 1, with probability p1 = 0.1. We assume that these persons consider forming an insurance company to cover themselves against this risk. We further assume that for some reason, government regulations or prejudices of managers, an insurance company must be organized so that the probability of ruin is less than 0.001

If such a company is formed, expected claim payment will be

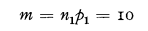
and the standard deviation of the claim payments will be

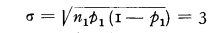
If the government inspection (or the company's actuary) agrees that the ruin probability can be calculated with sufficient approximation by assuming that the claim payments have a normal distribution, the company must have funds amounting to

Type
Papers
Information
ASTIN Bulletin: The Journal of the IAA , Volume 2 , Issue 2 , September 1962 , pp. 208 - 221
Copyright
Copyright © International Actuarial Association 1962

Footnotes

*)

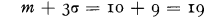
Paper presented to the Juan-les-Pins Colloquium 1962.

References

(1)Borch, Karl, “The Utility Concept applied to the Theory of Insurance”, The ASTIN Bulletin Vol. I (1961), pp. 245–255.CrossRefGoogle Scholar
(2)Harsanyi, John C., “A bargaining model for the cooperative n-person game”, Annals of Mathematical Studies, No. 40, pp. 325–355, Princeton 1959Google Scholar
(3)Luce, R. Duncan and Raiffa, Howard, “Games and Decisions”, John Wiley & Sons 1957.Google Scholar
(4)Nash, John F., “The bargaining problem”, Econometrica 1950, pp.155–162.Google Scholar
(5)Neumann, John von and Morgenstern, Oskar, “Theory of Games and Economic Behavior”, Princeton 1944.Google Scholar
(6)Shapley, Lloyds S., “A value for n-person games”, Annals of Mathematical Studies, No. 28, pp. 307–317, Princeton 1953.Google Scholar
(7)Thepaut, A., “Quelques réflexions sur la réforme du tarif français d'assurance automobile”, The ASTIN Bulletin, Vol. II (1962) pp. 109–119.CrossRefGoogle Scholar