Dans plusieurs études [1] Ammeter a démontré que la distribution binomiale négative généralisée peut être interprétée de différentes manières, à savoir comme
a. une contagion des probabilités (Pólya-Eggenberger);
b. une distribution de Poisson basée sur des probabilités fondamentales variables;
c. une distribution de Poisson où la probabilité fondamentale de sinistres n'est pas suffisamment connue;
d. une distribution de Poisson par rapport aux événements, où un seul événement peut comporter plusieurs prétentions de sinistres;
e. une distribution de Poisson basée sur une modification de la répartition des montants de sinistres.
On a, en effet, les relations suivantes:
a. la contagion des probabilités
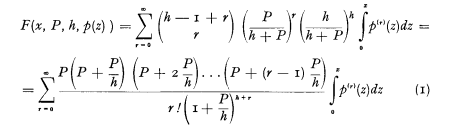
où F(x, P, h, p(z)) représente la probabilité que le sinistre est au plus égal à x dans un intervalle de temps où le sinistre probable est P. x et P y sont exprimés en le sinistre moyen par événement. p(z)dz est la fonction de fréquence du sinistre par événement.
Nous posons 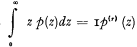 est la convolution de p(z) avec p(z), faite r fois, tandis que h est la notation du paramètre qui figure dans la distribution binomiale négative. Si h est égal à ∞ nous obtenons comme fonction de répartition pour le nombre d'événements survenus la distribution de Poisson.
est la convolution de p(z) avec p(z), faite r fois, tandis que h est la notation du paramètre qui figure dans la distribution binomiale négative. Si h est égal à ∞ nous obtenons comme fonction de répartition pour le nombre d'événements survenus la distribution de Poisson.