Contribution a l'etude du comportement optimum de la cédante et du réassureur dans le cadre de la théorie collective du risque

Extract

a) On peut caractériser la situation du portefeuille d'une société d'assurance par:

le montant de ses réserves libres: Z

le coefficient de sécurité attaché aux primes pures P encaissées: λ

la fonction de fréquence des montants de sinistre: ν(x)

le bénéfice ou gain moyen par prime pure unitaire: δλ

Aux trois premiers élements correspond une probabilité de ruine ε; nous définissons cette dernière comme la probabilité d'extinction d'un fonds de valeur initiale Z, alimenté par des primes (I + λ) P et débité des montants de sinistre x liquidés ou mis en réserve, soit pendant une période infinie ou finie (processus de ruine continu), soit à des époques fixées d'avance, (processus de ruine discontinu).

Cette probabilité de ruine peut, dans des hypothèses assez générates, s'exprimer par:

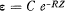
où C est une fonction, dont la valeur est inférieure à l'unité, de λ et éventuellement de Z et de la longueur μ de la période considérée.