Commentaires sur les constatations expérimentales d'une Compagnie Française en matière d'Assurance Responsabilité Civile Automobile pour la période de 1949 à 1959 et méthode préconisée pour la détermination du prix de revient moyen d'une catégorie de risques bien définie.

De nombreux travaux actuariels ou statistiques ont été effectués dans tous les pays pour rechercher les lois pouvant régir les primes d'assurance Automobile en fonction de certaines variables.

Il ne semble pas toutefois que ces travaux théoriques soient facilement exploitables dans la pratique, étant donné les difficultés de saisir d'une manière suffisamment approchée les valeurs réelles des variables.

Notamment, en matière d'assurance Responsabilité Civile Automobile, l'expérience française montre que dans les éléments pouvant servir au calcul des primes, seul parait suffisamment connu à ce jour, le nombre des véhicules exposés au risque.

Dans une Conférence faite à l'Institut des Actuaires Français M. Constant a exposé ses recherches d'une loi de distribution permettant de déterminer les variations du coût moyen des sinistres en fonction des variations d'indices économiques, mais il ne semble pas qu'une utilisation pratique de cette théorie ait pu être obtenue dans le cadre des Entreprises d'Assurances Françaises.

C'est pourquoi il m'a paru bon d'exposer ci-après les résultats d'une méthode expérimentale utilisée dans une importante Compagnie d'Assurance Française pour apprécier si des corrélations peuvent apparaître entre la variation du coût moyen des sinistres et la variation du ou de plusieurs indices économiques. Cette méthode par ailleurs, donne également un moyen pour déterminer un nombre théorique de sinistres qui soit à l'abri des modifications importantes que les déclarations de sinistres — seul élément connu dans les Compagnies — peuvent subir selon certaines conjonctures.

In his comprehensive paper entitled “A General Survey of Problems Involved in Motor Insurance”, Dr. Carl Philipson includes remarks with respect to mathematical reserves. The purpose of this paper is to discuss a method of statistical estimation of Third Party Motor Insurance claim reserves. These methods can also be used for Car Damage Insurance, since reserve determination for these rapid settlement property coverages is simpler than for Third Party lines.

Dr. Philipson mentions the two main purposes of claim reservesbalance sheet loss reserves which shall be estimated on the safe side for financial reasons, and those reserves needed for risk statistics. In this paper I shall confine my subject to aggregate loss reserves for financial statements and internal management operating reports.

In this paper, it will be convenient to refer to both European and U.S. terminology for Motor Car and Automobile Insurance.

The comparable terms are:

The accident year is the important fiscal period underlying not only the statistical estimation methods discussed in this paper but it is also the basic grouping of accidents in the official reserve tests required in the Annual Statements of U.S. companies for casualty and property lines. An accident year embraces the entire population of claims incurred with accident dates in a particular calendar year, whether reported to the company in that year or subsequently (i.e., incurred /not reported).

La question posée au colloque constitue un cas particulier du problème de la chance et de la malchance. Il appartient à une catégorie plus large de problèmes qui touche aussi bien à la statistique qu'à la recherche opérationnelle.

Pour une catégorie de risque déterminée, il faut définir deux éléments essentiels.

a) pour une période de temps de référence conventionnelle — la semaine par exemple, il faut disposer de la loi de survenance des sinistres c'est-à-dire que pour la période de temps considérée, il faut disposer de la loi qui constate qu'il se présente

la fonction génératrice de cette loi de survenance, toujours définie pour o ≤ s ≤ 1.

b) pour la catégorie de risques, nous considérons d'autre part la fonction de distribution des sinistres survenus.

S désignant la variable aléatoire du montant du sinistre, m la somme payée.

Ces deux éléments essentiels peuvent être donnés soit sur leur forme mathématique (fonctions spécifiées) sont sur leur forme expérimentale (image statistique d'un échantillon).

The Ministry of Social Affairs, which acts i.a. as the supervising office in Finland, has given instructions regarding the normal reserves of insurance companies. A summary of these and some comments are given here as far as they concern motor-vehicle insurance. The instructions as far as they concern the subject referred to in the following in the items 2-6, 9 and 10, were compiled by a committee, presided over by Mr. I. Ketola, M. Sc, which availed itself of the experience of several Finnish insurance companies.

In order to give a review of the system as a whole many items, which are mathematically trivial and well-known, are briefly explained.

The conventional principle of “pro rata parte temporis” is followed, which leads to the well-known reserve

where P is the premium income of the company. This provides that the days when the premiums fall due are approximately equally distributed over the year (which can be checked from the premium sums of the different months in the book-keeping) or at least have no cluster points in the second half of the year and that the cost of the collecting of premiums is not less than 0.2 P. A more accurate calculation takes into account i.a. temporary short term policies etc.

In casu-reserve. All unpaid claims (except those mentioned later) due to accidents which occured before the end of the account year, are listed and rated one by one. Doubtful cases, e.g. where the cause of the accident is still under litigation, are calculated in accordance with the “worst” alternative.

a) On peut caractériser la situation du portefeuille d'une société d'assurance par:

le montant de ses réserves libres: Z

le coefficient de sécurité attaché aux primes pures P encaissées: λ

la fonction de fréquence des montants de sinistre: ν(x)

le bénéfice ou gain moyen par prime pure unitaire: δλ

Aux trois premiers élements correspond une probabilité de ruine ε; nous définissons cette dernière comme la probabilité d'extinction d'un fonds de valeur initiale Z, alimenté par des primes (I + λ) P et débité des montants de sinistre x liquidés ou mis en réserve, soit pendant une période infinie ou finie (processus de ruine continu), soit à des époques fixées d'avance, (processus de ruine discontinu).

Cette probabilité de ruine peut, dans des hypothèses assez générates, s'exprimer par:

où C est une fonction, dont la valeur est inférieure à l'unité, de λ et éventuellement de Z et de la longueur μ de la période considérée.

In the discussion in the ASTIN Colloquium 1962, which followed my lecture on the numerical evaluation of the distribution functions defining some compound Poisson processes, a remark was made, which drew my attention to the paper quoted here below under reference number (1), On composed Poisson distributions I.

As I have the impression that this remark may induce some confusion of the terms “compound” and “composed”, the more as the same French word (composé) is used for the two terms, a comparison between the two kinds of processes shall be made.

1. The most general propositions of (1) are a theorem which concerns a general homogeneous Markoff process (1.c. § 2) and a theorem for the family {P(k,p)} of distribution functions of positive integervalued variables with mean p, where p runs over all non-negative numbers, and where the convolution of P(k,p1) and P(k,p2) is equal to P(k,p1 + p2) (l.c. § 3). By these propositions the characteristic functions corresponding in the 1st case to the distribution functions defining the homogeneous Markoff process, and in the 2nd case to the distribution functions belonging to the family {P(k,p)} can all be written in the same form, namely

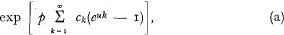
where u is an entirely imaginary variable, p is the parameter of the process, respectively of P(k,p) and c1, c2 … non-negative constants such that 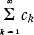converges. If, in the 1st case, 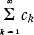converges, and as, in the 2nd case, this series converges, the distributions defined by these characteristic functions are called composed Poisson distributions, which define homogeneous composed Poisson processes.

The need and extent of reinsurance of third party motor insurance depends fundamentally on the risk limits prescribed in the legislation of the country in question (and on the other hand the legal limits of the compulsory insurance may have been fixed with regard to the reasonable possibilities of the insurers getting reinsurance). There are two kinds of risk limits which are applied in different countries: total limits and individual limits. The former defines the maximum joint indemnity for an accident, paid to all claiments together, and the latter defines the maximum indemnity paid to each claiment separately. From the social point of view limits of this sort are not expedient, especially in regard to physical injuries. Owing to this total limit the indemnity for a single claiment can depend on the number of other claiments, which is quite inadequate from the point of view of the actual need to get insurance cover for injuries. The individual lump sum limit allows full compensation for slight injuries but can cut down the compensation for serious ones, which is an irrational method of settling an indemnity system. Owing to these risk limits motor car drivers may also be held responsible for the extra claims personally on the basis of civil (or criminal) law, which compels them to take an extra third party liability insurance (which often also has risk limits).