Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cárdenas, M.
Lasheras, F. F.
Quintero, A.
and
Roy, R.
2016.
A Note on Group Extensions and Proper 3-Realizability.
Mediterranean Journal of Mathematics,
Vol. 13,
Issue. 5,
p.
3303.
Cárdenas, M.
Lasheras, F.F.
Quintero, A.
and
Roy, R.
2020.
A topological equivalence relation for finitely presented groups.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 7,
p.
106300.
Cárdenas, M.
Lasheras, F.F.
and
Quintero, A.
2023.
Weak Z-structures and one-relator groups.
Journal of Pure and Applied Algebra,
Vol. 227,
Issue. 1,
p.
107177.
Cardenas, Manuel
Fernández Lasheras, Francisco
Quintero, Antonio
and
Roy, Ranja
2023.
Proper 2–equivalences between infinite ended
finitely presented groups.
Algebraic & Geometric Topology,
Vol. 23,
Issue. 1,
p.
1.
Lasheras, Francisco F.
and
Mihalik, Michael
2024.
Lifting Semistability in Finitely Generated Ascending HNN-Extensions.
Annales de l'Institut Fourier,
Vol. 74,
Issue. 1,
p.
349.
Cárdenas, M.
Lasheras, F.F.
and
Quintero, A.
2024.
Weak Z-structures for some combinatorial group constructions.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 12,
p.
107761.


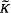 has the proper homotopy type of a (PL) 3-manifold (with boundary).
has the proper homotopy type of a (PL) 3-manifold (with boundary).