Research Article
Height estimates on cubic twists of the Fermat elliptic curve
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-186
-
- Article
-
- You have access
- Export citation
Ascending HNN-extensions and properly 3-realisable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 187-196
-
- Article
-
- You have access
- Export citation
On C*-algebras with the approximate n-th root property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 197-212
-
- Article
-
- You have access
- Export citation
Flat Laguerre planes of Kleinewillinghöfer type E obtained by cut and paste
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-223
-
- Article
-
- You have access
- Export citation
Abstract theory of semiorderings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 225-250
-
- Article
-
- You have access
- Export citation
Finding the group structure of elliptic curves over finite fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 251-263
-
- Article
-
- You have access
- Export citation
On second-order converse duality for a nondifferentiable programming problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 265-270
-
- Article
-
- You have access
- Export citation
Existence of positive solutions for nonlocal and nonvariational elliptic systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-281
-
- Article
-
- You have access
- Export citation
Characterisation of the isometric composition operators on the Bloch space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 283-290
-
- Article
-
- You have access
- Export citation
Bounded vector measures on effect algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-298
-
- Article
-
- You have access
- Export citation
Proper 1-ball contractive retractions in Banach spaces of measurable functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-315
-
- Article
-
- You have access
- Export citation
Complementation of the Jacobson group in a matrix ring
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-324
-
- Article
-
- You have access
- Export citation
Riemann-Siegel sums via stationary phase
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-328
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
On singular Artin monoids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-330
-
- Article
-
- You have access
- Export citation
Poincaré duality pairs of dimensiond three
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-334
-
- Article
-
- You have access
- Export citation
Geometric Seifert 4-manifolds with hyperbolic bases
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 335-336
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 72 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 72 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

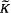
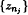 satisfying the conditions
satisfying the conditions 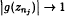 , and
, and
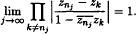
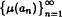 is bounded for each orthogonal sequence {
is bounded for each orthogonal sequence {