Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
LAIZHEN, LUO
and
RONGLU, LI
2008.
MEASURES ON EFFECT ALGEBRAS.
Bulletin of the Australian Mathematical Society,
Vol. 77,
Issue. 3,
p.
433.
Barbieri, Giuseppina
García-Pacheco, Francisco J.
and
Moreno-Pulido, Soledad
2019.
Measures on effect algebras.
Mathematica Slovaca,
Vol. 69,
Issue. 1,
p.
159.
García-Pacheco, Francisco Javier
2022.
The Range of a Module Measure Defined on an Effect Algebra.
Symmetry,
Vol. 14,
Issue. 9,
p.
1819.
García-Pacheco, Francisco Javier
Moreno-Frías, M. A.
and
Murillo-Arcila, Marina
2023.
Topological Ordered Rings and Measures.
Results in Mathematics,
Vol. 78,
Issue. 6,


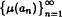 is bounded for each orthogonal sequence {
is bounded for each orthogonal sequence {