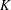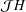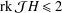Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yan, Dan
and
de Bondt, Michiel
2019.
The classification of some polynomial maps with nilpotent Jacobians.
Linear Algebra and its Applications,
Vol. 565,
Issue. ,
p.
287.
Liu, Dayan
Liu, Fumei
and
Sun, Xiaosong
2021.
Some co-tame automorphisms of affine spaces.
International Journal of Algebra and Computation,
Vol. 31,
Issue. 08,
p.
1601.