Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T00:06:06.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely monotone fading memory relaxation modulii

Published online by Cambridge University Press:  17 April 2009

R. S. Anderssen  and
R. J. Loy
R. S. Anderssen
Affiliation:
CISRO Mathematical and Information Sciences, GPO Box 664, Canberra ACT 2601, Australia
R. J. Loy
Affiliation:
Mathematics Department, School of Mathematical Sciences, Australian National University, Canberra ACT 0200, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In linear viscoelasticity, the fundamental model is the Boltzmann caual integral equation which defines how the stress σ(t) at time t depends on the earlier history of the shear rate 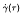via the relaxation modulus (kernel) G (t). Physical reality is achieved by requiring that the form of the relaxation modulus G (t) gives the Boltzmann equation fading memory, so that changes in the distant past have less effect now than the same changes in the more recent past. A popular choice, though others have previously been proposed and investigated, is the assumption that G (t) be a completely monotone function. This assumption has much deeper ramifications than have been identified, discussed or exploited in the rheological literature. The purpose of this paper is to review the key mathematical properties of completely monotone functions, and to illustrate how these properties impact on the theory and application of linear viscoelasticity and polymer dynamics. A more general representation of a completely monotone function, known in the mathematical literature, but not the rheological, is formulated and discussed. This representation is used to derive new rheological relationships. In particular, explicit inversion formulas are derived for the relationships that are obtained when the relaxation spectrum model and a mixing rule are linked through a common relaxation modulus.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 65 , Issue 3 , June 2002 , pp. 449 - 460
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Akyildiz, F., Jones, R.S. and Walters, K., ‘On the spring-dashpot representation of linear viscoelastic behaviour’, Rheol. Acta 29 (1990), 482–484.Google Scholar
[2]Anderssen, R.S. and Loy, R.J., ‘On the scaling of molecular weight distribution functionals’, J. Rheol. 45 (2001), 891–901.CrossRefGoogle Scholar
[3]Anderssen, R.S. and Mead, D.W., ‘Theoretical derivation of molecular weight scaling for rheological parameters’, J. Non-Newtonian Fluid Mech. 76 (1998), 299–306.CrossRefGoogle Scholar
[4]Anderssen, R.S. and Westcott, M., ‘The molecular weight distribution problem and reptation mixing rules’, ANZIAM J. 42 (2000), 26–40.Google Scholar
[5]Beris, A N. and Edwards, B.J., ‘On the admissability criteria for linear viscoelasticity kernels’, Rheol. Acta 32 (1993), 505–510.CrossRefGoogle Scholar
[6]Boltzmann, L., ‘Zur Theorie der elastischen Nachwirkung’, Ann. Phys. Chem. 7 (1876), 624–657.Google Scholar
[7]Day, W. A., ‘On monotonicity of the relaxation functions of viscoelastic materials’, Proc. Camb. Philos. Soc. 67 (1970), 503–508.CrossRefGoogle Scholar
[8]Doss, R., ‘An elementary proof of Titchmarsh's convolution theorem’, Proc. Amer. Math. Soc. 104 (1988), 181–184.Google Scholar
[9]Fabrizo, M. and Morro, A., Mathematical problems in linear viscoelasticity, SIAM Studies in Applied Mathematics 12 (SIAM, Philadelphia, 1992).CrossRefGoogle Scholar
[10]Feller, W., An introduction to probability theory and its applications 2 (John Wiley and Sons, New York, 1971).Google Scholar
[11]Grinshpan, A. Z., Ismail, M.E.H. and Milligan, D.L., ‘Complete monotonicity and diesel fuel spray’, Math. Intelligencer 22 (2000), 43–53.CrossRefGoogle Scholar
[12]Larson, R.G., Constitutive equations for polymer melts and solutions (Butterworths, Boston, 1988).Google Scholar
[13]Léonardi, F., Majesté, J.-C., Allal, A. and Marin, G., ‘Rheological models based on the double reptation mixing rule: The effect of a polydisperse environment’, J. Rheol. 44 (2000), 675–692.CrossRefGoogle Scholar
[14]McLeish, T.C.B. and Larson, R.G., ‘Molecular constitutive equations for a class of branched polymers: The pom-pom polymer’, J. Rheol. 42 (1998), 81–110.CrossRefGoogle Scholar
[15]Mead, D.W., ‘Determination of molecular weight distributions of linear flexible polymers from linear viscoelastic material functions’, J. Rheol. 38 (1994), 1797–1827.Google Scholar
[16]Thimm, W., Friedrich, C., Marth, M. and Honerkamp, J., ‘An analytical relation between relaxation time spectrum and molecular weight distribution’, J. Rheol. 43 (1999), 1663–1672.CrossRefGoogle Scholar
[17]Thimm, W., Friedrich, C., Marth, M. and Honerkamp, J., ‘On the Rouse spectrum and the determination of the molecular weight distribution’, J. Rheol. 44 (2000), 429–438.CrossRefGoogle Scholar
[18]Widder, D.V., The Laplace transform (Princeton University Press, Princeton, 1946).Google Scholar
[19]Wu, S., ‘Characterization of polymer molecular weight distribution by transient viscoelasticity: Polytetrafluoroethylenes’, Poly. Eng. Sci. 28 (1989), 538–543.CrossRefGoogle Scholar