In this paper we first obtain a basic formula for the conditional analytic Feynman integral of the first variation of a functional on Wiener space. We then apply this basic result to obtain several integration by parts formulas for conditional analytic Feynman integrals and conditional Fourier-Feynman transforms.

Are the arc components in a locally compact group Borel subsets? An affirmative answer is provide for locally compact groups satisfying the First Axiom of Count-ability. For general locally compact groups the question is reduced to compact connected Abelian groups. In certain models of set theory the answer is negative.

Let G be a finitely connected domain and let X be a reflexive Banach space of functions analytic on G which admits the multiplication Mz as a polynomially bounded operator. We give some conditions that a sequence in G has an interpolating subsequence for X.

Dedicated to Professor Koichi Ogiue on his sixtieth birthday

We show that the only parallel surfaces in SL (2,ℝ) are rotational surfaces with constant mean curvature.

Banach and Fréchet algebras with a Laurent series generator are investigated leading, via the discrete Beurling algebras, to functional analytic characterisations of the holomorphic function algebras on the annulus as well as the C∞-algebra on the unit circle.

Let α, β γ, δ be complex numbers such that γδ ≠ 0. If A and B are bounded linear operators on the Hilbert space H such that γA + δB is right invertible then we study the operator norm of (αA + βB)(γA + δB)−1 using the angle φ between two subspaces ran A and ran B or the angle ψ = ψ(A, B) between two operators A and B where

Let  be a Banach algebra and let ** be the second dual algebra of  endowed with the first or the second Arens product. We investigate relations between amenability of ** and Arens regularity of  and the rôle topological centres in amenability of **. We also find conditions under which weak amenability of ** implies weak amenability of .

In this paper, we construct a new maximal independent system of units in cyclotomic function fields and their subfields. We also calculate its index in the full units group and show that it is smaller than the index of Feng-Yin's system.

We study the groups of isometries for Hilbert metrics on bounded open convex domains in ℝn and show that if  is such a set with a strictly convex boundary, the Hilbert geometry is asymptotically Riemannian at infinity. As a consequence of this result, we prove there are no Hausdorff quotients of  by isometry subgroups with finite volume except when ∂ is an ellipsoid.

In this paper, for a given Fuchsian group Γ, we prove an upper estimate for the Hausdorff dimension of the radial limit set in the visibility manifold. Further, if Γ is a convex cocompact group, we find the exact Hausdroff dimension of the limit set.

We complete the determination of the groups of positive deficiency which occur as lattices in connected Lie groups. The torsion free groups among them are 3-mainfold groups. We show that any other torsion free 3-manifold group which is such a lattice is the group of an aspherical closed geometric 3-manifold.

We first characterise semi-orthogonal frame wavelets by generalising the characterisation of orthonormal wavelets. We then characterise those semi-orthogonal frame wavelets that are associated with frame multi-resolution analyses. This is a generalisation of a result of Wang and another result of Papadakis. Finally, we illustrate our results by an example.

We prove that for positive integers n and r satisfying 1 < r < n, with the single exception of n = 4 and r = 2, there exists a constant weight Gray code of r-sets of Xn = {1, 2, …, n} that admits an orthogonal labelling by distinct partitions, with each subsequent partition obtained from the previous one by an application of a permutation of the underlying set. Specifically, an r-set A and a partition π of Xn are said to be orthogonal if every class of π meets A in exactly one element. We prove that for all n and r as stated, and 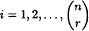taken modulo 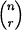, there exists a list 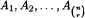of the distinct r-sets of Xn with |Ai ∩ Ai+1| = r − 1 and a list of distinct partitions 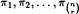such that πi is orthogonal to both Ai and Ai+1, and πi+1 = πiλi for a suitable permutation λi of Xn.

we discuss conditions which ensure that a G-CW complex is G-homotopy equivalent to a CW complex with cellular action with respect to some CW decomposition of the compact Lie group G. For G = SU (2), we prove that for every G-CW complex X, there exists a CW complex Y which is G-homotopy equivalent to X, such that the action G × Y → Y is a cellular map.

Order components of a finite group are introduced in [4]. We prove that, for every q, PSL (5,q) can be uniquely determined by its order componets. A main consequence of our result is the validity of Thompson's conjecture for the groups under consideration.

Two smoothness characterisations of weakly compact sets in Banach spaces are given. One that involves pointwise lower semicontinuous norms and one that involves projectional resolutions of identity.

We give an elementary proof of the statement that a function f on the closed unit ball of Cn, integrable on the unit sphere, is holomorphic if it is invariant under the Bochner–Martinelli integral transform.

The notions of a Baire-1 and a weak Baire-1 multifunction are defined and a striking analogy between Baire-1 multifunctions and classical Baire-1 functions is established. A selection theorem is presented which asserts that if X is a metrisable space, Y a Polish space and F: X → 2Y/{∅} a closed-valued, weak Baire-1 multifunction, then F admits a Baire-1 selection. Using the machinery developed we prove that if X is a Banach space with separable dual, then every weak* usco, defined on a completely metrisable space Z, which values are weakly* compact subsets of the dual, is norm lower semicontinuous on a dense Gδ set.

We prove an explicit Hecke's bound for the Fourier coefficients of holomorphic cusp forms for SL2(Z) and apply it to derive effectively computable constants c (m) for each dimension m, divisible by 8, for which every even integer is always represented by every even unimodular form of m variables.

We give a characterisation for the extension of uniformly smooth norms from subspaces Y of superreflexive spaces X to uniformly smooth norms on all of X. This characterisation is applied to obtain results in various contexts.