Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T21:51:23.415Z Has data issue: false hasContentIssue false
  • English
  • Français

CONGRUENCES MODULO POWERS OF 2 FOR FU’S 5 DOTS BRACELET PARTITIONS

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  22 August 2013

ERNEST X. W. XIA  and
OLIVIA X. M. YAO
ERNEST X. W. XIA
Affiliation:
Department of Mathematics, Jiangsu University, Jiangsu, Zhenjiang 212013, PR China email Ernestxwxia@163.com
OLIVIA X. M. YAO*
Affiliation:
Department of Mathematics, Jiangsu University, Jiangsu, Zhenjiang 212013, PR China email Ernestxwxia@163.com
*
✉yaoxiangmei@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 2007, Andrews and Paule introduced a new class of combinatorial objects called broken 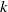$k$-diamond partitions. Recently, Shishuo Fu generalised the notion of broken 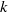$k$-diamond partitions to combinatorial objects which he termed 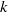$k$ dots bracelet partitions. Fu denoted the number of 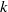$k$ dots bracelet partitions of $n$ by 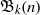${\mathfrak{B}}_{k} (n)$ and proved several congruences modulo primes and modulo powers of 2. More recently, Radu and Sellers extended the set of congruences proven by Fu by proving three congruences modulo squares of primes for 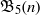${\mathfrak{B}}_{5} (n)$, 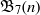${\mathfrak{B}}_{7} (n)$ and 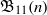${\mathfrak{B}}_{11} (n)$. In this note, we prove some congruences modulo powers of 2 for 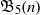${\mathfrak{B}}_{5} (n)$. For example, we find that for all integers 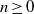$n\geq 0$, 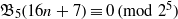${\mathfrak{B}}_{5} (16n+ 7)\equiv 0\hspace{0.167em} ({\rm mod} \hspace{0.334em} {2}^{5} )$.

Keywords

congruences2-dissectionspartitionsk dots bracelet partitions

MSC classification

Secondary: 11P83: Partitions; congruences and congruential restrictions 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 360 - 372
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E. and Paule, P., ‘MacMahon’s partition analysis XI: broken diamonds and modular forms’, Acta Arith. 126 (2007), 281–294.Google Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).CrossRefGoogle Scholar
Calkin, N., Drake, N., James, K., Law, S., Lee, P., Penniston, D. and Radder, J., ‘Divisibility properties of the 5-regular and 13-regular partition functions’, Integers 8 (2008), #A60.Google Scholar
Fu, S., ‘Combinatorial proof of one congruence for the broken 1-diamond partition and a generalization’, Int. J. Number Theory 7 (2011), 133–144.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘On recent congruence results of Andrews and Paule’, Bull. Aust. Math. Soc. 75 (2007), 121–126.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Elementary proofs of parity results for 5-regular partitions’, Bull. Aust. Math. Soc. 81 (2010), 58–63.Google Scholar
Mortenson, E., ‘On the broken 1-diamond partition’, Int. J. Number Theory 4 (2008), 199–218.CrossRefGoogle Scholar
Radu, S. and Sellers, J. A., ‘Congruences modulo squares of primes for Fu’s $k$ dots bracelet partitions’, Int. J. Number Theory 9 (2013), 939–943.CrossRefGoogle Scholar
Sun, Z. H., ‘The expansion of ${ \mathop{\prod }\nolimits}_{k= 1}^{\infty } (1- {q}^{ak} )(1- {q}^{bk} )$’, Acta Arith. 134 (2008), 11–29.CrossRefGoogle Scholar
Xia, E. X. W. and Yao, O. X. M., ‘Some modular relations for the Göllnitz–Gordon functions by an even–odd method’, J. Math. Anal. Appl. 387 (2012), 126–138.CrossRefGoogle Scholar
Xia, E. X. W. and Yao, O. X. M., ‘Analogues of Ramanujan’s partition identities’, Ramanujan J. 31 (2013), 373–396.Google Scholar