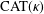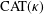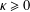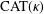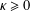Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
CHOI, BYOUNG JIN
2021.
-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN SPACES.
Journal of the Australian Mathematical Society,
Vol. 110,
Issue. 3,
p.
289.