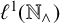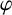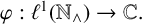1 Introduction and preliminaries
The cohomological notion of amenability was introduced and studied in the pioneering work of Johnson [Reference Johnson5]. A Banach algebra
![]() $\mathcal {A}$
is amenable if every continuous derivation from
$\mathcal {A}$
is amenable if every continuous derivation from
![]() $\mathcal {A}$
into a dual Banach
$\mathcal {A}$
into a dual Banach
![]() $\mathcal {A}$
-bimodule
$\mathcal {A}$
-bimodule
![]() $E^*$
is inner. A modification of amenability depending on multiplicative linear functionals was introduced and studied by Kaniuth et al. [Reference Kaniuth, Lau and Pym6]. A Banach algebra
$E^*$
is inner. A modification of amenability depending on multiplicative linear functionals was introduced and studied by Kaniuth et al. [Reference Kaniuth, Lau and Pym6]. A Banach algebra
![]() $\mathcal {A}$
is called
$\mathcal {A}$
is called
![]() $\varphi $
-amenable if there exists an element m in
$\varphi $
-amenable if there exists an element m in
![]() $\mathcal {A}^{**}$
such that
$\mathcal {A}^{**}$
such that
![]() $m(\varphi )=1$
and
$m(\varphi )=1$
and
![]() $m(f\cdot a)=\varphi (a)m(f)$
for every
$m(f\cdot a)=\varphi (a)m(f)$
for every
![]() $a\in {\mathcal {A}}$
and
$a\in {\mathcal {A}}$
and
![]() $f\in {\mathcal {A}^*}$
, where
$f\in {\mathcal {A}^*}$
, where
![]() $\varphi $
is a multiplicative linear functional on
$\varphi $
is a multiplicative linear functional on
![]() $\mathcal {A}$
. For a locally compact group G, the Fourier algebra
$\mathcal {A}$
. For a locally compact group G, the Fourier algebra
![]() $\mathcal {A}(G)$
is always
$\mathcal {A}(G)$
is always
![]() $\varphi $
-amenable. Moreover, the Segal algebra
$\varphi $
-amenable. Moreover, the Segal algebra
![]() $S^{1}(G)$
is
$S^{1}(G)$
is
![]() $\varphi $
-amenable if and only if G is amenable (see [Reference Alaghmandan, Nasr Isfahani and Nemati1, Reference Kaniuth, Lau and Pym6]).
$\varphi $
-amenable if and only if G is amenable (see [Reference Alaghmandan, Nasr Isfahani and Nemati1, Reference Kaniuth, Lau and Pym6]).
Jaberi and Mahmoodi [Reference Jaberi and Mahmoodi4] introduced the new concept of
![]() $\varphi $
-injectivity for the category of dual Banach algebras, where
$\varphi $
-injectivity for the category of dual Banach algebras, where
![]() $\varphi $
is a
$\varphi $
is a
![]() $wk^*$
-continuous multiplicative linear functional on
$wk^*$
-continuous multiplicative linear functional on
![]() $\mathcal {A}$
. A dual Banach algebra
$\mathcal {A}$
. A dual Banach algebra
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\varphi $
-injective if whenever
$\varphi $
-injective if whenever
![]() $\pi :\mathcal {A}\rightarrow \mathcal {L}(E)$
is a
$\pi :\mathcal {A}\rightarrow \mathcal {L}(E)$
is a
![]() $wk^*$
-continuous unital representation on a reflexive Banach space E, then there is a projection
$wk^*$
-continuous unital representation on a reflexive Banach space E, then there is a projection
![]() $\mathcal {Q}:\mathcal {L}(E)\rightarrow \pi (\mathcal {A})^{\varphi }$
such that
$\mathcal {Q}:\mathcal {L}(E)\rightarrow \pi (\mathcal {A})^{\varphi }$
such that
![]() $\mathcal {Q}(STU)=S\mathcal {Q}(T)U$
for
$\mathcal {Q}(STU)=S\mathcal {Q}(T)U$
for
![]() $S,U\in {\pi (\mathcal {A})^{c}}$
and
$S,U\in {\pi (\mathcal {A})^{c}}$
and
![]() $T\in {\mathcal {L}(E)}$
, where
$T\in {\mathcal {L}(E)}$
, where
![]() $\pi (\mathcal {A})^{\varphi }=\{T\in {\mathcal {L}(E)}:\;\pi (a)T=\varphi (a)T\quad (a\in {\mathcal {A}})\}$
. They proved that
$\pi (\mathcal {A})^{\varphi }=\{T\in {\mathcal {L}(E)}:\;\pi (a)T=\varphi (a)T\quad (a\in {\mathcal {A}})\}$
. They proved that
![]() $\varphi $
-injectivity is equivalent to
$\varphi $
-injectivity is equivalent to
![]() $\varphi $
-amenability [Reference Jaberi and Mahmoodi4, Theorem 3.6].
$\varphi $
-amenability [Reference Jaberi and Mahmoodi4, Theorem 3.6].
There is an important category of dual Banach algebras, called enveloping dual Banach algebras. Let
![]() $\mathcal {A}$
be a Banach algebra and let E be a Banach
$\mathcal {A}$
be a Banach algebra and let E be a Banach
![]() $\mathcal {A}$
-bimodule. An element
$\mathcal {A}$
-bimodule. An element
![]() $x\in {E}$
is called weakly almost periodic if the module maps
$x\in {E}$
is called weakly almost periodic if the module maps
![]() $\mathcal {A}\rightarrow {E}$
given by
$\mathcal {A}\rightarrow {E}$
given by
![]() $a\mapsto {a\cdot {x}}$
and
$a\mapsto {a\cdot {x}}$
and
![]() $a\mapsto {x\cdot {a}}$
are weakly compact. The set of all weakly almost periodic elements of E is denoted by
$a\mapsto {x\cdot {a}}$
are weakly compact. The set of all weakly almost periodic elements of E is denoted by
![]() ${\mathit {WAP}}(E)$
[Reference Runde7, Definition 4.1]. Runde observed that
${\mathit {WAP}}(E)$
[Reference Runde7, Definition 4.1]. Runde observed that
![]() ${\mathit {WAP}}(\mathcal {A}^{\ast })^{\ast }$
is a canonical dual Banach algebra associated to an arbitrary Banach algebra
${\mathit {WAP}}(\mathcal {A}^{\ast })^{\ast }$
is a canonical dual Banach algebra associated to an arbitrary Banach algebra
![]() $\mathcal {A}$
[Reference Runde7, Theorem 4.10]. By means of the new notion of
$\mathcal {A}$
[Reference Runde7, Theorem 4.10]. By means of the new notion of
![]() $\varphi $
-injectivity, Jaberi and Mahmoodi investigated
$\varphi $
-injectivity, Jaberi and Mahmoodi investigated
![]() $\varphi $
-amenability of the enveloping dual Banach algebra
$\varphi $
-amenability of the enveloping dual Banach algebra
![]() ${\mathit {WAP}}(\mathcal {A}^{\ast })^{\ast }$
[Reference Jaberi and Mahmoodi4, Theorem 4.8]. In a short final section of the paper, they claimed that
${\mathit {WAP}}(\mathcal {A}^{\ast })^{\ast }$
[Reference Jaberi and Mahmoodi4, Theorem 4.8]. In a short final section of the paper, they claimed that
![]() ${\mathit {WAP}}(\ell ^1(\mathbb {N}_\wedge )^*)^*$
is not
${\mathit {WAP}}(\ell ^1(\mathbb {N}_\wedge )^*)^*$
is not
![]() $\tilde {\varphi }$
-amenable, where
$\tilde {\varphi }$
-amenable, where
![]() $\tilde {\varphi }$
is the unique extension of the augmentation character
$\tilde {\varphi }$
is the unique extension of the augmentation character
![]() $\varphi $
on the semigroup algebra
$\varphi $
on the semigroup algebra
![]() $\ell ^1(\mathbb {N}_\wedge )$
[Reference Jaberi and Mahmoodi4, Theorem 5.4]. From this result, they concluded that
$\ell ^1(\mathbb {N}_\wedge )$
[Reference Jaberi and Mahmoodi4, Theorem 5.4]. From this result, they concluded that
![]() $\ell ^1(\mathbb {N}_\wedge )$
is not
$\ell ^1(\mathbb {N}_\wedge )$
is not
![]() $\varphi $
-amenable, where
$\varphi $
-amenable, where
![]() $\varphi $
is the augmentation character [Reference Jaberi and Mahmoodi4, Corollary 5.5].
$\varphi $
is the augmentation character [Reference Jaberi and Mahmoodi4, Corollary 5.5].
On the contrary, we show that
![]() $\ell ^1(\mathbb {N}_\wedge )$
is
$\ell ^1(\mathbb {N}_\wedge )$
is
![]() $\varphi $
-amenable for each multiplicative linear functional
$\varphi $
-amenable for each multiplicative linear functional
![]() $\varphi :\ell ^1(\mathbb {N}_\wedge )\rightarrow \mathbb {C}$
and comment on the reason for this counterexample to the result stated in [Reference Jaberi and Mahmoodi4].
$\varphi :\ell ^1(\mathbb {N}_\wedge )\rightarrow \mathbb {C}$
and comment on the reason for this counterexample to the result stated in [Reference Jaberi and Mahmoodi4].
2
 $\varphi $
-amenability of
$\varphi $
-amenability of
 $\ell ^1(\mathbb {N}_\wedge )$
$\ell ^1(\mathbb {N}_\wedge )$
Let
![]() $S=\mathbb {N}$
. With the semigroup product
$S=\mathbb {N}$
. With the semigroup product
![]() $m\wedge n=\min \{m,n\}$
, for
$m\wedge n=\min \{m,n\}$
, for
![]() $m,n\in S$
, the set S becomes a semigroup. It is known that
$m,n\in S$
, the set S becomes a semigroup. It is known that
![]() $\Delta (\ell ^{1}(S))$
consists of all the functions
$\Delta (\ell ^{1}(S))$
consists of all the functions
![]() $\varphi _{n}:\ell ^{1}(S)\rightarrow \mathbb {C}$
given by
$\varphi _{n}:\ell ^{1}(S)\rightarrow \mathbb {C}$
given by
![]() $\varphi _{n}(\sum _{i=1}^{\infty }\alpha _{i}\delta _{i})=\sum _{i=n}^{\infty }\alpha _{i}$
, for
$\varphi _{n}(\sum _{i=1}^{\infty }\alpha _{i}\delta _{i})=\sum _{i=n}^{\infty }\alpha _{i}$
, for
![]() $n\in S$
(see [Reference Dales and Loy2, page 32]). Suppose that
$n\in S$
(see [Reference Dales and Loy2, page 32]). Suppose that
![]() $m=\delta _{1}$
. Then
$m=\delta _{1}$
. Then
![]() $\varphi _{1}(m)=\varphi _{1}(\delta _{1})=1$
and
$\varphi _{1}(m)=\varphi _{1}(\delta _{1})=1$
and
 $$ \begin{align*}am=a\delta_{1}=\bigg(\sum^{\infty}_{i=1}a_{i}\bigg)\delta_{1}=\varphi_{1}(a)\delta_{1}=\varphi_{1}(a)m,\quad\mbox{where } a=\sum^{\infty}_{i=1}a_{i}\delta_{i}\in \ell^{1}(S).\end{align*} $$
$$ \begin{align*}am=a\delta_{1}=\bigg(\sum^{\infty}_{i=1}a_{i}\bigg)\delta_{1}=\varphi_{1}(a)\delta_{1}=\varphi_{1}(a)m,\quad\mbox{where } a=\sum^{\infty}_{i=1}a_{i}\delta_{i}\in \ell^{1}(S).\end{align*} $$
It follows that
![]() $\ell ^{1}(S)$
is
$\ell ^{1}(S)$
is
![]() $\varphi _{1}$
-amenable. For
$\varphi _{1}$
-amenable. For
![]() $n>1$
, define
$n>1$
, define
![]() $m_{n}=\delta _{n}-\delta _{n-1}$
. Then,
$m_{n}=\delta _{n}-\delta _{n-1}$
. Then,
and
 $$ \begin{align*} am_{n}=a(\delta_{n}-\delta_{n-1})=\sum^{\infty}_{i=n}a_{i}(\delta_{n}-\delta_{n-1})=\varphi_{n}(a)(\delta_{n}-\delta_{n-1})=\varphi_{n}(a)m_{n},\end{align*} $$
$$ \begin{align*} am_{n}=a(\delta_{n}-\delta_{n-1})=\sum^{\infty}_{i=n}a_{i}(\delta_{n}-\delta_{n-1})=\varphi_{n}(a)(\delta_{n}-\delta_{n-1})=\varphi_{n}(a)m_{n},\end{align*} $$
where
![]() $ a=\sum ^{\infty }_{i=1}a_{i}\delta _{i}\in \ell ^{1}(S).$
It follows that
$ a=\sum ^{\infty }_{i=1}a_{i}\delta _{i}\in \ell ^{1}(S).$
It follows that
![]() $\ell ^{1}(S)$
is
$\ell ^{1}(S)$
is
![]() $\varphi $
-amenable with respect to each multiplicative linear functional
$\varphi $
-amenable with respect to each multiplicative linear functional
![]() $\varphi :\ell ^{1}(S)\rightarrow \mathbb {C}$
. Thus, [Reference Jaberi and Mahmoodi4, Corollary 5.5] is not true.
$\varphi :\ell ^{1}(S)\rightarrow \mathbb {C}$
. Thus, [Reference Jaberi and Mahmoodi4, Corollary 5.5] is not true.
This counterexample to [Reference Jaberi and Mahmoodi4, Corollary 5.5] shows that [Reference Jaberi and Mahmoodi4, Theorem 5.4] is also not true. The mistake is the assertion in the second sentence of the proof of Theorem 5.4 that ‘there is an isometric isomorphism
![]() $\Theta $
from
$\Theta $
from
![]() $\rho (\ell ^1(\mathbb {N}_{\wedge })^c$
onto
$\rho (\ell ^1(\mathbb {N}_{\wedge })^c$
onto
![]() $\rho (\ell ^{1}(\mathbb {N}_{\wedge }))^ {\varphi }$
’. An example showing that
$\rho (\ell ^{1}(\mathbb {N}_{\wedge }))^ {\varphi }$
’. An example showing that
![]() $\Theta $
cannot be isometric can be constructed using [Reference Daws3, Theorem 7.6]. Take
$\Theta $
cannot be isometric can be constructed using [Reference Daws3, Theorem 7.6]. Take
![]() $\|\sum _{n=1}^\infty a_n\delta _n\| = \sup _{F } \|\sum _{n\in F} a_n\delta _n\|$
, where F is a finite subset of
$\|\sum _{n=1}^\infty a_n\delta _n\| = \sup _{F } \|\sum _{n\in F} a_n\delta _n\|$
, where F is a finite subset of
![]() $\mathbb {N}$
. Take indices
$\mathbb {N}$
. Take indices
![]() $1$
and
$1$
and
![]() $2n+1$
so that the corresponding basis elements belong to distinct summands. Set A to be the diagonal matrix having ones at indices
$2n+1$
so that the corresponding basis elements belong to distinct summands. Set A to be the diagonal matrix having ones at indices
![]() $1$
and
$1$
and
![]() $2n+1$
and zero otherwise. Set B to have ones at indices
$2n+1$
and zero otherwise. Set B to have ones at indices
![]() $1$
and
$1$
and
![]() $2n+1$
in the first row and zeros otherwise. Then
$2n+1$
in the first row and zeros otherwise. Then
![]() $B=\Theta (A)$
and
$B=\Theta (A)$
and
 $$ \begin{align*} \|A\| & = \sup\bigg\{\|a_1\delta_n+a_{2n+1}\delta_{2n+1}\| : \bigg\|\sum a_n\delta_n\bigg\|=1\bigg\} \\ & = \sum\{(a_1^2+a_{2n+1}^2)^{1/2} : (a_1^2+a_{2n+1}^2)^{1/2}=1\} = 1, \end{align*} $$
$$ \begin{align*} \|A\| & = \sup\bigg\{\|a_1\delta_n+a_{2n+1}\delta_{2n+1}\| : \bigg\|\sum a_n\delta_n\bigg\|=1\bigg\} \\ & = \sum\{(a_1^2+a_{2n+1}^2)^{1/2} : (a_1^2+a_{2n+1}^2)^{1/2}=1\} = 1, \end{align*} $$
while
 $$ \begin{align*} \|B\| &= \sup\bigg\{|a_1+a_{2n+1}| : \bigg\|\sum a_n\delta_n\bigg\|=1\bigg\} \\ &= \sum\{|a_1+a_{2n+1}| : (a_1^2+a_{2n+1}^2)^{1/2}=1\} = \sqrt{2}. \end{align*} $$
$$ \begin{align*} \|B\| &= \sup\bigg\{|a_1+a_{2n+1}| : \bigg\|\sum a_n\delta_n\bigg\|=1\bigg\} \\ &= \sum\{|a_1+a_{2n+1}| : (a_1^2+a_{2n+1}^2)^{1/2}=1\} = \sqrt{2}. \end{align*} $$
Consequently,
![]() $\Theta $
is not isometric. By taking k summands in a similar way, it can be shown that
$\Theta $
is not isometric. By taking k summands in a similar way, it can be shown that
![]() $\Theta $
is unbounded on diagonal elements of finite support.
$\Theta $
is unbounded on diagonal elements of finite support.
Acknowledgements
The authors would like to thank the anonymous referee for very careful reading and valuable comments that improved the presentation of the manuscript and pinpointed the error in [Reference Jaberi and Mahmoodi4]. Also the first author thanks Ilam university for its support.