Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-27T17:18:49.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential inclusions and abstract control problems

Published online by Cambridge University Press:  17 April 2009

Mieczyław Cichoń
Mieczyław Cichoń
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Matejki 48/4960–769 PoznańPoland e-mail: mcichon@math.amu.edu.plmcichon@plpuam11.bitnet
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

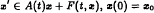We prove an existence theorem for differential inclusions in Banach spaces. Here {A (t): t ∈ [0,T]} is a family of linear operators generating a continuous evolution operator K (t, s). We concentrate on maps F with F (t,·) weakly sequentially hemi-continuous.

Moreover, we show a compactness of the set of all integral solutions of the above problem. These results are also applied to a semilinear optimal control problem. Some corollaries, important in the theory of optimal control, are given too. We extend in several ways theorems existing in the literature.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 53 , Issue 1 , February 1996 , pp. 109 - 122
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Aubin, J.-P. and Cellina, A., Differential inclusions (Springer-Verlag, Berlin, Heidelberg, New York, 1984).CrossRefGoogle Scholar
[2]Aubin, J.-P. and Ekeland, I., Applied nonlinear analysis (J. Wiley, New York, 1984).Google Scholar
[3]Aubin, J.-P. and Frankowska, H., Set-Valued Analysis (Birkhäuser, Boston, Basel, Berlin, 1990).Google Scholar
[4]Banaś, J. and Goebel, K., Measures of noncompactness in Banach spaces, Lecture Notes in Pure Applied Math. 60 (Marcel Dekker Inc., New York, Basel, 1980).Google Scholar
[5]Cannarsa, P. and Frankowska, H., ‘Value functions and optimality conditions for semilinear control problem’, Appl. Math. Optim. (to appear).Google Scholar
[6]Cannarsa, P. and Frankowska, H., ‘Value functions and optimality conditions for semilinear control problems II: Parabolic case’, IIASA WP-91–32 (1991).Google Scholar
[7]Castaing, C. and Valadier, M., Convex analysis and measurable multifunctions, Lecture Notes Math. 580 (Springer-Verlag, Berlin, Heidelberg, New York, 1977).CrossRefGoogle Scholar
[8]Cichoń, M., ‘A point of view on measures of noncompactness’, Demonstratio Math. 26 (1993), 767–777.Google Scholar
[9]Cichoń, M., ‘On measures of weak noncompactness’, Publ. Math. Debrecen 45 (1994), 93–102.Google Scholar
[10]DeBlasi, F. S., ‘On a property of the unit sphere in a Banach space’, Bull. Math. Soc. Sci. Math. R. S. Roumanie 21 (1977), 259–262.Google Scholar
[11]Deimling, K., ‘Multivalued differential equations with use right-hand side’, in Proc. Int. Conf. Theory and Applic. of Diff. Eqs I, (Aftabizadeh, R., Editor) (Ohio Unviersity Press, Athens, 1989), pp. 217–222.Google Scholar
[12]Deimling, K., Multivalued differential equations (Walter de Gruyter, Berlin, New York, 1992).Google Scholar
[13]Deimling, K. and Rao, M., ‘On solution sets of multivalued differential equations’, Appl. Anal. 30 (1988), 129–135.Google Scholar
[14]Frankowska, H., ‘A priori estimates for operational differential inclusions’, J. Differential Equations 84 (1990), 100–128.CrossRefGoogle Scholar
[15]Frankowska, H., Control of nonlinear systems and differential inclusions, (in press).Google Scholar
[16]Hess, C., ‘Measurability and integrability of the weak upper limit of a sequence of multi-functions’, J. Math. Anal. Appl. 153 (1990), 226–249.Google Scholar
[17]Kato, T., Perturbation theory for linear operators (Springer-Verlag, Berlin, Heidelberg, New York, 1966).Google Scholar
[18]Kisielewicz, M., Differential inclusions and optimal control (PWN - Polish Scientific Publishers/Kluwer Academic Publishers, Warsaw, London, 1991).Google Scholar
[19]Papageorgiou, N.S., ‘On the attainable set of differential inclusions and control systems’, J. Math. Anal. Appl. 125 (1987), 305–322.CrossRefGoogle Scholar
[20]Papageorgiou, N.S., ‘On multivalued evolution equations and differential inclusions in Banach spaces’, Comment. Math. Univ. Sancti Pauli 36 (1987), 21–39.Google Scholar
[21]Papageorgiou, N.S., ‘On multivalued semilinear evolution equations’, Boll. Un. Mat. Ital. B 3 (1989), 1–16.Google Scholar
[22]Rolewicz, S., Functional analysis and control theory (PWN - Polish Scientific Publishers/D. Reidel Publ., Warsaw, Dordrecht, 1987).Google Scholar
[23]Shih, M.S. and Tan, K.K., ‘Covering theorems of convex sets related to fixed point theorems’, in Nonlinear and convex analysis Proceedings in honor of Ky Fan, (Lin, B.L. and Simon, S., Editors), Lecture Notes in Pure Applied Math. 107 (Marcel Dekker Inc., New York Basel, 1987), pp. 235–244.Google Scholar
[24]Ülger, A., ‘Weak compactness in L 1(μ,X)’, Proc. Amer. Math. Soc. 113 (1991), 143–149.Google Scholar
[25]Vrabie, I.I., Compactness methods for nonlinear evolutions, Pitman Monograph and Surveys in Pure and Applied Mathematics 32 (Longman, Boston, 1987).Google Scholar
[26]Tolstonogov, A. A., Differential inclusions in a Banach space, (in Russian) (Izd. “Nauka”, Moscow, 1986).Google Scholar