Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T21:39:35.306Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPANSION OF ORBITS OF SOME DYNAMICAL SYSTEMS OVER FINITE FIELDS

Part of: Elementary number theory Ergodic theory Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  07 April 2010

JAIME GUTIERREZ  and
IGOR E. SHPARLINSKI
JAIME GUTIERREZ
Affiliation:
Department of Applied Mathematics and Computer Science, University of Cantabria, E-39071 Santander, Spain (email: jaime.gutierrez@unican.es)
IGOR E. SHPARLINSKI*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia (email: igor@comp.mq.edu.au)
*
✉For correspondence; e-mail: igor@comp.mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a finite field 𝔽p={0,…,p−1} of p elements, where p is a prime, we consider the distribution of elements in the orbits of a transformation ξ↦ψ(ξ) associated with a rational function ψ∈𝔽p(X). We use bounds of exponential sums to show that if N≥p1/2+ε for some fixed ε then no N distinct consecutive elements of such an orbit are contained in any short interval, improving the trivial lower bound N on the length of such intervals. In the case of linear fractional functions 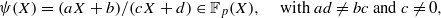we use a different approach, based on some results of additive combinatorics due to Bourgain, that gives a nontrivial lower bound for essentially any admissible value of N.

Keywords

dynamical systemsorbitsexponential sumsadditive combinatorics

MSC classification

Secondary: 11A07: Congruences; primitive roots; residue systems 37A45: Relations with number theory and harmonic analysis 37P05: Polynomial and rational maps
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 82 , Issue 2 , October 2010 , pp. 232 - 239
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

Footnotes

During the preparation of this paper, the first author was supported in part by Spain Ministry of Education and Science Grant MTM2007-67088 and the second author by the Australian Research Council Grant DP0556431.

References

[1]Bourgain, J., ‘More on the sum–product phenomenon in prime fields and its applications’, Int. J. Number Theory 1 (2005), 1–32.CrossRefGoogle Scholar
[2]Bourgain, J., ‘Multilinear exponential sums in prime fields under optimal entropy condition on the sources’, Geom. Funct. Anal. 18 (2009), 1477–1502.CrossRefGoogle Scholar
[3]Bourgain, J. and Garaev, M. Z., ‘On a variant of sum-product estimates and explicit exponential sum bounds in prime fields’, Math. Proc. Camb. Phil. Soc. 146 (2008), 1–21.Google Scholar
[4]Chan, T. H. and Shparlinski, I. E., On the concentration of points on modular hyperbolas and exponential curves, Acta Arith., to appear.Google Scholar
[5]Drmota, M. and Tichy, R., Sequences, Discrepancies and Applications (Springer, Berlin, 1997).Google Scholar
[6]Konyagin, S. V., ‘Bounds of exponential sums over subgroups and Gauss sums’, Proc. 4th Int. Conf. Modern Problems of Number Theory and its Applications (Moscow Lomonosov State University, Moscow, 2002), pp. 86–114 (in Russian).Google Scholar
[7]Konyagin, S. V. and Shparlinski, I. E., Character Sums with Exponential Functions and their Applications (Cambridge University Press, Cambridge, 1999).Google Scholar
[8]Korobov, N. M., Exponential Sums and their Applications (Kluwer, Dordrecht, 1992).Google Scholar
[9]Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (Wiley-Interscience, New York, 1974).Google Scholar
[10]Moreno, C. J. and Moreno, O., ‘Exponential sums and Goppa codes I’, Proc. Amer. Math. Soc. 111 (1991), 523–531.Google Scholar