Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T18:42:17.766Z Has data issue: false hasContentIssue false
  • English
  • Français

FEW-WEIGHT CODES FROM TRACE CODES OVER 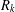$R_{k}$

Part of: Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  03 May 2018

MINJIA SHI ,
YUE GUAN ,
CHENCHEN WANG  and
PATRICK SOLÉ
MINJIA SHI*
Affiliation:
Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Anhui University, No. 3 Feixi Road, Hefei, Anhui Province 230039, PR China School of Mathematical Sciences, Anhui University, Hefei, Anhui, 230601, PR China email smjwcl.good@163.com
YUE GUAN
Affiliation:
School of Mathematical Sciences, Anhui University, Hefei, Anhui, 230601, PR China email guanyueeee@163.com
CHENCHEN WANG
Affiliation:
School of Mathematical Sciences, Anhui University, Hefei, Anhui, 230601, PR China email wangchenchen233@163.com
PATRICK SOLÉ
Affiliation:
CNRS/LAGA, Université Paris 8, 93 526 Saint-Denis, France email sole@enst.fr
*
✉ smjwcl.good@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct two families of few-weight codes for the Lee weight over the ring 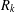$R_{k}$ based on two different defining sets. For the first defining set, taking the Gray map, we obtain an infinite family of binary two-weight codes which are in fact 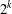$2^{k}$ -fold replicated MacDonald codes. For the second defining set, we obtain two infinite families of few-weight codes. These few-weight codes can be used to implement secret-sharing schemes.

Keywords

few-weights codestrace codesGray maydefining set

MSC classification

Primary: 94B05: Linear codes, general
Secondary: 94B15: Cyclic codes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 167 - 174
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This research is supported by the National Natural Science Foundation of China (61672036), Excellent Youth Foundation of Natural Science Foundation of Anhui Province (1808085J20), Technology Foundation for Selected Overseas Chinese Scholar, Ministry of Personnel of China (05015133) and Key projects of support program for outstanding young talents in Colleges and Universities (gxyqZD2016008).

References

Ashikhmin, A. and Barg, A., ‘Minimal vectors in linear codes’, IEEE Trans. Inform. Theory 44 (1998), 2010–2017.Google Scholar
Calderbank, R. and Kantor, W. M., ‘The geometry of two-weight codes’, Bull. Lond. Math. Soc. 18 (1986), 97–122.Google Scholar
Carlet, C., ‘Boolean functions for cryptography and error correcting codes’, in: Boolean Models and Methods in Mathematics, Computer Science, and Engineering (eds. Crama, Yves and Hammer, P. L.) (Cambridge University Press, New York, 2010), 257–397.Google Scholar
Delsarte, P., ‘Weights of linear codes and strongly regular normed spaces’, Discrete Math. 3 (1972), 47–64.Google Scholar
Ding, C. and Yuan, J., ‘Covering and secret sharing with linear codes’, Springer LNCS 2731 (2003), 11–25.Google Scholar
Ding, K. and Ding, C., ‘A class of two-weight and three-weight codes and their applications in secret sharing’, IEEE Trans. Inform. Theory 61 (2015), 5835–5842.Google Scholar
Dougherty, S. T., Yildiz, B. and Karadeniz, S., ‘Codes over R k , Gray maps and their binary images’, Finite Fields Appl. 17 (2011), 205–219.CrossRefGoogle Scholar
Heng, Z. and Yue, Q., ‘A class of binary linear codes with at most three weights’, IEEE Commun. Lett. 19 (2015), 1488–1491.Google Scholar
Heng, Z. and Yue, Q., ‘A class of $q$ -ary linear codes derived from irreducible cyclic codes’, Preprint, 2015, arXiv:1511.09174vl.Google Scholar
MacDonald, J. E., ‘Design methods for maximum minimum-distance error-correcting codes’, IBM J. Res. Develop. 4 (1960), 43–57.Google Scholar
MacWilliams, F. J. and Sloane, N. J. A., The Theory of Error-Correcting Codes (North-Holland, Amsterdam, 1977).Google Scholar
Massey, J. L., ‘Minimal codewords and secret sharing’, in: Proc. 6th Joint Swedish-Russian Workshop on Information Theory, Mölle, Sweden (Institutionen for informationsteori, Tekniska hogsk., Lund, Sweden, 1993), 276–279.Google Scholar
Shi, M., Guan, Y. and Solé, P., ‘Two new families of two-weight codes’, IEEE Trans. Inform. Theory 63 (2017), 6240–6246.Google Scholar
Shi, M., Liu, Y. and Solé, P., ‘Optimal two-weight codes from trace codes over F2 + uF2 ’, IEEE Commun. Lett. 20 (2016), 2346–2349.CrossRefGoogle Scholar
Shi, M., Liu, Y. and Solé, P., ‘Optimal binary codes from trace codes over a non-chain ring’, Discrete Appl. Math. 219 (2017), 176–181.Google Scholar