Article contents
INDECOMPOSABLE REPRESENTATIONS OF THE EUCLIDEAN ALGEBRA 𝔢(3) FROM IRREDUCIBLE REPRESENTATIONS OF 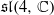
Published online by Cambridge University Press: 01 April 2011
Abstract
The Euclidean group E(3) is the noncompact, semidirect product group E(3)≅ℝ3⋊SO(3). It is the Lie group of orientation-preserving isometries of three-dimensional Euclidean space. The Euclidean algebra 𝔢(3) is the complexification of the Lie algebra of E(3). We embed the Euclidean algebra 𝔢(3) into the simple Lie algebra 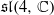 and show that the irreducible representations V (m,0,0) and V (0,0,m) of
and show that the irreducible representations V (m,0,0) and V (0,0,m) of 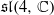 are 𝔢(3)-indecomposable, thus creating a new class of indecomposable 𝔢(3) -modules. We then show that V (0,m,0) may decompose.
are 𝔢(3)-indecomposable, thus creating a new class of indecomposable 𝔢(3) -modules. We then show that V (0,m,0) may decompose.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Publishing Association Inc. 2011
Footnotes
The work of A.D. is partially supported by the Professional Staff Congress/City University of New York (PSC/CUNY). The work of J.R. is partially supported by the Natural Sciences and Engineering Research Council (NSERC).
References
- 8
- Cited by


