Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-13T06:27:19.351Z Has data issue: false hasContentIssue false
  • English
  • Français

ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  08 June 2017

XIAOYOU CHEN  and
MARK L. LEWIS Open the ORCID record for MARK L. LEWIS [Opens in a new window]
XIAOYOU CHEN
Affiliation:
College of Science, Henan University of Technology, Zhengzhou 450001, China email cxymathematics@hotmail.com
MARK L. LEWIS*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, USA email lewis@math.kent.edu
*
✉lewis@math.kent.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 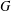$G$ be a finite solvable group and let 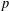$p$ be a prime. In this note, we prove that 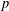$p$ does not divide 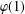$\unicode[STIX]{x1D711}(1)$ for every irreducible monomial 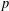$p$-Brauer character 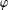$\unicode[STIX]{x1D711}$ of 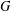$G$ if and only if 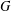$G$ has a normal Sylow 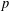$p$-subgroup.

Keywords

solvable groupItô’s theoremmonomial p-Brauer character

MSC classification

Primary: 20C20: Modular representations and characters
Secondary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 426 - 428
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by the China Scholarship Council, Funds of Henan University of Technology (2014JCYJ14, 2016JJSB074, 26510009), Project of Department of Education of Henan Province (17A110004), Projects of Zheng-zhou Municipal Bureau of Science and Technology (20150249, 20140970) and the NSFC (11571129).

References

Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Navarro, G., Characters and Blocks of Finite Groups (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Pang, L. and Lu, J., ‘Finite groups and degrees of irreducible monomial characters’, J. Algebra Appl. 15 (2016), 1650073, 4 pages.CrossRefGoogle Scholar