No CrossRef data available.
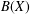 $B(X)$
$B(X)$Published online by Cambridge University Press: 01 March 2016
We focus on a question raised by Daws [‘Arens regularity of the algebra of operators on a Banach space’, Bull. Lond. Math. Soc.36 (2004), 493–503] concerning the Arens regularity of 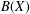 $B(X)$, the algebra of operators on a Banach space
$B(X)$, the algebra of operators on a Banach space  $X$. Among other things, we show that
$X$. Among other things, we show that  $B(X)$ is Arens regular if and only if
$B(X)$ is Arens regular if and only if 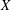 $X$ is ultrareflexive.
$X$ is ultrareflexive.