Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shield, David
1972.
Bounds on the Engel class of some group extensions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 71,
Issue. 2,
p.
179.
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.

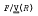 the answer is “yes” for the stronger properties considered, but for the weaker ones the question remains open.
the answer is “yes” for the stronger properties considered, but for the weaker ones the question remains open.