Given a self adjoint operator, T, on a Hilbert space H, and given an integer n ≥ 1, we produce a collection 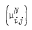 , N ∈ L, of n × n positive matrix measures and a unitary map U:
, N ∈ L, of n × n positive matrix measures and a unitary map U: 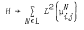 such that UTU−1, restricted to the co-ordinate space
such that UTU−1, restricted to the co-ordinate space 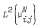 , is the multiplication operator F(t) → tF(t) in that space. This is a generalization of the spectral representation theory of Dunford and Schwartz, Linear operators, II (1966).
, is the multiplication operator F(t) → tF(t) in that space. This is a generalization of the spectral representation theory of Dunford and Schwartz, Linear operators, II (1966).