Article contents
ON A PROBLEM OF ERDŐS ABOUT GRAPHS WHOSE SIZE IS THE TURÁN NUMBER PLUS ONE
Published online by Cambridge University Press: 24 May 2021
Abstract
We consider finite simple graphs. Given a graph H and a positive integer 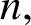 $n,$
the Turán number of H for the order
$n,$
the Turán number of H for the order 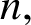 $n,$
denoted
$n,$
denoted 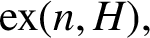 $\mathrm {ex}(n,H),$
is the maximum size of a graph of order n not containing H as a subgraph. Erdős asked: ‘For which graphs H is it true that every graph on n vertices and
$\mathrm {ex}(n,H),$
is the maximum size of a graph of order n not containing H as a subgraph. Erdős asked: ‘For which graphs H is it true that every graph on n vertices and 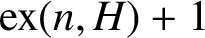 $\mathrm {ex}(n,H)+1$
edges contains at least two H’s? Perhaps this is always true.’ We solve this problem in the negative by proving that for every integer
$\mathrm {ex}(n,H)+1$
edges contains at least two H’s? Perhaps this is always true.’ We solve this problem in the negative by proving that for every integer 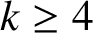 $k\ge 4$
there exists a graph H of order k and at least two orders n such that there exists a graph of order n and size
$k\ge 4$
there exists a graph H of order k and at least two orders n such that there exists a graph of order n and size 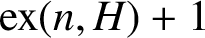 $\mathrm {ex}(n,H)+1$
which contains exactly one copy of
$\mathrm {ex}(n,H)+1$
which contains exactly one copy of 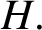 $H.$
Denote by
$H.$
Denote by  $C_4$
the
$C_4$
the 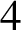 $4$
-cycle. We also prove that for every integer n with
$4$
-cycle. We also prove that for every integer n with 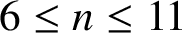 $6\le n\le 11$
there exists a graph of order n and size
$6\le n\le 11$
there exists a graph of order n and size 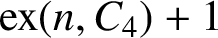 $\mathrm {ex}(n,C_4)+1$
which contains exactly one copy of
$\mathrm {ex}(n,C_4)+1$
which contains exactly one copy of 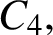 $C_4,$
but, for
$C_4,$
but, for 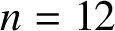 $n=12$
or
$n=12$
or 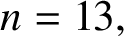 $n=13,$
the minimum number of copies of
$n=13,$
the minimum number of copies of  $C_4$
in a graph of order n and size
$C_4$
in a graph of order n and size 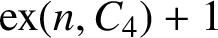 $\mathrm {ex}(n,C_4)+1$
is two.
$\mathrm {ex}(n,C_4)+1$
is two.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by the NSFC grants 11671148 and 11771148 and Science and Technology Commission of Shanghai Municipality (STCSM) grant 18dz2271000.
References
- 2
- Cited by



