Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T06:00:15.234Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GROUPS WITH FINITE CONJUGACY CLASSES IN A VERBAL SUBGROUP

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  08 June 2017

COSTANTINO DELIZIA ,
PAVEL SHUMYATSKY  and
ANTONIO TORTORA Open the ORCID record for ANTONIO TORTORA [Opens in a new window]
COSTANTINO DELIZIA
Affiliation:
Dipartimento di Matematica, Università di Salerno, Via Giovanni Paolo II, 132 - 84084 - Fisciano (SA), Italy email cdelizia@unisa.it
PAVEL SHUMYATSKY
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia-DF, 70910-900, Brazil email pavel@unb.br
ANTONIO TORTORA*
Affiliation:
Dipartimento di Matematica, Università di Salerno, Via Giovanni Paolo II, 132 - 84084 - Fisciano (SA), Italy email antortora@unisa.it
*
✉antortora@unisa.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 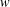$w$ be a group-word. For a group 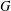$G$, let 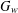$G_{w}$ denote the set of all $w$-values in 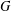$G$ and let 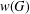$w(G)$ denote the verbal subgroup of 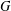$G$ corresponding to 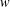$w$. The group 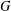$G$ is an 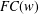$FC(w)$-group if the set of conjugates 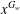$x^{G_{w}}$ is finite for all 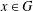$x\in G$. It is known that if 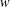$w$ is a concise word, then 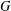$G$ is an 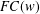$FC(w)$-group if and only if 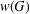$w(G)$ is 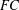$FC$-embedded in 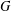$G$, that is, the conjugacy class 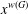$x^{w(G)}$ is finite for all 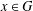$x\in G$. There are examples showing that this is no longer true if 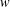$w$ is not concise. In the present paper, for an arbitrary word 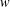$w$, we show that if 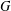$G$ is an 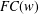$FC(w)$-group, then the commutator subgroup 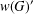$w(G)^{\prime }$ is 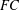$FC$-embedded in 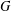$G$. We also establish the analogous result for 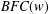$BFC(w)$-groups, that is, groups in which the sets 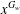$x^{G_{w}}$ are boundedly finite.

Keywords

conjugacy classFC-groupverbal subgroup

MSC classification

Primary: 20E45: Conjugacy classes
Secondary: 20F24: FC-groups and their generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 429 - 437
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author was supported by the ‘National Group for Algebraic and Geometric Structures and their Applications’ (GNSAGA – INdAM) and FAPDF-Brazil.

References

Brazil, S., Krasilnikov, A. and Shumyatsky, P., ‘Groups with bounded verbal conjugacy classes’, J. Group Theory 9(1) (2006), 127–137.Google Scholar
Fernández-Alcober, G. A. and Morigi, M., ‘Outer commutator words are uniformly concise’, J. Lond. Math. Soc. (2) 82(3) (2010), 581–595.CrossRefGoogle Scholar
Fernández-Alcober, G. A., Morigi, M. and Traustason, G., ‘A note on conciseness of Engel words’, Comm. Algebra 40(7) (2012), 2570–2576.Google Scholar
Franciosi, S., de Giovanni, F. and Shumyatsky, P., ‘On groups with finite verbal conjugacy classes’, Houston J. Math. 28(4) (2002), 683–689.Google Scholar
Guralnick, R. M. and Maróti, A., ‘Average dimension of fixed point spaces with applications’, Adv. Math. 226(1) (2011), 298–308.Google Scholar
Neumann, B. H., ‘Groups with finite classes of conjugate elements’, Proc. Lond. Math. Soc. (3) 1 (1951), 178–187.Google Scholar
Neumann, P. M. and Vaughan-Lee, M. R., ‘An essay on BFC groups’, Proc. Lond. Math. Soc. (3) 35(2) (1977), 213–237.CrossRefGoogle Scholar
Robinson, D. J. R., Finiteness Conditions and Generalized Soluble Groups, Part 1 (Springer, New York, Berlin, 1972).Google Scholar
Segal, D. and Shalev, A., ‘On groups with bounded conjugacy classes’, Quart. J. Math. Oxford Ser. (2) 50 (1999), 505–516.Google Scholar
Wiegold, J., ‘Groups with boundedly finite classes of conjugate elements’, Proc. R. Soc. Lond. A 238 (1957), 389–401.Google Scholar