Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bor, Hüseyin
1994.
On absolute summability factors of infinite series.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 104,
Issue. 2,
Savaş, Ekrem
2009.
A summability factor theorem for absolute summability involving quasi-monotone sequences.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 6,
p.
2442.
ÖZARSLAN, Hikmet Seyhan
and
ŞAKAR, Mehmet Öner
2015.
A NEW APPLICATION OF ABSOLUTE MATRIX SUMMABILITY.
Mathematical Sciences and Applications E-Notes,
Vol. 3,
Issue. 1,
p.
36.
Özarslan, Hikmet Seyhan
2016.
Current Topics in Summability Theory and Applications.
p.
313.
Bor, Hüseyin
2018.
An application of quasi-monotone sequences to infinite series and Fourier series.
Analysis and Mathematical Physics,
Vol. 8,
Issue. 1,
p.
77.
Yildiz, Sebnem
2018.
A matrix application of quasi-monotone sequences to infinite series and Fourier series.
Vol. 1978,
Issue. ,
p.
380003.
Yıldız, Şebnem
2021.
On absolute matrix summability factors of infinite series and Fourier series.
Bulletin des Sciences Mathématiques,
Vol. 170,
Issue. ,
p.
103000.
Bor, Hüseyin
2021.
Factored infinite series and Fourier series involving almost increasing sequences.
Bulletin des Sciences Mathématiques,
Vol. 169,
Issue. ,
p.
102990.
Bor, Hüseyin
2022.
Absolute weighted arithmetic mean summability of factored infinite series and Fourier series.
Bulletin des Sciences Mathématiques,
Vol. 176,
Issue. ,
p.
103116.
Özarslan, H. S.
and
Şakar, M. Ö.
2022.
A New Application of (ϕ,δ)-Monotone Sequences.
Russian Mathematics,
Vol. 66,
Issue. 3,
p.
30.


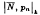 summability factors of infinite series, which generalises a theorem of Mazhar [7] on |
summability factors of infinite series, which generalises a theorem of Mazhar [7] on |