Research Article
A generalised exchange theorem for matroid bases
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-180
-
- Article
-
- You have access
- Export citation
A law of the iterated logarithm for martingales
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-185
-
- Article
-
- You have access
- Export citation
On quasi-monotone sequences and their applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 187-192
-
- Article
-
- You have access
- Export citation
Lefschetz numbers and unitary groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-209
-
- Article
-
- You have access
- Export citation
Existence of optimal controls for a class of nonlinear distributed parameter systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-224
-
- Article
-
- You have access
- Export citation
Hyperbolic flows are topologically stable
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 225-232
-
- Article
-
- You have access
- Export citation
A note on universally zero-divisor rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-239
-
- Article
-
- You have access
- Export citation
On the p-norm of the truncated n-dimensional Hilbert transform
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-250
-
- Article
-
- You have access
- Export citation
Projective submersions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 251-256
-
- Article
-
- You have access
- Export citation
Automorphisms of directed triple systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 257-264
-
- Article
-
- You have access
- Export citation
A characterisation result for matrix rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 265-267
-
- Article
-
- You have access
- Export citation
A property of subgroups of free groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 269-272
-
- Article
-
- You have access
- Export citation
On moment conditions for supremum of normed sums of martingale differences
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-277
-
- Article
-
- You have access
- Export citation
On weak spectral synthesis
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-282
-
- Article
-
- You have access
- Export citation
A theorem of Archimedes about spheres and cylinders and two-point homogeneous spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 283-294
-
- Article
-
- You have access
- Export citation
Approximation in function modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 295-302
-
- Article
-
- You have access
- Export citation
Open images of compactifications of the ray
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 303-306
-
- Article
-
- You have access
- Export citation
An identity involving Nörlund polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-315
-
- Article
-
- You have access
- Export citation
Some inequalities on quasi-subordinate functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-324
-
- Article
-
- You have access
- Export citation
On the generators of S-unit groups in algebraic number fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-329
-
- Article
-
- You have access
- Export citation

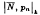 summability factors of infinite series, which generalises a theorem of Mazhar [7] on |
summability factors of infinite series, which generalises a theorem of Mazhar [7] on |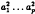 , or that
, or that