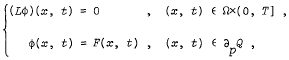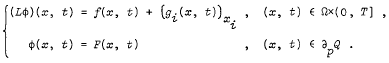Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nababan, S.
and
Teo, K. L.
1979.
On the system governed by parabolic partial delay-differential equations with first boundary conditions.
Annali di Matematica Pura ed Applicata,
Vol. 121,
Issue. 1,
p.
39.