Research Article
Centralizers involving Mathieu groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-323
-
- Article
-
- You have access
- Export citation
The freeness of some projective metabelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-167
-
- Article
-
- You have access
- Export citation
Presentations of some classical groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-12
-
- Article
-
- You have access
- Export citation
A comparison theorem and the forced oscillation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 13-19
-
- Article
-
- You have access
- Export citation
Fuzzy machines in a category
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-210
-
- Article
-
- You have access
- Export citation
Geometric properties of the norm and basic sequences in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-335
-
- Article
-
- You have access
- Export citation
Maximal sum-free sets in finite abelian groups, V
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-342
-
- Article
-
- You have access
- Export citation
The regularity series of a convergence space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-44
-
- Article
-
- You have access
- Export citation
On the Sylow subgroups of a doubly transitive permutation group III
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-240
-
- Article
-
- You have access
- Export citation
Nonexistence of certain supplementary difference sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 343-348
-
- Article
-
- You have access
- Export citation
Some fixed-point theorems on locally convex linear topological spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-254
-
- Article
-
- You have access
- Export citation
Martingale central limit theorems without uniform asymptotic negligibility
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-55
-
- Article
-
- You have access
- Export citation
On semi-simple radical classes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 349-353
-
- Article
-
- You have access
- Export citation
Special morphisms for zero-set spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 57-68
-
- Article
-
- You have access
- Export citation
Oscillatory behaviour of an equation arising from an industrial problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-260
-
- Article
-
- You have access
- Export citation
A question of Babai on groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 355-368
-
- Article
-
- You have access
- Export citation
On smoothness of the Banach space embedding
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 69-74
-
- Article
-
- You have access
- Export citation
On common fixed points for a family of mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 261-267
-
- Article
-
- You have access
- Export citation
Nonstandard topological extensions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 269-290
-
- Article
-
- You have access
- Export citation
Equationally complete varieties of generalized groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 75-83
-
- Article
-
- You have access
- Export citation

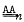 has been answered in the affirmative for
has been answered in the affirmative for 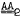 is free. If
is free. If 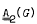 , then the group
, then the group 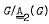 -module
-module 
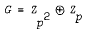 by Yap. We now prove this conjecture for groups
by Yap. We now prove this conjecture for groups 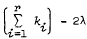 is the sum of
is the sum of