Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brunner, A. M.
Burns, R. G.
and
Oates-Williams, Sheila
1993.
On Almost Primitive Elements of Free Groups With an Application to Fuchsian Groups.
Canadian Journal of Mathematics,
Vol. 45,
Issue. 2,
p.
225.
Comerford, Leo P.
1995.
Generic elements of free groups.
Archiv der Mathematik,
Vol. 65,
Issue. 3,
p.
185.
Stallings, John R.
1995.
Geometric Group Theory.
p.
165.
Konieczny, Jochen
Rosenberger, Gerhard
and
Wolny, Julia
2000.
Tame Almost Primitive Elements.
Results in Mathematics,
Vol. 38,
Issue. 1-2,
p.
116.
Mikhalev, A. A.
2000.
Primitive elements and automorphisms of free algebras of schreier varieties.
Journal of Mathematical Sciences,
Vol. 102,
Issue. 6,
p.
4627.
Mikhalev, Alexander A.
and
Yu, Jie-Tai
2000.
Primitive, Almost Primitive, Test, and Δ-Primitive Elements of Free Algebras with the Nielsen–Schreier Property.
Journal of Algebra,
Vol. 228,
Issue. 2,
p.
603.
Artamonov, Vyacheslav
2003.
Polynomial Identities And Combinatorial Methods.
Klimakov, A. V.
and
Mikhalev, A. A.
2012.
Almost primitive elements of free nonassociative algebras of small ranks.
Journal of Mathematical Sciences,
Vol. 185,
Issue. 3,
p.
430.
Artamonov, V. A.
Klimakov, A. V.
Mikhalev, A. A.
and
Mikhalev, A. V.
2019.
Primitive and Almost Primitive Elements of Schreier Varieties.
Journal of Mathematical Sciences,
Vol. 237,
Issue. 2,
p.
157.


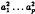 , or that
, or that 