Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lee, Sang Bum
2003.
n-Prüfer domains.
Bulletin of the Australian Mathematical Society,
Vol. 68,
Issue. 3,
p.
423.
Lee, Sang Bum
2003.
h-Divisible Modules.
Communications in Algebra,
Vol. 31,
Issue. 1,
p.
513.
Lee, Sang Bum
2006.
Weak-Injective Modules.
Communications in Algebra,
Vol. 34,
Issue. 1,
p.
361.
Bazzoni, Silvana
and
Herbera, Dolors
2009.
Cotorsion pairs generated by modules of bounded projective dimension.
Israel Journal of Mathematics,
Vol. 174,
Issue. 1,
p.
119.
Fuchs, László
and
Lee, Sang Bum
2009.
The Functor Hom and Cotorsion Theories.
Communications in Algebra,
Vol. 37,
Issue. 3,
p.
923.
Nikmehr, Mohammad Javad
and
Nikandish, Reza
2010.
HW-DIVISIBLE MODULES.
Asian-European Journal of Mathematics,
Vol. 03,
Issue. 03,
p.
475.


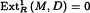 for all divisible
for all divisible 