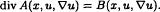Research Article
Twisted Alexander polynomial for the Braid group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
A note on Kummer theory of division points over singular Drinfeld modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 15-20
-
- Article
-
- You have access
- Export citation
Semi-Baer modules over domains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-26
-
- Article
-
- You have access
- Export citation
A permutability problem in infinite groups and Ramsey's theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 27-31
-
- Article
-
- You have access
- Export citation
On strict inclusions of weighted dirichlet spaces of monogenic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 33-50
-
- Article
-
- You have access
- Export citation
A 3-space problem related to the fixed point property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 51-61
-
- Article
-
- You have access
- Export citation
On admissible distributions attached to convolutions of Hilbert modular forms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 63-70
-
- Article
-
- You have access
- Export citation
Self-splitting Abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-79
-
- Article
-
- You have access
- Export citation
Blocks of homogeneous effect algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 81-98
-
- Article
-
- You have access
- Export citation
An exponential diophantine equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 99-105
-
- Article
-
- You have access
- Export citation
Radical extensions and crossed homomorphisms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 107-119
-
- Article
-
- You have access
- Export citation
A theorem on power series with applications to classical groups over finite fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 121-129
-
- Article
-
- You have access
- Export citation
On joint spectra of non-commuting hyponormal operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 131-136
-
- Article
-
- You have access
- Export citation
The space of p-summable sequences and its natural n-norm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-147
-
- Article
-
- You have access
- Export citation
Unique continuation for non-negative solutions of quasilinear elliptic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-156
-
- Article
-
- You have access
- Export citation
Inverse semigroup homomorphisms via partial group actions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 157-168
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Some aspects of saddlepoint approximations for non-parametric statistics
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-170
-
- Article
-
- You have access
- Export citation
On the derived length of finite, graded Lie rings with prime-power order, and groups with prime-power order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 171-172
-
- Article
-
- You have access
- Export citation
On monoids related to braid groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 173-176
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 64 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

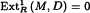 for all divisible
for all divisible