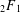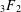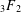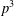Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Ji-Cai
2020.
On two congruences involving Franel numbers.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 4,
Guo, Victor J. W.
2022.
Some q-analogues of supercongruences for truncated $$_3F_2$$ hypergeometric series.
The Ramanujan Journal,
Vol. 59,
Issue. 1,
p.
131.
Pan, Hao
Tauraso, Roberto
and
Wang, Chen
2022.
A local-global theorem for p-adic supercongruences.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 790,
p.
53.
Sun, Zhi-Hong
2023.
Supercongruences involving products of three binomial coefficients.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 3,
Mao, Guo-Shuai
and
Liu, Yan
2024.
On two congruence conjectures of Z.-W. Sun involving Franel numbers.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 154,
Issue. 3,
p.
887.