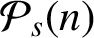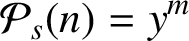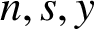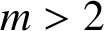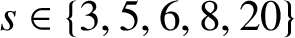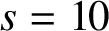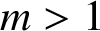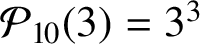A UNIQUE PERFECT POWER DECAGONAL NUMBER

Abstract

Let $\mathcal {P}_s(n)$ denote the nth s-gonal number. We consider the equation

$$ \begin{align*}\mathcal{P}_s(n) = y^m \end{align*} $$

for integers $n,s,y$ and m. All solutions to this equation are known for $m>2$ and $s \in \{3,5,6,8,20 \}$ . We consider the case $s=10$ , that of decagonal numbers. Using a descent argument and the modular method, we prove that the only decagonal number greater than 1 expressible as a perfect mth power with $m>1$ is $\mathcal {P}_{10}(3) = 3^3$ .

1. Introduction

The nth s-gonal number, with $s \geq 3$ , which we denote by $\mathcal {P}_s(n)$ , is given by the formula

$$ \begin{align*} \mathcal{P}_s(n) = \frac{(s-2)n^2-(s-4)n}{2}. \end{align*} $$

Polygonal numbers have been studied since antiquity [6, pages 1–39] and relations between different polygonal numbers and perfect powers have received much attention (see, for example, [7] and the references cited therein). Kim et al. [7, Theorem 1.2] found all solutions to the equation $\mathcal {P}_s(n) = y^m$ when $m>2$ and $s \in \{3,5,6,8,20 \}$ for integers n and y. We extend this result (for $m>1$ ) to the case $s=10$ , that of decagonal numbers.

Theorem 1.1. All solutions to the equation

(1.1) $$ \begin{align} \mathcal{P}_{10}(n) = y^m,\quad n,y,m \in \mathbb{Z},\quad m> 1 \end{align} $$

satisfy $n=y=0, n=|y|=1$ or $n=y=m=3$ .

In particular, the only decagonal number greater than 1 expressible as a perfect mth power with $m>1$ is $\mathcal {P}_{10}(3) = 3^3$ .

We will prove Theorem 1.1 by carrying out a descent argument to obtain various ternary Diophantine equations, to which one may associate Frey elliptic curves. The difficulty in solving the equation $\mathcal {P}_{s}(n) = y^m$ for a fixed value of s is due to the existence of the trivial solution $n=y=1$ (for any value of m). We note that adapting our method of proof also works for the cases $s \in \{3,5,6,8,20 \}$ mentioned above, but will not extend to any other values of s (see Remark 3.1).

2. Descent and small values of m

We note that it will be enough to prove Theorem 1.1 in the case $m=p$ , prime. We write (1.1) as

(2.1) $$ \begin{align} n(4n-3) = y^p, \quad n,y \in \mathbb{Z},\quad p \text{ prime}\end{align} $$

and suppose that $n,y \in \mathbb {Z}$ satisfy this equation with $n \ne 0$ .

Case 1: $3 \nmid n$

If $3 \nmid n$ , then n and $4n-3$ are coprime, so there exist coprime integers a and b such that

$$ \begin{align*} n = a^p \quad \text{ and } \quad 4n-3 = b^p. \end{align*} $$

It follows that

(2.2) $$ \begin{align} 4a^p-b^p = 3. \end{align} $$

If $p=2$ , we see that $(2a-b)(2a+b)=3$ , so that $a = b = \pm 1$ and so $n=|y|=1$ . If $p=3$ or $p=5$ , then using the Thue equation solver in Magma [5], we also find that $a=b=1$ .

Case 2: $3 \parallel n$

Suppose that $3 \parallel n$ (that is, $\mathrm {ord}_3(n)=1$ ). Then, after dividing (2.1) by $3^{\mathrm {ord}_3(y)p}$ , we see that there exist coprime integers t and u with $3 \nmid t$ such that

$$ \begin{align*}n = 3t^p \quad \text{ and } \quad 4n-3 = 3^{p-1}u^p. \end{align*} $$

Then

(2.3) $$ \begin{align} 4t^p-3^{p-2}u^p = 1. \end{align} $$

If $p=2$ , we have $(2t-u)(2t+u)=1$ , which has no solutions. If $p=3$ , then we have $4t^3-3u^3=1$ and, using the Thue equation solver in Magma [5], we verify that $u=t=1$ is the only solution to this equation. This gives $n=y=3$ . If $p=5$ , Magma’s Thue equation solver shows that there are no solutions.

Case 3: $3^2 \mid n$

If $3^2 \mid n$ , then $3 \parallel 4n-3$ and, arguing as in Case 2, there exist coprime integers v and w with $3 \nmid w$ such that

$$ \begin{align*}n = 3^{p-1}v^p \quad \text{ and } \quad 4n-3 = 3w^p. \end{align*} $$

So,

(2.4) $$ \begin{align} 4 \cdot 3^{p-2}v^p- w^p = 1. \end{align} $$

If $p=2$ , then as in Case 2 we obtain no solutions. If $p=3$ or $p=5$ , then we use Magma’s Thue equation solver to verify that there are no solutions with $v \ne 0$ .

3. Frey curves and the modular method

To prove Theorem 1.1, we will associate Frey curves to equations (2.2), (2.3) and (2.4) and apply Ribet’s level-lowering theorem [8, Theorem 1.1] to obtain a contradiction. We describe this process as level-lowering the Frey curve. We have considered the cases $p=2,3$ and $5$ in Section 2 and so we will assume that $m=p$ is prime with $p \geq 7$ .

We note that at this point we could directly apply [3, Theorem 1.2] to conclude that the only solutions to (3.1) are $a=b=1$ , giving $n=1$ , and apply [2, Theorem 1.2] to show that (3.2) and (3.3) have no solutions. The computations for (3.1) are not explicitly carried out in [3], so for the convenience of the reader and to highlight why the case $s=10$ is somewhat special, we provide some details of the arguments.

Case 1: $3 \nmid n$

We write (2.2) as

(3.1) $$ \begin{align} -b^p +4a^p = 3 \cdot 1^2, \end{align} $$

which we view as a generalised Fermat equation of signature $(p,p,2)$ . We note that the three terms are integral and coprime.

We suppose that $ab \ne \pm 1$ . Following the recipes of [3, pages 26–31], we associate Frey curves to (3.1). We first note that b is odd, since $b^p = 4n-3$ . If $a \equiv 1 \pmod {4}$ , we set

$$ \begin{align*}E_1: Y^2 = X^3 -3X^2+3a^pX. \end{align*} $$

If $a \equiv 3 \pmod {4}$ , we set

$$ \begin{align*}E_2: Y^2 = X^3 + 3X^2+3a^pX. \end{align*} $$

If a is even, we set

$$ \begin{align*}E_3: Y^2+XY = X^3 - X^2 + \frac{3a^p}{16} X. \end{align*} $$

We level-lower each Frey curve and find that for $i=1,2,3,$ we have $E_i \sim _p f_i$ for $f_i$ a newform at level $N_{p_i}$ , where $N_{p_1} = 36, N_{p_2} = 72$ and $N_{p_3} = 18$ . The notation $E \sim _p f$ means that the mod-p Galois representation of E arises from f. There are no newforms at level $18$ and so we focus on the curves $E_1$ and $E_2$ . There is a unique newform, $f_1$ , at level $36$ , and a unique newform, $f_2$ , at level $72$ .

The newform $f_1$ has complex multiplication by the imaginary quadratic field $\mathbb {Q}(\!\sqrt {-3})$ . This allows us to apply [3, Proposition 4.6]. Since $2 \nmid ab$ and $3 \nmid ab$ , we conclude that $p=7$ or $13$ and that all elliptic curves of conductor $2p$ have positive rank over $\mathbb {Q}(\!\sqrt {-3})$ . However, it is straightforward to check that this is not the case for $p=7$ and $13$ . We conclude that $E_1 \not \sim _p f_1$ .

Let $F_2$ denote the elliptic curve with Cremona label 72a2 whose isogeny class corresponds to $f_2$ . This elliptic curve has full two-torsion over the rationals and has j-invariant $2^{4} \cdot 3^{-2} \cdot 13^{3}$ . We apply [3, Proposition 4.4], which uses an image of inertia argument, to obtain a contradiction in this case too.

Remark 3.1. The trivial solution $a=b=1$ (or $n=y=1$ ) corresponds to the case $i=1$ above. The only reason we are able to discard the isomorphism $E_1 \sim _p f_1$ is because the newform $f_1$ has complex multiplication. The modular method would fail to eliminate the newform $f_1$ otherwise. For each value of s, we can associate to (1.1) generalised Fermat equations of signature $(p,p,2)$ , $(p,p,3)$ and $(p,p,p)$ . We found we could only obtain newforms with complex multiplication (when considering the case corresponding to the trivial solution) when $s = 3, 6, 8, 10$ or $20$ . A similar strategy of proof also works for $s=5$ using the work of Bennett [1, page 3] on equations of the form $(a+1)x^n-ay^n = 1$ to deal with the trivial solution.

Case 2: $3 \parallel n$

We rewrite (2.3) as

(3.2) $$ \begin{align} 4t^p-3^{p-2}u^p = 1 \cdot 1^3, \end{align} $$

which we view as a generalised Fermat equation of signature $(p,p,3)$ . The three terms are integral and coprime. We suppose that $tu \ne \pm 1$ . Using the recipes of [4, pages 1401–1406], we associate to (3.2) the Frey curve

$$ \begin{align*}E_4: Y^2 + 3XY - 3^{p-2}u^p \, Y = X^3. \end{align*} $$

We level-lower $E_4$ and find that $E_4 \sim _p f$ , where f is a newform at level $6$ , an immediate contradiction, as there are no newforms at level $6$ .

Case 3: $3^2 \mid n$

We rewrite (2.4) as

(3.3) $$ \begin{align} -w^p + 4 \cdot 3^{p-2}v^p = 1 \cdot 1^3, \end{align} $$

which we view as a generalised Fermat equation of signature $(p,p,3)$ . The three terms are integral and coprime. We suppose that $vw \ne \pm 1$ . The Frey curve we attach to (3.3) is

$$ \begin{align*} E_5: Y^2 + 3XY + 4 \cdot 3^{p-2} v^p \, Y = X^3. \end{align*} $$

We level-lower and find that $E_5 \sim _p f$ , where f is a newform at level $6$ , a contradiction as in Case 2.

This completes the proof of Theorem 1.1.