Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T05:40:34.749Z Has data issue: false hasContentIssue false
  • English
  • Français

Varieties of topological groups

Published online by Cambridge University Press:  17 April 2009

Sidney A. Morris
Sidney A. Morris
Affiliation:
University of Queensland, and The Flinders University of South Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

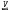We introduce the concept of a variety of topological groups and of a free topological group F(X, 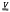) of 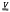on a topological space X as generalizations of the analogous concepts in the theory of varieties of groups. Necessary and sufficient conditions for F(X, 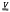) to exist are given and uniqueness is proved. We say the topological group FM,(X) is moderately free on X if its topology is maximal and it is algebraically free with X as a free basis. We show that FM(X) is a free topological group of the variety it generates and that if FM(X) is in 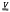then it is topologically isomorphic to a quotient group of F(X, 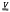). It is also shown how well known results on free (free abelian) topological groups can be deduced. In the algebraic theory there are various equivalents of a free group of a variety. We examine the relationships between the topological analogues of these. In the appendix a result similar to the Stone-Čech compactification is proved.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 1 , Issue 2 , August 1969 , pp. 145 - 160
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Graev, M.I., “Free topological groups”, Izvestiya Akad. Nauk SSSR. Ser Mat. 12 (1948), 279–321, (Russian). English transl., Amer. Math. Soc. Translation no. 35, 61 pp. (1951). Reprint, Amer. Math. Soc. Transl. (1) 8 (1962), 305–36.Google Scholar
[2]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis, Vol. I, (Academic Press, New York, 1963).Google Scholar
[3]Kakutani, Shizuo, “Free topological groups and infinite direct product topological groups”, Proc. Imp. Acad. Tokyo 20 (1944), 595–598.Google Scholar
[4]Kelley, J.L., General topology, (Van Nostrand, New York, 1955).Google Scholar
[5]Markov, A.A., “On free topological groups”, C.R. (Doklady) Acad. Sci. URSS, (N.S.) 31 (1941); 299–301. Bull. Acad. Sci. URSS. Sér. Math. [Izvestiya Akad. Nauk SSSR] 9 (1945), 3–64. (Russian. English summary). English transl., Amer. Math. Soc. Translation no. 30 (1950), 11–88; reprint Amer. Math. Soc. Transl. (1) 8 (1962), 195–273.Google Scholar
[6]Neumann, Hanna, Varieties of Groups, Ergebnisse der Mathematik, und ihrer Grenzgebiete, Band 37,(Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[7]Nielsen, R. and Sloyer, C., “On embedding in quasi-cubes”, Amer. Math. Monthly 75 (1968), 514–515.CrossRefGoogle Scholar