Research Article
Varieties of topological groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-160
-
- Article
-
- You have access
- Export citation
Comments on bases in dependence structures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-167
-
- Article
-
- You have access
- Export citation
A generalized Banach-Mazur theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-173
-
- Article
-
- You have access
- Export citation
The connectivity of total graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-181
-
- Article
-
- You have access
- Export citation
Analytic iterations on Riemann surfaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 183-194
-
- Article
-
- You have access
- Export citation
On regular semigroups whose idempotents form a subsemigroup
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 195-208
-
- Article
-
- You have access
- Export citation
Interior preserving maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 209-212
-
- Article
-
- You have access
- Export citation
Zero-free fortifying homomorphisms and semigroups of relations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-230
-
- Article
-
- You have access
- Export citation
On the lattice of congruences on a regular semigroup
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-235
-
- Article
-
- You have access
- Export citation
On the equivalence of a countable disjoint class of sets of positive measure and a weaker condition than total σ–finiteness of measures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 237-243
-
- Article
-
- You have access
- Export citation
On the group ring of a finite abelian group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-261
-
- Article
-
- You have access
- Export citation
Anti-uniform semilattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-268
-
- Article
-
- You have access
- Export citation
On the equivalence of invariant integrals and minimal ideals in semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 269-278
-
- Article
-
- You have access
- Export citation
The completion by cuts of an orthocomplemented modular lattice
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-280
-
- Article
-
- You have access
- Export citation
On Lie algebra obstructions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 281-288
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 1 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 1 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

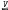 of topological groups and of a free topological group F(X,
of topological groups and of a free topological group F(X, 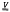 ) of
) of 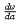 =
= 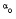 , the mapping
, the mapping 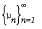 on
on 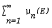 for all
for all 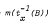 for every Borel
for every Borel