We study the inverse boundary value problem for fractional diffusion in a multilayer composite medium. Given data in the right boundary of the second layer, the problem is to recover the temperature distribution in the first layer, which is inaccessible for measurement. The problem is ill-posed and we propose a Fourier spectral approach to achieve Hölder approximations. The convergence analysis is performed in both the 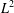 $L^{2}$- and
$L^{2}$- and 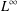 $L^{\infty }$-settings.
$L^{\infty }$-settings.