It is known that in a B*-algebra every self-adjoint element is hermitian. We give an elementary proof that this condition characterizes B*-algetras among Banach*-algebras.

It is shown that a von Neumann regular ring R is left seif-injective if and only if every finitely generated torsion-free left R-module is projective. It is further shown that a countable self-injective strongly regular ring is Artin semi-simple.

The Krull Galois theory for infinite separable normal extensions is generalized in this note to non-algebraic extensions. For any extension field E of a field K it is shown that the Galois group G can be given a translation invariant topology such that the closed subgroups are precisely the subgroups that figure in a Galois correspondence. For extension fields E/K such that E/K is of finite transcendence degree and such that E is Galois over each intermediate field the topology turns out to be compact and we have a Galois correspondence in the Krull fashion. For infinite transcendence degree extensions the Galois correspondence remains but compactness is lost. The topology coincides with the Krull topology in the case of algebraic extensions. Further properties of the topology are also studied.

It is veil-known that every ring automorphism of the ring of all linear transformations of a real vector space into itself is inner. We shall show that, if this ring is regarded as a semigroup with respect to composition and the dimension of the vector space is not less than 2, every semigroup automorphism is inner.

Let p be a prime and the variety of elementary abelian by elementary abelian p-groups. A result of Brisley and Macdonald is generalized as follows. If H is a finite group in and G is a soluble group of p–power exponent such that no section of G is isomorphic to H, then G is nilpotent and its class is bounded by a function of three variables: H, the exponent of G, and the soluble length of G. It is a corollary that if the variety generated by a soluble group G of finite exponent contains , then each finite group in is isomorphic to some section of G.

Some properties of projective planes having a certain type of collineation group are proved, and a class of these planes which properly contains the class of all Hall planes of odd order is explicitly constructed.

Let H(C) be the group of homeomorphisms of the cantor set, C onto itself. Let p: C → M be a (continuous) map of C onto a compact metric space M, and let G(p, M) be {h ∈ H(C) | ∀x ∈ C, p(x) = ph(x)}. G(p, M) is a group. The map p: C → M is standard, if for each (x, y) ∈ C × C such that p(x) = p(y), there is a sequence 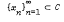and a sequence such that xn → x and hn(xn) → y. Standard maps and their associated groups characterize compact metric spaces in the sense that: Two such spaces, M and N, are homeomorphic if and only if, given p standard from C onto M, there is a standard q from C onto N for which G(p, M) = h−1G(q, N)h, for some h ∈ H(C). That is, two compact metric spaces are homeomorphic if and only if they determine, via standard maps, the same classes of conjugate subgroups of H(C).

The present note exhibits two natural structure theorems relating algebraic and topological properties: First, if M = H ∪ K (H, K ≠ π) , compact metric, and p : C → M are given, then G(p, M) is isomorphic to a subdirect product of G(p, M)/S(p, H\K) and G(p, M)/S(p, K\H) where, generally, S(p, N) is the normal subgroup of homeomorphisms supported on p−1M . Second, given M and N compact metric and p : M → N continuous and onto, let M ≠ M − CID*α ≠ 0 , where {Dα}α ∈ A is the collection of non-degenerate preimages of points in N Then there is a standard p : C → M such that fp : C → N is standard and there is a homomorphism

.

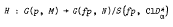We give a simplified proof of a general theorem of Chunikhin on existence of subgroups of a finite group. The proof avoids the technical device of “indexials” which Chunikhin set up for this purpose.

Let be a Cross variety and let n be the least integer such that (n) is locally finite; then n ≤ 2d + 3 where d is an upper bound for the number of generators of certain critical groups in .

The equation of motion of charged incoherent matter, and hence of a test charge, in general relativity can be written as the geodesic equation of an affine connection. Here, the connection is chosen to satisfy a condition which has the form of one of the basic geometrical principles of Einstein's unified field theory. The symmetric part of the fundamental tensor of the geometry is chosen to be the metric tensor of general relativity; equations to be satisfied by the skew part, involving the electromagnetic field, are obtained. An alternative condition on the affinity is also considered.

Maximal sum-free sets in elementary abelian 3-groups and groups G = Z3 ⊕ Z3 ⊕ Zp where p is a prime congruent to 1 modulo 3 are completely characterized.

We show

(i) that the Rayleigh-Ritz method is a practical procedure for obtaining approximations to the velocity potential for compressible flows, and

(ii) how to calculate an estimate of the error in such approximations.

A subset S of an additive group G is called a maximal sum-free set in G if (S+S) ∩ S = ø and |S| ≥ |T| for every sum-free set T in G. In this paper, the maximal sum-free sets in cyclic p–groups are characterized to within automorphism.

This paper deals with the motion of a point test charge in an external electromagnetic field with the effect of electromagnetic radiation reaction included. The equation of motion applicable in a general Riemannian space-time is written as the geodesic equation of an affine connection. The connection is the sum of the Christoffel connection and a tensor which depends on, among other things, the external electromagnetic field, the charge and mass of the particle and the Ricci tensor. The affinity is not unique; a choice is made so that the covariant derivative of the metric tensor with respect to the connection vanishes. The special cases of conformally flat spaces and the space of general relativity are discussed.

We construct a family of groups with precisely NO full orders.

This paper examines a class of common numerical methods for computing eigenvectors of a compact linear operator. A necessary and sufficient condition is established for every element of an arbitrary given eigenspace to be the limit of a sequence of the approximate eigenvectors obtained by any given method in this class.

An upper bound is given of the dimension of certain spaces of cusp harmonic forms of arithmetic subgroups Γ of semisimple algebraic groups G in terms of the multiplicities of corresponding irreducible unitary representations of the group GR of real rational points of G in the space 0L2(GR/Γ) of cusp forms.

The purpose of this paper is to show that there exists an infinite family of non-invertible prime 2-component links in S3. It is then noted that the existence of such a family implies the existence of a family of non-invertible wild arcs in S3, which are tame modulo an endpoint.