Some new integral conditions characterising the embedding ∧p(v) ↪ Γq(w), 0 < p, q ≤ ∞ are presented, including proofs also for the cases (i) p = ∞, 0 < q < ∞, (ii) q = ∞, I < p < ∞ and (iii) p = q = ∞. Only one condition is necessary for each case which means that our conditions are different from and simpler than other corresponding conditions in the literature. We even prove our results in a more general frame namely when the space Γq(w) is replaced by the more general space . In our proof we use a technique of discretisation and anti-discretisation developed by A. Gogatishvili and L. Pick, where they considered the opposite embedding.

We study some convergence of two kinds of implicit iteration processes for approximating common fixed points of a pseudo-contractive semigroup in uniformly convex Banach spaces with uniformly Gateaux differential norms. As special cases, we get some convergence of the implicit iteration processes for approximating common fixed points of a nonexpansive semigroup in uniformly smooth Banach spaces and give a positive answer to an open problem proposed by Xu in Bull. Austral. Math. Soc. (2005). The results presented in this paper generalise some corresponding results from Osilike in Panamer. Math. J. (2004), Suzuki in Proc. Amer. Math. Soc. (2002) and Xu in Bull. Austral. Math. Soc. (2005).

For a supernilpotent radical α and a special class σ of rings we call a ring R (α, σ)-essential if R is α-semisimple and for each ideal P of R with R/P ε σ, P ∩ I ≠ 0 whenever I is a nonzero two-sided ideal of R. (α, σ)-essential rings form a generalisation of prime essential rings introduced by L. H. Rowen in his study of semiprime rings and their subdirect decompositions and they have been a subject of investigations of many prominent authors since. We show that many important results concerning prime essential rings are also valid for (α, σ)-essential rings and demonstrate how (α, σ)-essential rings can be used to determine whether a supernilpotent radical is special. We construct infinitely many supernilpotent nonspecial radicals whose semisimple class of prime rings is zero and show that such radicals form a sublattice of the lattice of all supernilpotent radicals. This generalises Yu.M. Ryabukhin's example.

We study a construction algorithm for certain polynomial lattice rules modulo arbitrary polynomials. The underlying polynomial lattices are special types of digital nets as introduced by Niederreiter. Dick, Kuo, Pillichshammer and Sloan recently introduced construction algorithms for polynomial lattice rules modulo irreducible polynomials which yield a small worst-case error for integration of functions in certain weighted Hilbert spaces. Here, we generalize these results to the case where the polynomial lattice rules are constructed modulo arbitrary polynomials.

In this paper we obtain criteria of stability for ηEinstein k-contact manifolds, for Sasakian manifolds of constant ϕ-sectional curvature and for 3-dimensional Sasakian manifolds. Moreover, we show that a stable compact Einstein contact metric manifold M is Sasakian if and only if the Reeb vector field ξ minimises the energy functional. In particular, the Reeb vector field of a Sasakian manifold M of constant ϕ-holomorphic sectional curvature +1 minimises the energy functional if and only if M is not simply connected.

We are concerned with existence and stability of solutions for system of equations with generalised p(x) and m(x)—Laplace operators and where the nonlinearity satisfies some local growth conditions. We provide a variational approach that is based on investigation of the primal and the dual action functionals. As a consequence we consider the dependence of the the system on functional parameters.

Based on Haldane's spherical geometrical formalism of the two-dimensional quantum Hall fluids, the relation between the noncommutative geometry of S2 and the two-dimensional quantum Hall fluids is exhibited. A finite matrix model on the two-sphere is explicitly constucted as an effective description of the fractional quantum Hall fluids of finite extent, and the complete sets of physical quantum states of this matrix model are determined. We also describe how the low-lying excitations in the model are constructed in terms of the quasi-particle and quasi-hole excitations. It is shown that there exists a Haldane hierarchical structure in the two-dimensional quantum Hall fluid states of the matrix model. These hierarchical fluid states are generated by the parent fluid state by condensing the quasi-particle and quasi-hole excitations level by level.

Let p be a prime number ≥ 5, and n a positive integer > 1. This note is concerned with the diophantine equation x4 − y4 = nzp. We prove that, under certain conditions on n, this equation has no non-trivial solution in Z if p ≥ C(n), where C(n) is an effective constant.

In this paper, we prove an analogue of Beurling's theorem on the Heisenberg group. Then we derive some other versions of the uncertainty principle.

We show that a suitable adaptation of the so-called method of trajectories can be used to construct an exponential attractor for a very general class of nonlinear reaction-diffusion systems with a bounded delay.

In particular, we assume that the dependence on the past history is controlled via convolution with a possibly singular measure. Assuming a priori that the solutions are bounded, a simple proof of the existence of an exponential attractor is given under very little regularity requirements.

In this paper we prove partial regularity for a weakly stable p-harmonic map from Ω into Sk when k > 2p – 1.

Nelsen [J. Algebra 298 (2006) 134–141] asked whether there is a natural class of McCoy rings which includes all reversible rings and all rings R such that R[X] is semi-commutative. In this paper, some new equivalent conditions of McCoy rings are given. One of them is used to answer this question in the affirmative. Finally, an example is given which is McCoy and semi-commutative, but it is not reversible and does not have the property that R[x] is semi-commutative.

Finite group theorists have been interested in counting groups of prime-power order, as a preliminary step to counting groups of any finite order and to assist in explicitly listing such groups. In 1960, G. Higman considered when the functions giving the number of groups of prime-power order pn, for fixed n and varying p, is of a particular form, called polynomial on residue classes (PORC). The suggestion that such counting functions are PORC is known as Higman's PORC conjecture. In his 1960 paper [4] he proved that a certain class of groups of prime-power order, now called exponent-p class two groups, have counting functions that are PORC, but did not furnish explicit PORC functions.

We show that linear operators from a Banach space into itself which satisfy some relaxed strong accretivity conditions are invertible. Moreover, we characterise a particular class of such operators in the Hilbert space case. By doing so we manage to answer a problem posed by B. Ricceri, concerning a linear second order partial differential operator.

Let G be a graph of order n, and let a, b, k be nonnegative integers with 1 ≤ a < b. An [a, b]-factor of graph G is defined as a spanning subgraph F of G such that a ≤ dF(x) ≤ b for each x ϵ V (F). Then a graph G is called an (a, b, k)-critical graph if after deleting any k vertices of G the remaining graph of G has an [a, b]-factor. In this paper, it is proved that G is an (a, b, k)-critical graph if the binding number 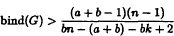and

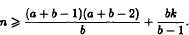
Furthermore, it is showed that the result in this paper is best possible in some sense.

In a recent paper Miranda Jr., Pallara, Paronetto and Preunkert have shown that the classical De Giorgi's heat kernel characterisation of functions of bounded variation on Euclidean space extends to Riemannian manifolds with Ricci curvature bounded from below and which satisfy a uniform lower bound estimate on the volume of geodesic balls of fixed radius. We give a shorter proof of the same result assuming only the lower bound on the Ricci curvature.

This paper looks at simple rings which have right ideals satisfying various types of injectivity conditions. We characterise when a simple regular ring is right self-injective and show that if R is a simple ring in which every right ideal is the direct sum of quasi-continuous right ideals then R is either Artinian or a non-selfinjective right Goldie ring in which every right ideal is a direct sum of uniform right ideals.