Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T01:12:18.868Z Has data issue: false hasContentIssue false
  • English
  • Français

Actions That Fiber and Vector Semigroups

Published online by Cambridge University Press:  20 November 2018

T. H. McH. Hanson
T. H. McH. Hanson*
Affiliation:
The University of Georgia, Athens, Georgia; The University of Florida, Gainesville, Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

From [2], we can derive a criterion for determining when an action of a Lie group on a locally compact space leads to a fiber bundle. Here, we present an equivalent criterion which can be stated purely in the language of actions of groups on spaces. This is Theorem I. Using this result, we are able to give a version of a result of Home [1] for dimensions greater than one. This is done in Theorem IV and Corollary IVA. In Theorem II, we show that if a vector semigroup 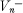acts on a space X, then whenever the map t ↦ tx is 1 — 1 from 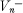onto 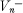x, it is in fact a homeomorphism. Also, 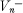is a closed subset of X. This is also a version of a result in [1].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 1 , February 1972 , pp. 29 - 37
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Home, J. G., Flows that fiber and some semigroup questions, Notices Amer. Math. Soc. 13 (1966), 821.Google Scholar
2. Paul S., Mostert, Sections in principal fiber spaces, Duke Math. J. 23 (1956), 57–71.Google Scholar
3. Steenrod, N. E., The topology of fiber bundles (Princeton University Press, Princeton, N.J., 1951).Google Scholar