Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T03:03:35.804Z Has data issue: false hasContentIssue false
  • English
  • Français

Baer Subplanes in Finite Projective and Affine Planes

Published online by Cambridge University Press:  20 November 2018

Judita Cofman
Judita Cofman*
Affiliation:
Mathematisches Institut, Universität Tübingen
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let π be a projective or an affine plane ; a configuration C of π is a subset of points and a subset of lines in π such that a point P of C is incident with a line I of C if and only if P is incident with I in π. A configuration of a projective plane π which is a projective plane itself is called a projective subplane of π, and a configuration of an affine plane π’ which is an affine plane with the improper line of π‘ is an affine subplane of π‘.

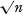Let π be a finite projective (respectively, an affine) plane of order n and π0 a projective (respectively, an affine) subplane of π of order n0 different from π; then n0 ≦ . If n0 = 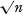, then π0 is called a Baer subplane of π. Thus, Baer subplanes are the “biggest” possible proper subplanes of finite planes.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 1 , February 1972 , pp. 90 - 97
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Baer, R., Projectivities of finite projective planes, Amer. J. Math. 69 (1947), 653–684.Google Scholar
2. Cofman, J., On Baer involutions of finite projective planes, Can. J. Math. 22 (1970), 878–880.Google Scholar
3. Dembowski, P., Finite geometries (Springer Verlag, Berlin-Heidelberg-New York, 1969).Google Scholar
4. Hall, M., The theory of groups (Macmillan, New York, 1959).Google Scholar
5. Lenz, H., Zur Begründung der analytischen Géométrie, S.-B. Math.-Nat. Kl. Bayer. Akad. Wiss. 1954, 17-22 (1955).Google Scholar