Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Parrott, David
1973.
A characterization of the Ree groups 2F4(q).
Journal of Algebra,
Vol. 27,
Issue. 2,
p.
341.
Parrott, David
1973.
On the Simple Group of J. Tits.
Canadian Mathematical Bulletin,
Vol. 16,
Issue. 1,
p.
87.
Stroth, G
1976.
A characterization of Fischer's sporadic simple group of the order 241 · 313 · 56 · 72 · 11 · 13 · 17 · 19 · 23 · 31 · 47.
Journal of Algebra,
Vol. 40,
Issue. 2,
p.
499.
Assa, Steven Brent
1976.
A characterization of 2F4(2)′ and the Rudvalis group.
Journal of Algebra,
Vol. 41,
Issue. 2,
p.
473.
Gorenstein, Daniel
1979.
The classification of finite simple groups I. Simple groups and local analysis.
Bulletin of the American Mathematical Society,
Vol. 1,
Issue. 1,
p.
43.
Wester, Michael
1980.
Endliche Gruppen, die eine Involution z besitzen, so daβ F∗(C(z)) das direkte Produkt einer extraspeziellen 2-Gruppe von kleiner Weite mit einer elementarabelschen 2-Gruppe ist, II.
Journal of Algebra,
Vol. 66,
Issue. 1,
p.
12.
Stroth, Gernot
1980.
A general characterization of the tits simple group.
Journal of Algebra,
Vol. 64,
Issue. 1,
p.
140.
Arad, Zvi
and
Ward, Michael B
1982.
New criteria for the solvability of finite groups.
Journal of Algebra,
Vol. 77,
Issue. 1,
p.
234.
Walker, Michael
1983.
On Central Root Automorphisms of Finite Generalized Octagons.
European Journal of Combinatorics,
Vol. 4,
Issue. 1,
p.
65.
Ferguson, Pamela A.
1985.
On π-homogeneity and π′-closure.
Journal of Algebra,
Vol. 96,
Issue. 1,
p.
230.
Makhnev, A. A.
1986.
Finite groups containing fine 2-local subgroups.
Siberian Mathematical Journal,
Vol. 26,
Issue. 5,
p.
707.
Michler, Gerhard O.
and
Wang, Lizhong
2008.
Another Existence and Uniqueness Proof of the Tits Group.
Algebra Colloquium,
Vol. 15,
Issue. 02,
p.
241.
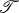 of index 2. In this paper we prove the following theorem:
of index 2. In this paper we prove the following theorem: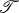 , the simple group of Tits, as defined in [6].
, the simple group of Tits, as defined in [6].