No CrossRef data available.
Article contents
A Class of Non-Central E-Functors
Published online by Cambridge University Press: 20 November 2018
Extract
We refer the reader to [1, Chapters 1 and 2] for the notions of E-functor and centrality. Let R1 ⊆ R be the integral group rings of the groups G1⊆ G. Butler and Horrocks [1, Chapter 26] have shown that on the category 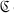 of left, unitary R-modules the Hochschild E-functor determined by R1 is central. There are no examples of non-central Hochschild E-functors, and our purpose is to establish the existence of a class of such E-functors.
of left, unitary R-modules the Hochschild E-functor determined by R1 is central. There are no examples of non-central Hochschild E-functors, and our purpose is to establish the existence of a class of such E-functors.
Take G to be finite, non-abelian and let 5 be the centre of R. Denote by φ the Hochschild E-functor determined by S. We obtain a necessary condition for the centrality of φ in terms of the group structure of G. Let G* denote the subgroup of G generated by the commutators of G together with the set ﹛gh(g): g £ G﹜, where h(g) is the class number of g in G.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972


