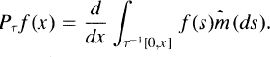Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Boyarsky, A
and
Góra, P
1990.
Compactness of eigenvectors for certain families of non-negative matrices.
Journal of Mathematical Analysis and Applications,
Vol. 150,
Issue. 2,
p.
425.
Góra, P.
and
Boyarsky, A.
1990.
Absolutely continuous invariant measures for the family of maps x → rxe-bxwith application to the Belousov-Zhabotinski reaction.
Dynamics and Stability of Systems,
Vol. 5,
Issue. 2,
p.
65.
Boyarsky, A.
Gora, P.
and
Lou, Y. S.
1994.
Constructive approximations to the invariant densities of higher-dimensional transformations.
Constructive Approximation,
Vol. 10,
Issue. 1,
p.
1.
Isabelle, S.H.
and
Wornell, G.W.
1995.
Statistical properties of one-dimensional chaotic signals.
Vol. 2,
Issue. ,
p.
1352.
Jabłoński, M.
Góra, P.
and
Boyarsky, A.
1995.
Invariant measures generated by sequences of approximating transformations.
Computers & Mathematics with Applications,
Vol. 30,
Issue. 7,
p.
75.
Góra, P.
and
Boyarsky, A.
1996.
An algorithm to control chaotic behavior in one-dimensional maps.
Computers & Mathematics with Applications,
Vol. 31,
Issue. 6,
p.
13.
Isabelle, S.H.
and
Wornell, G.W.
1997.
Statistical analysis and spectral estimation techniques for one-dimensional chaotic signals.
IEEE Transactions on Signal Processing,
Vol. 45,
Issue. 6,
p.
1495.
Rovatti, R.
and
Setti, G.
1997.
Statistical features and robustness of chaotic fuzzy maps.
Vol. 2,
Issue. ,
p.
793.
Blank, Michael
and
Keller, Gerhard
1997.
Stochastic stability versus localization in one-dimensional chaotic dynamical systems.
Nonlinearity,
Vol. 10,
Issue. 1,
p.
81.
Hunt, Fern Y
1998.
Unique ergodicity and the approximation of attractors and their invariant measures using Ulam's method.
Nonlinearity,
Vol. 11,
Issue. 2,
p.
307.
Góra, Pawel
and
Boyarsky, Abraham
1998.
A new approach to controlling chaotic systems.
Physica D: Nonlinear Phenomena,
Vol. 111,
Issue. 1-4,
p.
1.
Haydn, Nicolai
2004.
Convergence of the natural approximations of piecewise monotone interval maps.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 14,
Issue. 2,
p.
224.
�berg, Anders
2005.
Algorithms for approximation of invariant measures for IFS.
manuscripta mathematica,
Vol. 116,
Issue. 1,
p.
31.
Wing Shing Wong
and
Hui Cheng
2007.
Invariant distributions of linear systems under finite communication bandwidth feedback.
p.
2247.
Góra, Paweł
Li, Zhenyang
and
Boyarsky, Abraham
2012.
Harmonic average of slopes and the stability of absolutely continuous invariant measure.
Journal of Mathematical Analysis and Applications,
Vol. 396,
Issue. 1,
p.
1.
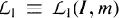 be the space of all integrable functions on I, where m denotes Lebesque measure on I. Let ∥ ∥1 be the ℒ-1-norm and let
be the space of all integrable functions on I, where m denotes Lebesque measure on I. Let ∥ ∥1 be the ℒ-1-norm and let 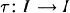 be a measurable, nonsingular transformation on I. Let
be a measurable, nonsingular transformation on I. Let 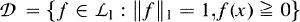 denote the space of densities. The probability measure μ is invariant under τ if for all measurable sets A,
denote the space of densities. The probability measure μ is invariant under τ if for all measurable sets A, 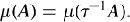 The measure μ is absolutely continuous if there exists an
The measure μ is absolutely continuous if there exists an 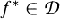 such that for any measurable set A
such that for any measurable set A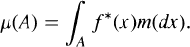 We refer to ƒ* as the invariant density of τ (with respect to m). It is well-known that ƒ * is a fixed point of the Frobenius-Perron operator
We refer to ƒ* as the invariant density of τ (with respect to m). It is well-known that ƒ * is a fixed point of the Frobenius-Perron operator 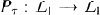 defined by
defined by