Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T15:16:30.726Z Has data issue: false hasContentIssue false
  • English
  • Français

Correction to: Upper Bounds for the Resonance Counting Function of Schrödinger Operators in Odd Dimensions

Published online by Cambridge University Press:  20 November 2018

Richard Froese
Richard Froese*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The proof of Lemma 3.4 in 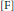$\left[ \text{F} \right]$ relies on the incorrect equality 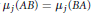${{\mu }_{j}}(AB)={{\mu }_{j}}(BA)$ for singular values (for a counterexample, see [S, p. 4]). Thus, Theorem 3.1 as stated has not been proven. However, with minor changes, we can obtain a bound for the counting function in terms of the growth of the Fourier transform of 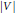$\left| V \right|$.

Keywords

47A1047A4081U05
Type
Correction
Information
Canadian Journal of Mathematics , Volume 53 , Issue 4 , 01 August 2001 , pp. 756 - 757
Copyright
Copyright © Canadian Mathematical Society 2001

References

[F] Froese, Richard, Upper bounds for the resonance counting function of Schrödinger operators in odd dimensions. Canad. J. Math. 50(1998), 538–546.Google Scholar
[S] Simon, Barry, Trace Ideals and their Applications. London Math. Soc. Lecture Note Ser. 35, Cambridge University Press, Cambridge, 1979.Google Scholar