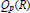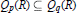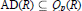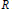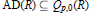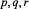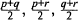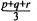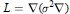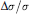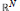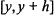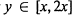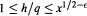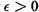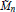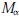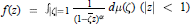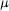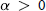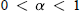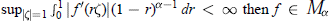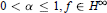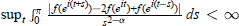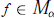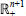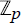Research Article
Qp Spaces on Riemann Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-464
-
- Article
-
- You have access
- Export citation
Six Primes and an Almost Prime in Four Linear Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-486
-
- Article
-
- You have access
- Export citation
On the Liouville Property for Divergence Form Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 487-496
-
- Article
-
- You have access
- Export citation
Morse Index of Approximating Periodic Solutions for the Billiard Problem. Application to Existence Results
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-524
-
- Article
-
- You have access
- Export citation
Nilpotent Orbit Varieties and the Atomic Decomposition of the Q-Kostka Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-537
-
- Article
-
- You have access
- Export citation
Upper Bounds for the Resonance Counting Function of Schrödinger Operators in Odd Dimensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 538-546
-
- Article
-
- You have access
- Export citation
Mittag-Leffler Theorems on Riemann Surfaces and Riemannian Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-562
-
- Article
-
- You have access
- Export citation
Primes in Short Segments of Arithmetic Progressions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 563-580
-
- Article
-
- You have access
- Export citation
The Homology of Singular Polygon Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 581-594
-
- Article
-
- You have access
- Export citation
Multipliers of Fractional Cauchy Transforms and Smoothness Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 595-604
-
- Article
-
- You have access
- Export citation
Hardy Spaces of Conjugate Systems of Temperatures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 605-619
-
- Article
-
- You have access
- Export citation
The Eichler Trace of ℤp Actions on Riemann Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 620-637
-
- Article
-
- You have access
- Export citation
Fractals in the Large
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 638-657
-
- Article
-
- You have access
- Export citation
Hankel Operators on Pseudoconvex Domains of Finite Type in ℂ2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-672
-
- Article
-
- You have access
- Export citation