Hostname: page-component-66644f4456-srn29 Total loading time: 0 Render date: 2025-02-13T07:46:56.174Z Has data issue: true hasContentIssue false
  • English
  • Français

Diophantine Approximation and Horocyclic Groups

Published online by Cambridge University Press:  20 November 2018

R. A. Rankin
R. A. Rankin*
Affiliation:
The University Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Let ω be an irrational number. It is well known that there exists a positive real number h such that the inequality

(1)

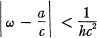
has infinitely many solutions in coprime integers a and c. A theorem of Hurwitz asserts that the set of all such numbers h is a closed set with supremum √5. Various proofs of these results are known, among them one by Ford (1), in which he makes use of properties of the modular group. This approach suggests the following generalization.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 9 , 1957 , pp. 277 - 290
Copyright
Copyright © Canadian Mathematical Society 1957

References

1. Ford, L. R., A geometrical proof of a theorem of Hurwitz, Proc. Edinburgh Math. Soc, 85 (1917), 59–65.Google Scholar
2. Ford, L. R., Automorphic functions (New York, 1929).Google Scholar
3. Petersson, H., Zur analytischen Théorie der Grenzkreisgruppen I, Math. Ann., 15 (1938), 23–67.Google Scholar
4. Rankin, R. A., On horocyclic groups, Proc. London Math. Soc. (3), 4 (1954), 219–234.Google Scholar
5. Scott, W. T., Approximation to real irrationals by certain classes of rational fractions, Bull. Amer. Math. Soc, 46 (1940), 124–29.Google Scholar
6. Tornheim, L., Approximation to irrationals by classes of rational numbers, Proc. Amer. Math. Soc, 6 (1955), 260–264.Google Scholar