Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-02T22:08:19.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant Polynomial Automorphisms Of Θ-Representations

Published online by Cambridge University Press:  20 November 2018

Alexandre Kurth
Alexandre Kurth*
Affiliation:
Department of Mathematics University of British Columbia Vancouver, BC V6T 1Z2
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that every equivariant polynomial automorphism of a 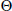$\Theta $- representation and of the reduction of an irreducible 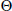$\Theta $-representation is a multiple of the identity.

Keywords

14L3014L27
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 2 , 01 April 1998 , pp. 378 - 400
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. A’Campo-Neuen, A., Morphisms of G-modules with finite fibers. C. R. Acad. Sci. Paris Sér. I 316(1992), 255–260.Google Scholar
2. Bröcker, T. and Dieck, T. tom, Representations of Compact Groups. Graduate Texts inMath. 98, Springer- Verlag, Berlin-New York, 1985.Google Scholar
3. Dadok, J. and Kac, V.G., Polar Representations. J. Algebra. 92(1985), 504–524.Google Scholar
4. Élashvili, A. G., Canonical Form and Stationary Subalgebras of Points of General Position for Simple Linear Lie Groups. Functional Anal. Appl. 6(1972), 44–53.Google Scholar
5. Élashvili, A. G., Stationary Subalgebras of Points of the Common State for Irreducible Linear Lie Groups. Functional Anal. Appl. 6(1972), 139–148.Google Scholar
6. Hartshorne, R., Algebraic Geometry. Graduate Texts in Math. 52, Springer-Verlag, Berlin-New York, 1977.Google Scholar
7. Kac, V.G., Automorphisms of Finite Order of Semisimple Lie Algebras. Functional Anal. Appl. 3(1969), 252–254.Google Scholar
8. Kac, V.G., Some Remarks on Nilpotent Orbits. J. Algebra 64(1980), 190–213.Google Scholar
9. Kraft, H., Geometrische Methoden in der Invariantentheorie.Aspekte derMathematik D1,Vieweg, 1985.Google Scholar
10. Kraft, H., Klassische Invariantentheorie: Eine Einführung. In: Algebraische Transformationsgruppen und Invariantentheorie, Algebraic Transformation Groups and Invariant Theory (Eds. Kraft, H., Slodowy, P. and Springer, T.A.). DMV Seminar Band 13, Birkhäuser, 1989. 41–62.Google Scholar
11. Kraft, H., Petrie, T. and Randall, J.D., Quotient Varieties. Adv. in Math. (2) 74(1989), 145–162.Google Scholar
12. Kurth, A., Equivariant Polynomial Automorphisms. Ph.D. Thesis, Basel, 1996.Google Scholar
13. Kurth, A., SL2-equivariant polynomial automorphisms of the binary forms. Ann. Inst. Fourier, Grenoble (2) 47(1997), 585–597.Google Scholar
14. Kurth, A., Nonlinear Equivariant Automorphisms. Manuscripta Math., 94(1997), 327–335.Google Scholar
15. Littelmann, P., Koreguläre und äquidimensionale Darstellungen. J. Algebra. 123(1989), 193–222.Google Scholar
16. Luna, D., Slices étales. Bull. Soc. Math. France,Mémoire 33(1973), 81–105.Google Scholar
17. Matsushima, Y., Espace homogéne de Stein des groupes de Lie complexes. Nagoya Math. J. 16(1960), 205–218.Google Scholar
18. Popov, A.M., Finite isotropy subgroups in general position of irreducible semisimple linear Lie groups. Trans. Moscow Math. Soc. 50(1988), 205–249.Google Scholar
19. Popov, V.L. and Vinberg, E.B., Invariant Theory. In: Algebraic Geometry IV (Eds. Parshin, A.N. and Shafarevich, I.R.),Encyclopaedia ofMathematical SciencesVol. 55. Springer-Verlag,Berlin-Heidelberg, 1994. 123–278.Google Scholar
20. Sato, M. and Kimura, T., A classification of irreducible prehomogeneous vector spaces and their relative invariants. Nagoya Math. J. 65(1977), 1–155.Google Scholar
21. Schwarz, G.W., Representations of Simple Lie Groups with a Free Module of Covariants. Invent. Math. 50(1978), 1–12.Google Scholar
22. Serre, J.P., Cohomologie Galoisienne. Lecture Notes in Math. 5, Springer-Verlag, Berlin-New York, 1964.Google Scholar
23. Springer, T.A., Invariant Theory. Lecture Notes in Math. 585, Springer-Verlag, Berlin-New York, 1977.Google Scholar
24. Vinberg, E.B., The Weyl group of a graded Lie algebra. Math. USSR-Izv. (3) 10(1976), 463–495.Google Scholar
25. Vinberg, E.B. and Élashvili, A. G., A classification of trivectors of a nine-dimensional space. Sel. Math. Sov. (1) 7(1978), 63–98.Google Scholar
26. Weyl, H., The Classical Groups, their Invariants and Representations. Second edition, Princeton University Press, Princeton, NJ, 1946.Google Scholar