1 Introduction
1.1
Let G be a simple algebraic group with
![]() ${\mathfrak g}={\mathrm {Lie\,}} G$
,
${\mathfrak g}={\mathrm {Lie\,}} G$
,
![]() ${\mathfrak g}={\mathfrak u}\oplus {\mathfrak t}\oplus {\mathfrak u}^-$
a fixed triangular decomposition, and
${\mathfrak g}={\mathfrak u}\oplus {\mathfrak t}\oplus {\mathfrak u}^-$
a fixed triangular decomposition, and
![]() ${\mathfrak b}={\mathfrak u}\oplus {\mathfrak t}$
the fixed Borel subalgebra. Then
${\mathfrak b}={\mathfrak u}\oplus {\mathfrak t}$
the fixed Borel subalgebra. Then
![]() $\Delta $
is the root system of
$\Delta $
is the root system of
![]() $({\mathfrak g},{\mathfrak t})$
,
$({\mathfrak g},{\mathfrak t})$
,
![]() $\Delta ^+$
is the set of positive roots corresponding to
$\Delta ^+$
is the set of positive roots corresponding to
![]() ${\mathfrak u}$
, and
${\mathfrak u}$
, and
![]() $\theta $
is the highest root in
$\theta $
is the highest root in
![]() $\Delta ^+$
. Write
$\Delta ^+$
. Write
![]() $U,T,B$
for the connected subgroups of G corresponding to
$U,T,B$
for the connected subgroups of G corresponding to
![]() ${\mathfrak u},{\mathfrak t},{\mathfrak b}$
.
${\mathfrak u},{\mathfrak t},{\mathfrak b}$
.
Let
![]() $P=L{\cdot }N$
be a parabolic subgroup of G, with the unipotent radical N and a Levi subgroup L. Then
$P=L{\cdot }N$
be a parabolic subgroup of G, with the unipotent radical N and a Levi subgroup L. Then
![]() ${\mathfrak n}={\mathrm {Lie\,}} N$
is the nilradical of
${\mathfrak n}={\mathrm {Lie\,}} N$
is the nilradical of
![]() ${\mathfrak p}={\mathrm {Lie\,}} P$
. The unipotent radicals of the parabolic subgroups provide an important class of non-reductive groups. For instance, N is a Grosshans subgroup of G [Reference Grosshans11, Theorem 16.4]. Various results on the coadjoint representation of
${\mathfrak p}={\mathrm {Lie\,}} P$
. The unipotent radicals of the parabolic subgroups provide an important class of non-reductive groups. For instance, N is a Grosshans subgroup of G [Reference Grosshans11, Theorem 16.4]. Various results on the coadjoint representation of
![]() ${\mathfrak n}$
can be found in [Reference Elashvili9, Reference Elashvili and Ooms10, Reference Ooms19, Reference Panyushev22]. Our main goal is to elaborate on invariant-theoretic properties of the coadjoint representation
${\mathfrak n}$
can be found in [Reference Elashvili9, Reference Elashvili and Ooms10, Reference Ooms19, Reference Panyushev22]. Our main goal is to elaborate on invariant-theoretic properties of the coadjoint representation
![]() $(N:{\mathfrak n}^{*})$
, but we also consider actions of some larger unipotent groups on
$(N:{\mathfrak n}^{*})$
, but we also consider actions of some larger unipotent groups on
![]() ${\mathfrak n}^{*}$
.
${\mathfrak n}^{*}$
.
Without loss of generality, we may assume that
![]() ${\mathfrak p}$
is standard, i.e.,
${\mathfrak p}$
is standard, i.e.,
![]() ${\mathfrak p}\supset {\mathfrak b}$
. Then
${\mathfrak p}\supset {\mathfrak b}$
. Then
![]() ${\mathfrak n}\subset {\mathfrak u}$
is a sum of root spaces and
${\mathfrak n}\subset {\mathfrak u}$
is a sum of root spaces and
![]() $\Delta ({\mathfrak n})$
denotes the corresponding set of positive roots. Unless otherwise stated, “a nilradical” (in
$\Delta ({\mathfrak n})$
denotes the corresponding set of positive roots. Unless otherwise stated, “a nilradical” (in
![]() ${\mathfrak g}$
) means “the nilradical of a standard parabolic subalgebra” of
${\mathfrak g}$
) means “the nilradical of a standard parabolic subalgebra” of
![]() ${\mathfrak g}$
. Let
${\mathfrak g}$
. Let ![]() be the Kostant cascade in
be the Kostant cascade in
![]() $\Delta ^+$
. It is a poset, and
$\Delta ^+$
. It is a poset, and
![]() $\beta _1=\theta $
is the unique maximal element of
$\beta _1=\theta $
is the unique maximal element of ![]() (see Section 2.2 for details). To each
(see Section 2.2 for details). To each
![]() ${\mathfrak n}$
, we attach the subposet
${\mathfrak n}$
, we attach the subposet ![]() . Another ingredient is the optimization of
. Another ingredient is the optimization of
![]() ${\mathfrak n}$
. By definition, it is the maximal nilradical,
${\mathfrak n}$
. By definition, it is the maximal nilradical,
![]() $\tilde {\mathfrak n}$
, such that
$\tilde {\mathfrak n}$
, such that ![]() . If
. If
![]() ${\mathfrak n}=\tilde {\mathfrak n}$
, then
${\mathfrak n}=\tilde {\mathfrak n}$
, then
![]() ${\mathfrak n}$
is said to be optimal. An explicit description of
${\mathfrak n}$
is said to be optimal. An explicit description of
![]() $\tilde {\mathfrak n}$
via
$\tilde {\mathfrak n}$
via ![]() is given in Section 2.3. Properties of the optimal nilradicals are better, and in order to approach arbitrary nilradicals, it is convenient to consider first the optimal ones. Roughly speaking, the output of this article is that to a great extent invariant-theoretic properties of
is given in Section 2.3. Properties of the optimal nilradicals are better, and in order to approach arbitrary nilradicals, it is convenient to consider first the optimal ones. Roughly speaking, the output of this article is that to a great extent invariant-theoretic properties of
![]() ${\mathfrak n}$
are determined by
${\mathfrak n}$
are determined by ![]() and
and
![]() $\tilde {\mathfrak n}$
.
$\tilde {\mathfrak n}$
.
1.2
Let
![]() ${\mathfrak q}={\mathrm {Lie\,}} Q$
be a Lie algebra. As usual,
${\mathfrak q}={\mathrm {Lie\,}} Q$
be a Lie algebra. As usual,
![]() $\xi \in {\mathfrak q}^{*}$
is said to be regular, if the stabilizer
$\xi \in {\mathfrak q}^{*}$
is said to be regular, if the stabilizer
![]() ${\mathfrak q}^{\xi }$
has minimal dimension. Then
${\mathfrak q}^{\xi }$
has minimal dimension. Then
![]() ${\mathfrak q}^{*}_{\mathsf {reg}}$
denotes the set of all regular points and
${\mathfrak q}^{*}_{\mathsf {reg}}$
denotes the set of all regular points and
![]() ${{\mathrm {ind}}\,{\mathfrak q}:=\dim {\mathfrak q}^{\xi }}$
for any
${{\mathrm {ind}}\,{\mathfrak q}:=\dim {\mathfrak q}^{\xi }}$
for any
![]() $\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
. If
$\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
. If
![]() ${\mathrm {ind}}\,{\mathfrak q}=0$
, then
${\mathrm {ind}}\,{\mathfrak q}=0$
, then
![]() ${\mathfrak q}$
is called Frobenius. Set
${\mathfrak q}$
is called Frobenius. Set
![]() $\boldsymbol {b}({\mathfrak q}):=(\dim {\mathfrak q}+{\mathrm {ind}}\,{\mathfrak q})/2$
. By definition, the Frobenius semiradical of
$\boldsymbol {b}({\mathfrak q}):=(\dim {\mathfrak q}+{\mathrm {ind}}\,{\mathfrak q})/2$
. By definition, the Frobenius semiradical of
![]() ${\mathfrak q}$
is
${\mathfrak q}$
is
![]() ${\mathcal F}({\mathfrak q})=\sum _{\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}}{\mathfrak q}^{\xi }$
. Hence,
${\mathcal F}({\mathfrak q})=\sum _{\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}}{\mathfrak q}^{\xi }$
. Hence,
![]() ${\mathcal F}({\mathfrak q})=0$
if and only if
${\mathcal F}({\mathfrak q})=0$
if and only if
![]() ${\mathfrak q}$
is Frobenius. Clearly,
${\mathfrak q}$
is Frobenius. Clearly,
![]() ${\mathcal F}({\mathfrak q})$
is a characteristic ideal of
${\mathcal F}({\mathfrak q})$
is a characteristic ideal of
![]() ${\mathfrak q}$
. This notion and basic results on it are due to Ooms [Reference Ooms18, Reference Ooms19].
${\mathfrak q}$
. This notion and basic results on it are due to Ooms [Reference Ooms18, Reference Ooms19].
The symmetric algebra of
![]() ${\mathfrak q}$
,
${\mathfrak q}$
, ![]() , is a Poisson algebra equipped with the Lie–Poisson bracket
, is a Poisson algebra equipped with the Lie–Poisson bracket
![]() $\{\ ,\,\}$
. The algebra of symmetric invariants
$\{\ ,\,\}$
. The algebra of symmetric invariants ![]() is the center of
is the center of ![]() , i.e.,
, i.e.,
If the group Q is connected, then ![]() , i.e., the Poisson center
, i.e., the Poisson center ![]() is also the algebra of Q-invariant polynomial functions on
is also the algebra of Q-invariant polynomial functions on
![]() ${\mathfrak q}^{*}$
. If
${\mathfrak q}^{*}$
. If ![]() is a Poisson-commutative subalgebra, then
is a Poisson-commutative subalgebra, then
![]() ${\mathrm {trdeg\,}}\mathcal P\leqslant \boldsymbol {b}({\mathfrak q})$
[Reference Vinberg28, 0.2] and this upper bound is always attained [Reference Sadetov25]. Therefore, if
${\mathrm {trdeg\,}}\mathcal P\leqslant \boldsymbol {b}({\mathfrak q})$
[Reference Vinberg28, 0.2] and this upper bound is always attained [Reference Sadetov25]. Therefore, if
![]() ${\mathfrak r}\subset {\mathfrak q}$
is a Lie subalgebra, then
${\mathfrak r}\subset {\mathfrak q}$
is a Lie subalgebra, then
![]() $\boldsymbol {b}({\mathfrak r})\leqslant \boldsymbol {b}({\mathfrak q})$
. The passage
$\boldsymbol {b}({\mathfrak r})\leqslant \boldsymbol {b}({\mathfrak q})$
. The passage
![]() ${\mathfrak n}\leadsto \tilde {\mathfrak n}$
has the property that
${\mathfrak n}\leadsto \tilde {\mathfrak n}$
has the property that
![]() $\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})$
. This implies that
$\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})$
. This implies that ![]() (see [Reference Panyushev22, Proposition 5.5]).
(see [Reference Panyushev22, Proposition 5.5]).
An abelian subalgebra
![]() ${\mathfrak a}\subset {\mathfrak q}$
is called a commutative polarization (= CP), if
${\mathfrak a}\subset {\mathfrak q}$
is called a commutative polarization (= CP), if
![]() ${\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})}$
. Then
${\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})}$
. Then
![]() $\boldsymbol {b}({\mathfrak a})=\boldsymbol {b}({\mathfrak q})$
. A complete classification of the nilradicals with CP is obtained in [Reference Panyushev22]. In Section 3.4, we use Rosenlicht’s theorem to provide simple proofs of some basic properties of CP’s.
$\boldsymbol {b}({\mathfrak a})=\boldsymbol {b}({\mathfrak q})$
. A complete classification of the nilradicals with CP is obtained in [Reference Panyushev22]. In Section 3.4, we use Rosenlicht’s theorem to provide simple proofs of some basic properties of CP’s.
1.3
For
![]() ${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
, let
${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
, let
![]() ${\mathfrak n}^-\subset {\mathfrak u}^-$
be the opposite nilradical, i.e.,
${\mathfrak n}^-\subset {\mathfrak u}^-$
be the opposite nilradical, i.e.,
![]() $\Delta ({\mathfrak n}^-)=-\Delta ({\mathfrak n})$
. Then
$\Delta ({\mathfrak n}^-)=-\Delta ({\mathfrak n})$
. Then
![]() ${\mathfrak g}={\mathfrak p}\oplus {\mathfrak n}^-$
. Let
${\mathfrak g}={\mathfrak p}\oplus {\mathfrak n}^-$
. Let
![]() ${\mathfrak g}_{\gamma }$
denote the roots space of
${\mathfrak g}_{\gamma }$
denote the roots space of
![]() $\gamma \in \Delta $
and
$\gamma \in \Delta $
and
![]() $e_{\gamma }\in {\mathfrak g}_{\gamma }$
a nonzero vector. Consider the space
$e_{\gamma }\in {\mathfrak g}_{\gamma }$
a nonzero vector. Consider the space ![]() and
and ![]() . Using the vector space isomorphism
. Using the vector space isomorphism
![]() ${\mathfrak n}^{*}={\mathfrak g}/{\mathfrak p}\simeq {\mathfrak n}^-$
, one can regard
${\mathfrak n}^{*}={\mathfrak g}/{\mathfrak p}\simeq {\mathfrak n}^-$
, one can regard
![]() ${\mathfrak k}$
as a subspace of
${\mathfrak k}$
as a subspace of
![]() ${\mathfrak n}^{*}$
and
${\mathfrak n}^{*}$
and
![]() ${\boldsymbol {\zeta }}$
as an element of
${\boldsymbol {\zeta }}$
as an element of
![]() ${\mathfrak n}^{*}$
. We say that
${\mathfrak n}^{*}$
. We say that
![]() ${\mathfrak k}\subset {\mathfrak n}^{*}$
is a cascade subspace and
${\mathfrak k}\subset {\mathfrak n}^{*}$
is a cascade subspace and
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}$
is a cascade point. As usual,
${\boldsymbol {\zeta }}\in {\mathfrak k}$
is a cascade point. As usual,
![]() $\xi \in {\mathfrak n}^{*}$
is called N-generic, if there is an open subset
$\xi \in {\mathfrak n}^{*}$
is called N-generic, if there is an open subset
![]() $\Omega \in {\mathfrak n}^{*}$
such that
$\Omega \in {\mathfrak n}^{*}$
such that
![]() $\xi \in \Omega $
and the stabilizer
$\xi \in \Omega $
and the stabilizer
![]() ${\mathfrak n}^{\xi }$
is N-conjugate to
${\mathfrak n}^{\xi }$
is N-conjugate to
![]() ${\mathfrak n}^{\xi '}$
for any
${\mathfrak n}^{\xi '}$
for any
![]() $\xi '\in \Omega $
. Any stabilizer
$\xi '\in \Omega $
. Any stabilizer
![]() ${\mathfrak n}^{\nu }$
with
${\mathfrak n}^{\nu }$
with
![]() $\nu \in \Omega $
is said to be N-generic, too.
$\nu \in \Omega $
is said to be N-generic, too.
In Section 4, we prove that the action
![]() $(N:{\mathfrak n}^{*})$
has N-generic stabilizers if and only if the stabilizer
$(N:{\mathfrak n}^{*})$
has N-generic stabilizers if and only if the stabilizer
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
is generic (and the latter is not always the case!). Moreover, N-generic stabilizers always exist if
${\mathfrak n}^{\boldsymbol {\zeta }}$
is generic (and the latter is not always the case!). Moreover, N-generic stabilizers always exist if
![]() ${\mathfrak n}$
is optimal. If
${\mathfrak n}$
is optimal. If
![]() ${\mathfrak n}$
is not optimal, then one can consider the linear action of the larger group
${\mathfrak n}$
is not optimal, then one can consider the linear action of the larger group
![]() $\tilde N=\exp (\tilde {\mathfrak n})\supset N$
on
$\tilde N=\exp (\tilde {\mathfrak n})\supset N$
on
![]() ${\mathfrak n}^{*}$
. We prove that the action
${\mathfrak n}^{*}$
. We prove that the action
![]() $(\tilde N:{\mathfrak n}^{*})$
always has an
$(\tilde N:{\mathfrak n}^{*})$
always has an
![]() $\tilde N$
-generic stabilizer, and
$\tilde N$
-generic stabilizer, and
![]() $\tilde {\mathfrak n}^{\boldsymbol {\zeta }}$
is such a stabilizer. Actually, the equality
$\tilde {\mathfrak n}^{\boldsymbol {\zeta }}$
is such a stabilizer. Actually, the equality
![]() $\tilde {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}^{\boldsymbol {\zeta }}$
holds here. For any
$\tilde {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}^{\boldsymbol {\zeta }}$
holds here. For any
![]() ${\mathfrak n}$
, we give an explicit formula for
${\mathfrak n}$
, we give an explicit formula for
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
via
${\mathfrak n}^{\boldsymbol {\zeta }}$
via ![]() and
and
![]() $\tilde {\mathfrak n}$
, which shows that
$\tilde {\mathfrak n}$
, which shows that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
is T-stable. Using that formula and the criterion for the coadjoint representations [Reference Tauvel and Yu27, Corollary 1.8(i)], one easily verifies whether the stabilizer
${\mathfrak n}^{\boldsymbol {\zeta }}$
is T-stable. Using that formula and the criterion for the coadjoint representations [Reference Tauvel and Yu27, Corollary 1.8(i)], one easily verifies whether the stabilizer
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
is generic in each concrete example. For
${\mathfrak n}^{\boldsymbol {\zeta }}$
is generic in each concrete example. For
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
, the nilradicals having a generic stabilizer for
${\mathsf {\mathbf {{A}}}}_{n}$
, the nilradicals having a generic stabilizer for
![]() $(N:{\mathfrak n}^{*})$
are explicitly described, while for
$(N:{\mathfrak n}^{*})$
are explicitly described, while for
![]() ${\mathsf {\mathbf {{C}}}}_{n}$
, all nilradicals have a generic stabilizer (see Section 5). A general construction of nilradicals without generic stabilizers is also provided.
${\mathsf {\mathbf {{C}}}}_{n}$
, all nilradicals have a generic stabilizer (see Section 5). A general construction of nilradicals without generic stabilizers is also provided.
We prove that
![]() ${\mathcal F}({\mathfrak n})$
is the
${\mathcal F}({\mathfrak n})$
is the
![]() ${\mathfrak b}$
-stable ideal of
${\mathfrak b}$
-stable ideal of
![]() ${\mathfrak n}$
generated by
${\mathfrak n}$
generated by
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
(regardless of the presence of generic stabilizers). Then our formula for
${\mathfrak n}^{\boldsymbol {\zeta }}$
(regardless of the presence of generic stabilizers). Then our formula for
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
allows us to explicitly describe
${\mathfrak n}^{\boldsymbol {\zeta }}$
allows us to explicitly describe
![]() ${\mathcal F}({\mathfrak n})$
for
${\mathcal F}({\mathfrak n})$
for
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
and
${\mathsf {\mathbf {{A}}}}_{n}$
and
![]() ${\mathsf {\mathbf {{C}}}}_{n}$
. For any
${\mathsf {\mathbf {{C}}}}_{n}$
. For any
![]() ${\mathfrak g}$
, we provide a criterion for the equality
${\mathfrak g}$
, we provide a criterion for the equality
![]() ${\mathcal F}({\mathfrak n})={\mathfrak n}$
and give the complete list of nilradicals with this property. Another observation is that if
${\mathcal F}({\mathfrak n})={\mathfrak n}$
and give the complete list of nilradicals with this property. Another observation is that if
![]() ${\mathfrak n}\subset {\mathfrak n}'\subset \tilde {\mathfrak n}$
, then
${\mathfrak n}\subset {\mathfrak n}'\subset \tilde {\mathfrak n}$
, then
![]() ${\mathcal F}({\mathfrak n}')\subset {\mathcal F}({\mathfrak n})$
.
${\mathcal F}({\mathfrak n}')\subset {\mathcal F}({\mathfrak n})$
.
1.4
Since
![]() ${\mathfrak n}$
is B-stable, one can consider the algebra of Q-invariants
${\mathfrak n}$
is B-stable, one can consider the algebra of Q-invariants ![]() for any subgroup
for any subgroup
![]() $Q\subset B$
, and we are primarily interested in the unipotent subgroups U and
$Q\subset B$
, and we are primarily interested in the unipotent subgroups U and
![]() $\tilde N=\exp (\tilde {\mathfrak n})\subset U$
. In Section 6, we prove that
$\tilde N=\exp (\tilde {\mathfrak n})\subset U$
. In Section 6, we prove that
and this common algebra is polynomial, of Krull dimension ![]() . In particular, for any optimal nilradical
. In particular, for any optimal nilradical
![]() $\tilde {\mathfrak n}$
, the Poisson center of
$\tilde {\mathfrak n}$
, the Poisson center of ![]() is a polynomial algebra. If
is a polynomial algebra. If
![]() ${\mathfrak n}\ne \tilde {\mathfrak n}$
, then
${\mathfrak n}\ne \tilde {\mathfrak n}$
, then ![]() does not occur in (1.1). This algebra is not always polynomial, and its Krull dimension equals
does not occur in (1.1). This algebra is not always polynomial, and its Krull dimension equals ![]() . Nevertheless,
. Nevertheless, ![]() shares many properties with algebras of invariants of reductive groups. For instance,
shares many properties with algebras of invariants of reductive groups. For instance, ![]() is finitely generated [Reference Joseph12, Lemma 4.6], and we prove that the affine variety
is finitely generated [Reference Joseph12, Lemma 4.6], and we prove that the affine variety ![]() has rational singularities.
has rational singularities.
Using results on ![]() and
and
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
, we describe the nilradicals having the property that
${\mathfrak n}^{\boldsymbol {\zeta }}$
, we describe the nilradicals having the property that
![]() ${\mathrm {ind}}\,{\mathfrak n}=\dim {\mathfrak z}({\mathfrak n})$
, where
${\mathrm {ind}}\,{\mathfrak n}=\dim {\mathfrak z}({\mathfrak n})$
, where
![]() ${\mathfrak z}({\mathfrak n})$
is the center of
${\mathfrak z}({\mathfrak n})$
is the center of
![]() ${\mathfrak n}$
. By [Reference Moore and Wolf15], this property is equivalent to that the Lie group N has a “square integrable representation.” Therefore, such nilpotent Lie algebras are sometimes called “square integrable” (see [Reference Elashvili9, Reference Elashvili and Ooms10]). From a modern point of view, the square integrable nilradicals are precisely the “quasi-reductive” ones (see [Reference Baur and Moreau1, Reference Duflo, Khalgui and Torasso7, Reference Moreau and Yakimova16]). Our description shows that all square integrable nilradicals are metabelian.
${\mathfrak n}$
. By [Reference Moore and Wolf15], this property is equivalent to that the Lie group N has a “square integrable representation.” Therefore, such nilpotent Lie algebras are sometimes called “square integrable” (see [Reference Elashvili9, Reference Elashvili and Ooms10]). From a modern point of view, the square integrable nilradicals are precisely the “quasi-reductive” ones (see [Reference Baur and Moreau1, Reference Duflo, Khalgui and Torasso7, Reference Moreau and Yakimova16]). Our description shows that all square integrable nilradicals are metabelian.
As ![]() is a polynomial algebra, we are interested in question whether
is a polynomial algebra, we are interested in question whether ![]() is a free
is a free ![]() -module. Equivalently, when is the quotient map
-module. Equivalently, when is the quotient map ![]() equidimensional? We prove several assertions for U or (what is the same)
equidimensional? We prove several assertions for U or (what is the same)
![]() $\tilde N$
.
$\tilde N$
.
• If
![]() ${\mathfrak n}$
has a CP, then
${\mathfrak n}$
has a CP, then ![]() is a free module over
is a free module over ![]() . This includes all nilradicals for
. This includes all nilradicals for
![]() ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
or
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
or
![]() ${\mathfrak {sp}}_{2n}$
.
${\mathfrak {sp}}_{2n}$
.
• In particular, if
![]() ${\mathfrak n}$
is the optimization of a nilradical with CP (any
${\mathfrak n}$
is the optimization of a nilradical with CP (any
![]() ${\mathfrak g}$
) or any optimal nilradical in
${\mathfrak g}$
) or any optimal nilradical in
![]() ${\mathfrak {sl}}_{n+1}$
or
${\mathfrak {sl}}_{n+1}$
or
![]() ${\mathfrak {sp}}_{2n}$
, then
${\mathfrak {sp}}_{2n}$
, then ![]() is a free module over its Poisson center
is a free module over its Poisson center ![]() . This also implies that in these cases, the enveloping algebra
. This also implies that in these cases, the enveloping algebra ![]() is a free module over its center.
is a free module over its center.
1.5 Structure of the article
In Section 2, we recall basic facts on ![]() and (optimal) nilradicals. In Section 3, the necessary information is gathered on generic stabilizers, the Frobenius semiradical, and commutative polarizations. We also include invariant-theoretic proofs for some properties of commutative polarizations. Our results on generic stabilizers and
and (optimal) nilradicals. In Section 3, the necessary information is gathered on generic stabilizers, the Frobenius semiradical, and commutative polarizations. We also include invariant-theoretic proofs for some properties of commutative polarizations. Our results on generic stabilizers and
![]() ${\mathcal F}({\mathfrak n})$
for a nilradical
${\mathcal F}({\mathfrak n})$
for a nilradical
![]() ${\mathfrak n}\subset {\mathfrak g}$
are gathered in Section 4, whereas Section 5 contains explicit results for
${\mathfrak n}\subset {\mathfrak g}$
are gathered in Section 4, whereas Section 5 contains explicit results for
![]() ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
or
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
or
![]() ${\mathfrak {sp}}_{2n}$
. In Section 6, we study various algebras of invariants related to the coadjoint representation of
${\mathfrak {sp}}_{2n}$
. In Section 6, we study various algebras of invariants related to the coadjoint representation of
![]() ${\mathfrak n}$
, and in Section 7, we classify the square integrable nilradicals. Topics related to the equidimensionality of the quotient map
${\mathfrak n}$
, and in Section 7, we classify the square integrable nilradicals. Topics related to the equidimensionality of the quotient map
![]() $\pi :{\mathfrak n}^{*}\to {\mathfrak n}^{*}/\!\!/ U$
are treated in Section 8. The lists of cascade roots for all
$\pi :{\mathfrak n}^{*}\to {\mathfrak n}^{*}/\!\!/ U$
are treated in Section 8. The lists of cascade roots for all
![]() ${\mathfrak g}$
and the Hasse diagrams of some posets
${\mathfrak g}$
and the Hasse diagrams of some posets ![]() are presented in Appendix A.
are presented in Appendix A.
Main notation. Throughout,
![]() ${\mathfrak g}={\mathrm {Lie\,}}(G)$
is a simple Lie algebra. Then:
${\mathfrak g}={\mathrm {Lie\,}}(G)$
is a simple Lie algebra. Then:
-
–
 ${\mathfrak b}$
is a fixed Borel subalgebra of
${\mathfrak b}$
is a fixed Borel subalgebra of
 ${\mathfrak g}$
with
${\mathfrak g}$
with
 ${\mathfrak u}=[{\mathfrak b},{\mathfrak b}]$
.
${\mathfrak u}=[{\mathfrak b},{\mathfrak b}]$
. -
–
 ${\mathfrak t}$
is a fixed Cartan subalgebra in
${\mathfrak t}$
is a fixed Cartan subalgebra in
 ${\mathfrak b}$
and
${\mathfrak b}$
and
 $\Delta $
is the root system of
$\Delta $
is the root system of
 ${\mathfrak g}$
with respect to
${\mathfrak g}$
with respect to
 ${\mathfrak t}$
.
${\mathfrak t}$
. -
–
 $\Delta ^+$
is the set positive roots corresponding to
$\Delta ^+$
is the set positive roots corresponding to
 ${\mathfrak u}$
, and
${\mathfrak u}$
, and
 $\theta \in \Delta ^+$
is the highest root.
$\theta \in \Delta ^+$
is the highest root. -
–
 $\Pi =\{\alpha _1,\dots ,\alpha _{{\mathsf {rk\,}}{\mathfrak g}}\}$
is the set of simple roots in
$\Pi =\{\alpha _1,\dots ,\alpha _{{\mathsf {rk\,}}{\mathfrak g}}\}$
is the set of simple roots in
 $\Delta ^+$
.
$\Delta ^+$
. -
–
 ${\mathfrak t}^{*}_{\mathbb Q}$
is the
${\mathfrak t}^{*}_{\mathbb Q}$
is the
 ${\mathbb Q}$
-vector subspace of
${\mathbb Q}$
-vector subspace of
 ${\mathfrak t}^{*}$
spanned by
${\mathfrak t}^{*}$
spanned by
 $\Delta $
, and
$\Delta $
, and
 $(\ ,\, )$
is the positive-definite form on
$(\ ,\, )$
is the positive-definite form on
 ${\mathfrak t}^{*}_{\mathbb Q}$
induced by the Killing form on
${\mathfrak t}^{*}_{\mathbb Q}$
induced by the Killing form on
 ${\mathfrak g}$
.
${\mathfrak g}$
. -
– If
 $\gamma \in \Delta $
, then
$\gamma \in \Delta $
, then
 ${\mathfrak g}_{\gamma }$
is the root space in
${\mathfrak g}_{\gamma }$
is the root space in
 ${\mathfrak g}$
and
${\mathfrak g}$
and
 $e_{\gamma }\in {\mathfrak g}_{\gamma }$
is a nonzero vector.
$e_{\gamma }\in {\mathfrak g}_{\gamma }$
is a nonzero vector. -
– If
 ${\mathfrak c}\subset {\mathfrak u}^{\pm }$
is a
${\mathfrak c}\subset {\mathfrak u}^{\pm }$
is a
 ${\mathfrak t}$
-stable subspace, then
${\mathfrak t}$
-stable subspace, then
 $\Delta ({\mathfrak c})\subset \Delta ^{\pm }$
is the set of roots of
$\Delta ({\mathfrak c})\subset \Delta ^{\pm }$
is the set of roots of
 ${\mathfrak c}$
.
${\mathfrak c}$
. -
–
 $\boldsymbol {b}({\mathfrak q})=(\dim {\mathfrak q}+{\mathrm {ind}}\,{\mathfrak q})/2$
for a Lie algebra
$\boldsymbol {b}({\mathfrak q})=(\dim {\mathfrak q}+{\mathrm {ind}}\,{\mathfrak q})/2$
for a Lie algebra
 ${\mathfrak q}$
.
${\mathfrak q}$
. -
– In the explicit examples, the Vinberg–Onishchik numbering of simple roots of
 ${\mathfrak g}$
is used (see [Reference Onishchik and Vinberg17, Table 1]).
${\mathfrak g}$
is used (see [Reference Onishchik and Vinberg17, Table 1]).
2 Generalities on the cascade and nilradicals
2.1 The root order in
 $\Delta ^+$
and the Heisenberg subset
$\Delta ^+$
and the Heisenberg subset
We identify
![]() $\Pi $
with the vertices of the Dynkin diagram of
$\Pi $
with the vertices of the Dynkin diagram of
![]() ${\mathfrak g}$
. For any
${\mathfrak g}$
. For any
![]() $\gamma \in \Delta ^+$
, let
$\gamma \in \Delta ^+$
, let
![]() $[\gamma :\alpha ]$
be the coefficient of
$[\gamma :\alpha ]$
be the coefficient of
![]() $\alpha \in \Pi $
in the expression of
$\alpha \in \Pi $
in the expression of
![]() $\gamma $
via
$\gamma $
via
![]() $\Pi $
. The support of
$\Pi $
. The support of
![]() $\gamma $
is
$\gamma $
is
![]() ${\mathsf {supp}}(\gamma )=\{\alpha \in \Pi \mid [\gamma :\alpha ]\ne 0\}$
. As is well known,
${\mathsf {supp}}(\gamma )=\{\alpha \in \Pi \mid [\gamma :\alpha ]\ne 0\}$
. As is well known,
![]() ${\mathsf {supp}}(\gamma )$
is a connected subset of the Dynkin diagram. For instance,
${\mathsf {supp}}(\gamma )$
is a connected subset of the Dynkin diagram. For instance,
![]() ${\mathsf {supp}}(\theta )=\Pi $
and
${\mathsf {supp}}(\theta )=\Pi $
and
![]() ${\mathsf {supp}}(\alpha )=\{\alpha \}$
. Let “
${\mathsf {supp}}(\alpha )=\{\alpha \}$
. Let “
![]() $\preccurlyeq $
” denote the root order in
$\preccurlyeq $
” denote the root order in
![]() $\Delta ^+$
, i.e., we set
$\Delta ^+$
, i.e., we set
![]() $\gamma \preccurlyeq \gamma '$
if
$\gamma \preccurlyeq \gamma '$
if
![]() $[\gamma :\alpha ]\leqslant [\gamma ':\alpha ]$
for all
$[\gamma :\alpha ]\leqslant [\gamma ':\alpha ]$
for all
![]() $\alpha \in \Pi $
. Then
$\alpha \in \Pi $
. Then
![]() $(\Delta ^+,\preccurlyeq )$
is a graded poset, and we write
$(\Delta ^+,\preccurlyeq )$
is a graded poset, and we write
![]() $\gamma \prec \gamma '$
if
$\gamma \prec \gamma '$
if
![]() $\gamma \preccurlyeq \gamma '$
and
$\gamma \preccurlyeq \gamma '$
and
![]() $\gamma \ne \gamma '$
.
$\gamma \ne \gamma '$
.
An upper ideal of
![]() $(\Delta ^+,\preccurlyeq )$
is a subset I such that if
$(\Delta ^+,\preccurlyeq )$
is a subset I such that if
![]() $\gamma \in I$
and
$\gamma \in I$
and
![]() $\gamma \prec \gamma '$
, then
$\gamma \prec \gamma '$
, then
![]() $\gamma '\in I$
. Therefore, I is an upper ideal of
$\gamma '\in I$
. Therefore, I is an upper ideal of
![]() $\Delta ^+$
if and only if
$\Delta ^+$
if and only if
![]() ${\mathfrak r}=\bigoplus _{\gamma \in I} {\mathfrak g}_{\gamma }$
is a
${\mathfrak r}=\bigoplus _{\gamma \in I} {\mathfrak g}_{\gamma }$
is a
![]() ${\mathfrak b}$
-stable ideal of
${\mathfrak b}$
-stable ideal of
![]() ${\mathfrak u}$
, i.e.,
${\mathfrak u}$
, i.e.,
![]() $[{\mathfrak b},{\mathfrak r}]\subset {\mathfrak r}$
.
$[{\mathfrak b},{\mathfrak r}]\subset {\mathfrak r}$
.
For a dominant weight
![]() $\lambda \in {\mathfrak t}^{*}_{\mathbb Q}$
, set
$\lambda \in {\mathfrak t}^{*}_{\mathbb Q}$
, set
![]() $\Delta _{\lambda }=\{\gamma \in \Delta \mid (\lambda ,\gamma )=0 \}$
and
$\Delta _{\lambda }=\{\gamma \in \Delta \mid (\lambda ,\gamma )=0 \}$
and
![]() $\Delta ^{\pm }_{\lambda }=\Delta _{\lambda }\cap \Delta ^{\pm }$
. Then
$\Delta ^{\pm }_{\lambda }=\Delta _{\lambda }\cap \Delta ^{\pm }$
. Then
![]() $\Delta _{\lambda }$
is the root system of a semisimple subalgebra
$\Delta _{\lambda }$
is the root system of a semisimple subalgebra
![]() ${\mathfrak g}^{\perp \lambda }\subset {\mathfrak g}$
and
${\mathfrak g}^{\perp \lambda }\subset {\mathfrak g}$
and
![]() $\Pi _{\lambda }=\Pi \cap \Delta ^+_{\lambda }$
is the set of simple roots in
$\Pi _{\lambda }=\Pi \cap \Delta ^+_{\lambda }$
is the set of simple roots in
![]() $\Delta ^+_{\lambda }$
. Then:
$\Delta ^+_{\lambda }$
. Then:
-
•
 ${\mathfrak p}_{\lambda }={\mathfrak g}^{\perp \lambda }+{\mathfrak b}$
is a standard parabolic subalgebra of
${\mathfrak p}_{\lambda }={\mathfrak g}^{\perp \lambda }+{\mathfrak b}$
is a standard parabolic subalgebra of
 ${\mathfrak g}$
.
${\mathfrak g}$
. -
• The set of roots of the nilradical
 ${\mathfrak n}_{\lambda }={\mathfrak p}_{\lambda }^{\mathsf {nil}}$
is
${\mathfrak n}_{\lambda }={\mathfrak p}_{\lambda }^{\mathsf {nil}}$
is
 $\Delta ^+\setminus \Delta ^+_{\lambda }$
. It is also denoted by
$\Delta ^+\setminus \Delta ^+_{\lambda }$
. It is also denoted by
 $\Delta ({\mathfrak n}_{\lambda })$
.
$\Delta ({\mathfrak n}_{\lambda })$
.
If
![]() $\lambda =\theta $
, then
$\lambda =\theta $
, then
![]() ${\mathfrak n}_{\theta }$
is a Heisenberg Lie algebra (Heisenberg nilradical) and
${\mathfrak n}_{\theta }$
is a Heisenberg Lie algebra (Heisenberg nilradical) and ![]() is called the Heisenberg subset (of
is called the Heisenberg subset (of
![]() $\Delta ^+$
).
$\Delta ^+$
).
2.2 The cascade poset
The recursive construction of the Kostant cascade in
![]() $\Delta ^+$
begins with
$\Delta ^+$
begins with
![]() $\beta _1=\theta $
. On the next step, we take the highest roots in the irreducible subsystems of
$\beta _1=\theta $
. On the next step, we take the highest roots in the irreducible subsystems of
![]() $\Delta _{\theta }$
. These roots are called the descendants of
$\Delta _{\theta }$
. These roots are called the descendants of
![]() $\beta _1$
. The same construction is then applied to every descendant of
$\beta _1$
. The same construction is then applied to every descendant of
![]() $\beta _1$
, and so on. This procedure eventually terminates and yields a set
$\beta _1$
, and so on. This procedure eventually terminates and yields a set ![]() , which is called the Kostant cascade. The roots in
, which is called the Kostant cascade. The roots in ![]() are strongly orthogonal, which means that
are strongly orthogonal, which means that
![]() $\beta _i\pm \beta _j\not \in \Delta $
for all
$\beta _i\pm \beta _j\not \in \Delta $
for all
![]() $i,j$
. We make
$i,j$
. We make ![]() a poset by letting that
a poset by letting that
![]() $\beta _i$
covers
$\beta _i$
covers
![]() $\beta _j$
if and only if
$\beta _j$
if and only if
![]() $\beta _j$
is a descendant of
$\beta _j$
is a descendant of
![]() $\beta _i$
. Then
$\beta _i$
. Then
![]() $\beta _1$
is the unique maximal element of
$\beta _1$
is the unique maximal element of ![]() . We refer to [Reference Joseph12, Section 2], [Reference Kostant13], and [Reference Panyushev22, 2.2] for more details. Let us summarize the main features of
. We refer to [Reference Joseph12, Section 2], [Reference Kostant13], and [Reference Panyushev22, 2.2] for more details. Let us summarize the main features of ![]() .
.
-
•
 is a maximal set of strongly orthogonal roots in
is a maximal set of strongly orthogonal roots in
 $\Delta ^+$
.
$\Delta ^+$
. -
• Each
 $\beta _i$
is the highest root of the irreducible root system
$\beta _i$
is the highest root of the irreducible root system
 $\Delta \langle i\rangle \subset \Delta $
with simple roots
$\Delta \langle i\rangle \subset \Delta $
with simple roots
 ${\mathsf {supp}}(\beta _i)$
.
${\mathsf {supp}}(\beta _i)$
. -
•
 is also a subposet of
is also a subposet of
 $(\Delta ^+,\preccurlyeq )$
, which provides the same poset structure as above.
$(\Delta ^+,\preccurlyeq )$
, which provides the same poset structure as above. -
• One has
 $\beta _j\prec \beta _i$
if and only if
$\beta _j\prec \beta _i$
if and only if
 ${\mathsf {supp}}(\beta _j)\varsubsetneq {\mathsf {supp}}(\beta _i)$
.
${\mathsf {supp}}(\beta _j)\varsubsetneq {\mathsf {supp}}(\beta _i)$
. -
•
 $\beta _j$
and
$\beta _j$
and
 $\beta _i$
are incomparable in
$\beta _i$
are incomparable in  if and only if
if and only if
 ${\mathsf {supp}}(\beta _j)\cap {\mathsf {supp}}(\beta _i)=\varnothing $
.
${\mathsf {supp}}(\beta _j)\cap {\mathsf {supp}}(\beta _i)=\varnothing $
. -
• The numbering of
 is not canonical. It is only required to be a linear extension of
is not canonical. It is only required to be a linear extension of  , i.e., if
, i.e., if
 $\beta _j\prec \beta _i$
, then
$\beta _j\prec \beta _i$
, then
 $j>i$
. In specific examples considered below, we use the numbering of cascade roots given in Appendix A.
$j>i$
. In specific examples considered below, we use the numbering of cascade roots given in Appendix A.
Using the decomposition ![]() and induction on
and induction on
![]() ${\mathsf {rk\,}}{\mathfrak g}$
, one obtains the disjoint union parametrized by
${\mathsf {rk\,}}{\mathfrak g}$
, one obtains the disjoint union parametrized by ![]() :
:
where ![]() is the Heisenberg subset of
is the Heisenberg subset of
![]() $\Delta \langle i\rangle ^+$
and
$\Delta \langle i\rangle ^+$
and ![]() . For
. For
![]() $1\leqslant i\leqslant m$
, let
$1\leqslant i\leqslant m$
, let
![]() ${\mathfrak g}\langle i\rangle \subset {\mathfrak g}$
be the simple Lie algebra with root system
${\mathfrak g}\langle i\rangle \subset {\mathfrak g}$
be the simple Lie algebra with root system
![]() $\Delta \langle i\rangle $
. The geometric counterpart of (2.1) is the vector space sum
$\Delta \langle i\rangle $
. The geometric counterpart of (2.1) is the vector space sum
![]() ${\mathfrak u}=\bigoplus _{i=1}^m {\mathfrak h}_i$
, where
${\mathfrak u}=\bigoplus _{i=1}^m {\mathfrak h}_i$
, where
![]() ${\mathfrak h}_i$
is the Heisenberg Lie algebra in
${\mathfrak h}_i$
is the Heisenberg Lie algebra in
![]() ${\mathfrak g}\langle i\rangle $
and
${\mathfrak g}\langle i\rangle $
and ![]() . In particular,
. In particular,
![]() ${\mathfrak h}_1={\mathfrak n}_{\theta }$
. For each
${\mathfrak h}_1={\mathfrak n}_{\theta }$
. For each ![]() , we set
, we set ![]() . It then follows from (2.1) that
. It then follows from (2.1) that ![]() . Note that
. Note that
![]() $\#\Phi (\beta _i)\leqslant 2$
and
$\#\Phi (\beta _i)\leqslant 2$
and
![]() $\#\Phi (\beta _i)= 2$
if and only if the algebra
$\#\Phi (\beta _i)= 2$
if and only if the algebra
![]() ${\mathfrak g}\langle i\rangle $
is of type
${\mathfrak g}\langle i\rangle $
is of type
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
with
${\mathsf {\mathbf {{A}}}}_{n}$
with
![]() $n\geqslant 2$
. Our definition of the subsets
$n\geqslant 2$
. Our definition of the subsets
![]() $\Phi (\beta _i)$
yields the well-defined map
$\Phi (\beta _i)$
yields the well-defined map ![]() , where
, where
![]() $\Phi ^{-1}(\alpha )=\beta _i$
if
$\Phi ^{-1}(\alpha )=\beta _i$
if
![]() $\alpha \in \Phi (\beta _i)$
. Note that
$\alpha \in \Phi (\beta _i)$
. Note that
![]() $\alpha \in {\mathsf {supp}}(\Phi ^{-1}(\alpha ))$
and
$\alpha \in {\mathsf {supp}}(\Phi ^{-1}(\alpha ))$
and
![]() $\alpha \in \Phi (\Phi ^{-1}(\alpha ))$
. We think of the cascade poset as a triple
$\alpha \in \Phi (\Phi ^{-1}(\alpha ))$
. We think of the cascade poset as a triple ![]() . The corresponding Hasse diagrams, with subsets
. The corresponding Hasse diagrams, with subsets
![]() $\Phi (\beta _i)$
attached to every node, are depicted in [Reference Panyushev22, Section 6]. Some of them are included in Appendix A.
$\Phi (\beta _i)$
attached to every node, are depicted in [Reference Panyushev22, Section 6]. Some of them are included in Appendix A.
Obviously, ![]() , and
, and ![]() if and only if each
if and only if each
![]() $\beta _i$
is a multiple of a fundamental weight for
$\beta _i$
is a multiple of a fundamental weight for
![]() ${\mathfrak g}\langle i\rangle $
. Recall that
${\mathfrak g}\langle i\rangle $
. Recall that
![]() $\theta $
is a multiple of a fundamental weight of
$\theta $
is a multiple of a fundamental weight of
![]() ${\mathfrak g}$
if and only if
${\mathfrak g}$
if and only if
![]() ${\mathfrak g}$
is not of type
${\mathfrak g}$
is not of type
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
,
${\mathsf {\mathbf {{A}}}}_{n}$
,
![]() $n\geqslant 2$
. It is well known that
$n\geqslant 2$
. It is well known that ![]() if and only if
if and only if
![]() ${\mathrm {ind}}\,{\mathfrak b}=0$
. This happens exactly if
${\mathrm {ind}}\,{\mathfrak b}=0$
. This happens exactly if
![]() ${\mathfrak g}\not \in \{{\mathsf {\mathbf {{A}}}}_{n}, {\mathsf {\mathbf {{D}}}}_{2n+1}, {\mathsf {\mathbf {{E}}}}_{6}\}$
and then
${\mathfrak g}\not \in \{{\mathsf {\mathbf {{A}}}}_{n}, {\mathsf {\mathbf {{D}}}}_{2n+1}, {\mathsf {\mathbf {{E}}}}_{6}\}$
and then
![]() $\Phi ^{-1}$
yields a bijection between
$\Phi ^{-1}$
yields a bijection between ![]() and
and
![]() $\Pi $
.
$\Pi $
.
2.3 Nilradicals and optimal nilradicals
Let
![]() ${\mathfrak p}\supset {\mathfrak b}$
be a standard parabolic subalgebra of
${\mathfrak p}\supset {\mathfrak b}$
be a standard parabolic subalgebra of
![]() ${\mathfrak g}$
, with nilradical
${\mathfrak g}$
, with nilradical
![]() ${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
. If
${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
. If ![]() , then we write
, then we write ![]() and
and ![]() . Here,
. Here, ![]() is the set of minimal elements of the poset
is the set of minimal elements of the poset
![]() $(\Delta ({\mathfrak n}), \preccurlyeq )$
and
$(\Delta ({\mathfrak n}), \preccurlyeq )$
and ![]() is the set of simple roots for the standard Levi subalgebra
is the set of simple roots for the standard Levi subalgebra ![]() . Clearly,
. Clearly, ![]() if and only if
if and only if ![]() .
.
The integer ![]() is the depth of
is the depth of ![]() . Letting
. Letting

one obtains the partition ![]() and the canonical
and the canonical
![]() ${\mathbb Z}$
-grading
${\mathbb Z}$
-grading

The following is well known and easy.
Lemma 2.1 If ![]() denotes the lower central series of
denotes the lower central series of ![]() , then
, then ![]() . The center of
. The center of ![]() is
is ![]() . Hence,
. Hence, ![]() is abelian if and only if
is abelian if and only if ![]() , i.e.,
, i.e., ![]() and
and
![]() $[\theta :\alpha ]=1$
.
$[\theta :\alpha ]=1$
.
Set ![]() . Then
. Then ![]() for any nonzero nilradical
for any nonzero nilradical ![]() .
.
A standard parabolic subalgebra ![]() is said to be optimal if
is said to be optimal if
This goes back to [Reference Joseph12, 4.10], and we also apply this term to ![]() . Then
. Then ![]() is optimal if and only if
is optimal if and only if ![]() . For a nonempty
. For a nonempty ![]() , set
, set ![]() and consider the nilradical
and consider the nilradical ![]() . Then
. Then ![]() and
and ![]() . Hence,
. Hence, ![]() is optimal, it is the minimal optimal nilradical containing
is optimal, it is the minimal optimal nilradical containing ![]() , and it is the maximal element of the set of nilradicals
, and it is the maximal element of the set of nilradicals ![]() .
.
Definition 1 The nilradical ![]() is called the optimization of
is called the optimization of ![]() .
.
If ![]() is not specified for a given nilradical
is not specified for a given nilradical
![]() ${\mathfrak n}$
, then
${\mathfrak n}$
, then ![]() and we write
and we write
![]() $\tilde {\mathfrak n}$
for the optimization of
$\tilde {\mathfrak n}$
for the optimization of
![]() ${\mathfrak n}$
.
${\mathfrak n}$
.
Proposition 2.3 (cf. [Reference Joseph12, 2.4] and [Reference Panyushev22, 2.3])
Let
![]() $\tilde {\mathfrak n}$
be the optimization of a nilradical
$\tilde {\mathfrak n}$
be the optimization of a nilradical
![]() ${\mathfrak n}$
. Then:
${\mathfrak n}$
. Then:
-
•
 .
. -
•
 and
and
 $\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})$
.
$\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})$
.
Remark 2.4 The merit of optimization is that the passage from
![]() ${\mathfrak n}$
to
${\mathfrak n}$
to
![]() $\tilde {\mathfrak n}$
does not change
$\tilde {\mathfrak n}$
does not change ![]() and
and
![]() $\boldsymbol {b}({\mathfrak n})$
. More generally, if two nilradicals
$\boldsymbol {b}({\mathfrak n})$
. More generally, if two nilradicals
![]() ${\mathfrak n}'$
and
${\mathfrak n}'$
and
![]() ${\mathfrak n}$
have the same optimization, then
${\mathfrak n}$
have the same optimization, then ![]() and
and
![]() $\boldsymbol {b}({\mathfrak n}')=\boldsymbol {b}({\mathfrak n})$
. For instance, this happens if
$\boldsymbol {b}({\mathfrak n}')=\boldsymbol {b}({\mathfrak n})$
. For instance, this happens if
![]() ${\mathfrak n}\subset {\mathfrak n}'\subset \tilde {\mathfrak n}$
.
${\mathfrak n}\subset {\mathfrak n}'\subset \tilde {\mathfrak n}$
.
Example 2.5 (1) If
![]() ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
, then
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
, then
![]() ${\mathfrak u}$
is the set of strictly upper-triangular matrices,
${\mathfrak u}$
is the set of strictly upper-triangular matrices,
![]() $\alpha _i=\varepsilon _i-\varepsilon _{i+1}$
(
$\alpha _i=\varepsilon _i-\varepsilon _{i+1}$
(
![]() $1\leqslant i\leqslant n$
), and
$1\leqslant i\leqslant n$
), and ![]() , where
, where
![]() $t=[(n+1)/2]$
and
$t=[(n+1)/2]$
and
![]() $\beta _i=\alpha _i+\dots +\alpha _{n+1-i}=\varepsilon _i-\varepsilon _{n+2-i}$
. Here,
$\beta _i=\alpha _i+\dots +\alpha _{n+1-i}=\varepsilon _i-\varepsilon _{n+2-i}$
. Here, ![]() is a chain and
is a chain and
![]() $\Phi (\beta _i)=\{\alpha _i,\alpha _{n+1-i}\}$
.
$\Phi (\beta _i)=\{\alpha _i,\alpha _{n+1-i}\}$
.
(2) Take ![]() and the nilradical
and the nilradical ![]() . Then
. Then ![]() and therefore
and therefore ![]() (cf. the matrices below).
(cf. the matrices below).

The cells with ball represent the cascade, and the thick lines depict the Heisenberg subset attached to an element of the cascade. By Proposition 2.3, we have
![]() ${\mathrm {ind}}\,\tilde {\mathfrak n}=2$
,
${\mathrm {ind}}\,\tilde {\mathfrak n}=2$
,
![]() ${\mathrm {ind}}\,{\mathfrak n}=6$
, and
${\mathrm {ind}}\,{\mathfrak n}=6$
, and
![]() $\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})=10$
.
$\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})=10$
.
Example 2.6 For a square matrix A, let
![]() $\hat A$
denote its transpose with respect to the antidiagonal. Choose the skew-symmetric form defining
$\hat A$
denote its transpose with respect to the antidiagonal. Choose the skew-symmetric form defining
![]() ${\mathfrak g}={\mathfrak {sp}}_{2n}\subset {\mathfrak {sl}}_{2n}$
such that
${\mathfrak g}={\mathfrak {sp}}_{2n}\subset {\mathfrak {sl}}_{2n}$
such that
 $$\begin{align*}{\mathfrak {sp}}_{2n}=\left\{ \begin{pmatrix} A & M \\ M' & -\hat A\end{pmatrix}\mid M=\hat M \ \& \ M'=\hat M'\right\} , \end{align*}$$
$$\begin{align*}{\mathfrak {sp}}_{2n}=\left\{ \begin{pmatrix} A & M \\ M' & -\hat A\end{pmatrix}\mid M=\hat M \ \& \ M'=\hat M'\right\} , \end{align*}$$
where
![]() $A,M,M'$
are
$A,M,M'$
are
![]() $n\times n$
matrices. Then
$n\times n$
matrices. Then
![]() ${\mathfrak u}$
(resp.
${\mathfrak u}$
(resp.
![]() ${\mathfrak t}$
) is the set of symplectic strictly upper triangular (resp. diagonal) matrices. Hence,
${\mathfrak t}$
) is the set of symplectic strictly upper triangular (resp. diagonal) matrices. Hence,
![]() ${\mathfrak t}=\{\mathsf {diag}(\varepsilon _1,\dots ,\varepsilon _n,-\varepsilon _n,\dots ,-\varepsilon _1)\mid \varepsilon _i\in {\mathbb C} \}$
. Recall that
${\mathfrak t}=\{\mathsf {diag}(\varepsilon _1,\dots ,\varepsilon _n,-\varepsilon _n,\dots ,-\varepsilon _1)\mid \varepsilon _i\in {\mathbb C} \}$
. Recall that
![]() $\alpha _i=\varepsilon _i-\varepsilon _{i+1}$
(
$\alpha _i=\varepsilon _i-\varepsilon _{i+1}$
(
![]() $i<n$
) and
$i<n$
) and
![]() $\alpha _n=2\varepsilon _n$
. Then
$\alpha _n=2\varepsilon _n$
. Then ![]() is a chain, where
is a chain, where
![]() $\beta _i=2\varepsilon _i$
and
$\beta _i=2\varepsilon _i$
and
![]() $\Phi (\beta _i)=\{\alpha _i\}$
for all i. Here,
$\Phi (\beta _i)=\{\alpha _i\}$
for all i. Here,
![]() ${\mathfrak n}_{\{\alpha _{n}\}}=\Big\{\Big(\begin {matrix} 0 & M \\ 0 & 0\end {matrix}\Big)\mid M=\hat M \Big\}$
is the nilradical of the maximal parabolic subalgebra with
${\mathfrak n}_{\{\alpha _{n}\}}=\Big\{\Big(\begin {matrix} 0 & M \\ 0 & 0\end {matrix}\Big)\mid M=\hat M \Big\}$
is the nilradical of the maximal parabolic subalgebra with ![]() . It is the only (standard) abelian nilradical in
. It is the only (standard) abelian nilradical in
![]() ${\mathfrak {sp}}_{2n}$
and
${\mathfrak {sp}}_{2n}$
and ![]() corresponds to the antidiagonal entries of M.
corresponds to the antidiagonal entries of M.
3 Generic stabilizers, the Frobenius semiradical, and commutative polarizations
Let Q be a connected algebraic group with
![]() ${\mathfrak q}={\mathrm {Lie\,}} Q$
. If
${\mathfrak q}={\mathrm {Lie\,}} Q$
. If
![]() $\rho :Q\to GL({\mathbb {V}})$
is a representation of Q, then the corresponding Q-action on
$\rho :Q\to GL({\mathbb {V}})$
is a representation of Q, then the corresponding Q-action on
![]() ${\mathbb {V}}$
is denoted by
${\mathbb {V}}$
is denoted by
![]() $(Q:{\mathbb {V}})$
. For
$(Q:{\mathbb {V}})$
. For
![]() $q\in Q$
and
$q\in Q$
and
![]() $v\in {\mathbb {V}}$
, we write
$v\in {\mathbb {V}}$
, we write
![]() $q{\cdot }v$
in place of
$q{\cdot }v$
in place of
![]() $\rho (q)v$
. Likewise,
$\rho (q)v$
. Likewise,
![]() $({\mathfrak q}:{\mathbb {V}})$
corresponds to
$({\mathfrak q}:{\mathbb {V}})$
corresponds to
![]() $d\rho :{\mathfrak q}\to {\mathfrak {gl}}({\mathbb {V}})$
.
$d\rho :{\mathfrak q}\to {\mathfrak {gl}}({\mathbb {V}})$
.
3.1 Generic stabilizers
Let
![]() $(Q:{\mathbb {V}})$
be a linear action. We say that
$(Q:{\mathbb {V}})$
be a linear action. We say that
![]() $v\in {\mathbb {V}}$
is Q-generic, if there is a dense open subset
$v\in {\mathbb {V}}$
is Q-generic, if there is a dense open subset
![]() $\Omega \subset {\mathbb {V}}$
such that
$\Omega \subset {\mathbb {V}}$
such that
![]() $v\in \Omega $
and the stabilizer
$v\in \Omega $
and the stabilizer
![]() ${\mathfrak q}^x$
is Q-conjugate to
${\mathfrak q}^x$
is Q-conjugate to
![]() ${\mathfrak q}^v$
for any
${\mathfrak q}^v$
for any
![]() $x\in \Omega $
. Then any
$x\in \Omega $
. Then any
![]() ${\mathfrak q}^x$
(
${\mathfrak q}^x$
(
![]() $x\in \Omega )$
is called a Q-generic stabilizer for the representation
$x\in \Omega )$
is called a Q-generic stabilizer for the representation
![]() $({\mathfrak q}:{\mathbb {V}})$
, and we say that
$({\mathfrak q}:{\mathbb {V}})$
, and we say that
![]() $({\mathfrak q}: {\mathbb {V}})$
has a Q-generic stabilizer. (One can consider similar notions for non-connected groups, for arbitrary actions of Q, and for stationary subgroups
$({\mathfrak q}: {\mathbb {V}})$
has a Q-generic stabilizer. (One can consider similar notions for non-connected groups, for arbitrary actions of Q, and for stationary subgroups
![]() $Q^x\subset Q$
, but we do need it now.) By semi-continuity of orbit dimensions, the set Q-generic points is contained in the set of Q-regular points
$Q^x\subset Q$
, but we do need it now.) By semi-continuity of orbit dimensions, the set Q-generic points is contained in the set of Q-regular points
but usually, this inclusion is proper. By a result of Richardson [Reference Richardson24], if Q is reductive, then Q-generic stabilizers exist for any action of Q on a smooth affine variety. But this is no longer true for non-reductive groups, and one of our goals is to study (the presence of) generic stabilizers for the coadjoint representation of a nilradical in
![]() ${\mathfrak g}$
.
${\mathfrak g}$
.
A practical method for proving the existence of Q-generic points and finding Q-generic stabilizers is given by Elashvili [Reference Elashvili8, Lemma 1]. Let
![]() $\mathsf {T}_v(Q{\cdot }v)={\mathfrak q}{\cdot }v$
be the tangent space of the orbit
$\mathsf {T}_v(Q{\cdot }v)={\mathfrak q}{\cdot }v$
be the tangent space of the orbit
![]() $Q{\cdot }v$
at v and
$Q{\cdot }v$
at v and
![]() ${\mathbb {V}}^{{\mathfrak q}_v}$
the fixed point subspace of
${\mathbb {V}}^{{\mathfrak q}_v}$
the fixed point subspace of
![]() ${\mathfrak q}^v$
in
${\mathfrak q}^v$
in
![]() ${\mathbb {V}}$
. Then
${\mathbb {V}}$
. Then
The main case of interest for us is the coadjoint representation of Q, when
![]() ${\mathbb {V}}={\mathfrak q}^{*}$
. For the coadjoint representation, we usually skip “Q” from notation and refer to “generic” and “regular” points (in
${\mathbb {V}}={\mathfrak q}^{*}$
. For the coadjoint representation, we usually skip “Q” from notation and refer to “generic” and “regular” points (in
![]() ${\mathfrak q}^{*}$
) and “generic” stabilizers (in
${\mathfrak q}^{*}$
) and “generic” stabilizers (in
![]() ${\mathfrak q}$
). Translating Elashvili’s criterion (3.2) into the setting of coadjoint representations and taking annihilators, one obtains the following nice formula (see [Reference Tauvel and Yu27, Corollary 1.8(i)]). Given
${\mathfrak q}$
). Translating Elashvili’s criterion (3.2) into the setting of coadjoint representations and taking annihilators, one obtains the following nice formula (see [Reference Tauvel and Yu27, Corollary 1.8(i)]). Given
![]() $\xi \in {\mathfrak q}^{*}$
, the stabilizer
$\xi \in {\mathfrak q}^{*}$
, the stabilizer
![]() ${\mathfrak q}^{\xi }$
is generic (i.e.,
${\mathfrak q}^{\xi }$
is generic (i.e.,
![]() $\xi $
is a Q-generic point) if and only if
$\xi $
is a Q-generic point) if and only if
The reason is that
![]() $({\mathfrak q}{\cdot }\xi )^{\perp }={\mathfrak q}^{\xi }$
and
$({\mathfrak q}{\cdot }\xi )^{\perp }={\mathfrak q}^{\xi }$
and
![]() $(({\mathfrak q}^{*})^{{\mathfrak q}_{\xi }})^{\perp }=[{\mathfrak q},{\mathfrak q}^{\xi }]$
, where
$(({\mathfrak q}^{*})^{{\mathfrak q}_{\xi }})^{\perp }=[{\mathfrak q},{\mathfrak q}^{\xi }]$
, where
![]() $(\cdot )^{\perp }$
stands for the annihilator in the dual space.
$(\cdot )^{\perp }$
stands for the annihilator in the dual space.
3.2 The Frobenius semiradical
For the Q-module
![]() ${\mathbb {V}}={\mathfrak q}^{*}$
, the set of Q-regular (or just “regular”) points
${\mathbb {V}}={\mathfrak q}^{*}$
, the set of Q-regular (or just “regular”) points
![]() ${\mathfrak q}^{*}_{\mathsf {reg}}$
consists of all
${\mathfrak q}^{*}_{\mathsf {reg}}$
consists of all
![]() $\xi \in {\mathfrak q}^{*}$
such that the stabilizer
$\xi \in {\mathfrak q}^{*}$
such that the stabilizer
![]() ${\mathfrak q}^{\xi }$
has the minimal possible dimension. If
${\mathfrak q}^{\xi }$
has the minimal possible dimension. If
![]() $\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
, then
$\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
, then
![]() ${\mathrm {ind}}\,{\mathfrak q}:=\dim {\mathfrak q}^{\xi }$
is the index of (a Lie algebra)
${\mathrm {ind}}\,{\mathfrak q}:=\dim {\mathfrak q}^{\xi }$
is the index of (a Lie algebra)
![]() ${\mathfrak q}$
. The Frobenius semiradical
${\mathfrak q}$
. The Frobenius semiradical
![]() ${\mathcal F}({\mathfrak q})$
of a Lie algebra
${\mathcal F}({\mathfrak q})$
of a Lie algebra
![]() ${\mathfrak q}$
is introduced by Ooms (see [Reference Ooms18, Reference Ooms19]). By definition,
${\mathfrak q}$
is introduced by Ooms (see [Reference Ooms18, Reference Ooms19]). By definition,
Obviously,
![]() ${\mathcal F}({\mathfrak q})$
is a characteristic ideal of
${\mathcal F}({\mathfrak q})$
is a characteristic ideal of
![]() ${\mathfrak q}$
, and
${\mathfrak q}$
, and
![]() ${\mathcal F}({\mathfrak q})=0$
if and only
${\mathcal F}({\mathfrak q})=0$
if and only
![]() ${\mathrm {ind}}\,{\mathfrak q}=0$
(i.e.,
${\mathrm {ind}}\,{\mathfrak q}=0$
(i.e.,
![]() ${\mathfrak q}$
is a Frobenius Lie algebra). Note that if
${\mathfrak q}$
is a Frobenius Lie algebra). Note that if
![]() $({\mathfrak q}:{\mathfrak q}^{*})$
has a generic stabilizer, then any Q-generic point in the sense of Section 3.1 is regular, but not vice versa.
$({\mathfrak q}:{\mathfrak q}^{*})$
has a generic stabilizer, then any Q-generic point in the sense of Section 3.1 is regular, but not vice versa.
Lemma 3.1 (cf. [Reference Ooms19, Proposition 1.7])
If
![]() $({\mathfrak q}:{\mathfrak q}^{*})$
has a generic stabilizer and
$({\mathfrak q}:{\mathfrak q}^{*})$
has a generic stabilizer and
![]() $\xi \in {\mathfrak q}^{*}$
is any generic point, then
$\xi \in {\mathfrak q}^{*}$
is any generic point, then
![]() ${\mathcal F}({\mathfrak q})$
is the
${\mathcal F}({\mathfrak q})$
is the
![]() ${\mathfrak q}$
-ideal generated by the sole stabilizer
${\mathfrak q}$
-ideal generated by the sole stabilizer
![]() ${\mathfrak q}^{\xi }$
.
${\mathfrak q}^{\xi }$
.
Proof By [Reference Ooms19, Lemma 1.2], if
![]() $\Psi $
is open and dense in
$\Psi $
is open and dense in
![]() ${\mathfrak q}^{*}_{\mathsf {reg}}$
, then
${\mathfrak q}^{*}_{\mathsf {reg}}$
, then
![]() ${\mathcal F}({\mathfrak q})=\sum _{\eta \in \Psi }{\mathfrak q}^{\eta }$
. Applying this to the set of generic points
${\mathcal F}({\mathfrak q})=\sum _{\eta \in \Psi }{\mathfrak q}^{\eta }$
. Applying this to the set of generic points
![]() $\Omega \subset {\mathfrak q}^{*}_{\mathsf {reg}}$
, we obtain
$\Omega \subset {\mathfrak q}^{*}_{\mathsf {reg}}$
, we obtain
![]() ${\mathcal F}({\mathfrak q})=\sum _{\eta \in \Omega }{\mathfrak q}^{\eta }=\sum _{g\in Q}{\mathfrak q}^{g{\cdot }\xi }$
. Clearly, the last sum yields the ideal of
${\mathcal F}({\mathfrak q})=\sum _{\eta \in \Omega }{\mathfrak q}^{\eta }=\sum _{g\in Q}{\mathfrak q}^{g{\cdot }\xi }$
. Clearly, the last sum yields the ideal of
![]() ${\mathfrak q}$
generated by
${\mathfrak q}$
generated by
![]() ${\mathfrak q}^{\xi }$
.
${\mathfrak q}^{\xi }$
.
If
![]() ${\mathfrak q}$
is quadratic, i.e.,
${\mathfrak q}$
is quadratic, i.e.,
![]() ${\mathfrak q}\simeq {\mathfrak q}^{*}$
as Q-module, then
${\mathfrak q}\simeq {\mathfrak q}^{*}$
as Q-module, then
![]() ${\mathcal F}({\mathfrak q})=\sum _{x\in {\mathfrak q}_{\mathsf {reg}}}{\mathfrak q}^x$
. Since
${\mathcal F}({\mathfrak q})=\sum _{x\in {\mathfrak q}_{\mathsf {reg}}}{\mathfrak q}^x$
. Since
![]() $x\in {\mathfrak q}^x$
for any
$x\in {\mathfrak q}^x$
for any
![]() $x\in {\mathfrak q}$
, we see that here
$x\in {\mathfrak q}$
, we see that here
![]() ${\mathcal F}({\mathfrak q})={\mathfrak q}$
(cf. [Reference Elashvili and Ooms10, Theorem 3.2]). In particular, this is the case if
${\mathcal F}({\mathfrak q})={\mathfrak q}$
(cf. [Reference Elashvili and Ooms10, Theorem 3.2]). In particular, this is the case if
![]() ${\mathfrak q}$
is reductive. Following Ooms,
${\mathfrak q}$
is reductive. Following Ooms,
![]() ${\mathfrak q}$
is said to be quasi-quadratic if
${\mathfrak q}$
is said to be quasi-quadratic if
![]() ${\mathcal F}({\mathfrak q})={\mathfrak q}$
. Another interesting property of the functor
${\mathcal F}({\mathfrak q})={\mathfrak q}$
. Another interesting property of the functor
![]() ${\mathcal F}(\cdot )$
is that
${\mathcal F}(\cdot )$
is that
![]() ${\mathrm {ind}}\,{\mathfrak q}\leqslant {\mathrm {ind}}\,{\mathcal F}({\mathfrak q})$
and
${\mathrm {ind}}\,{\mathfrak q}\leqslant {\mathrm {ind}}\,{\mathcal F}({\mathfrak q})$
and
![]() ${\mathcal F}({\mathcal F}({\mathfrak q}))={\mathcal F}({\mathfrak q})$
[Reference Ooms19].
${\mathcal F}({\mathcal F}({\mathfrak q}))={\mathcal F}({\mathfrak q})$
[Reference Ooms19].
3.3 Commutative polarizations
If
![]() ${\mathfrak a}$
is an abelian subalgebra of
${\mathfrak a}$
is an abelian subalgebra of
![]() ${\mathfrak q}$
, then
${\mathfrak q}$
, then
![]() $\dim {\mathfrak a}\leqslant \boldsymbol {b}({\mathfrak q})$
(see [Reference Vinberg28, 0.2] or [Reference Ooms18, Theorem 14]). If
$\dim {\mathfrak a}\leqslant \boldsymbol {b}({\mathfrak q})$
(see [Reference Vinberg28, 0.2] or [Reference Ooms18, Theorem 14]). If
![]() $\dim {\mathfrak a}= \boldsymbol {b}({\mathfrak q})$
, then
$\dim {\mathfrak a}= \boldsymbol {b}({\mathfrak q})$
, then
![]() ${\mathfrak a}$
is called a commutative polarization (=CP) of
${\mathfrak a}$
is called a commutative polarization (=CP) of
![]() ${\mathfrak q}$
, and we say that
${\mathfrak q}$
, and we say that
![]() ${\mathfrak q}$
has a CP. If
${\mathfrak q}$
has a CP. If
![]() ${\mathfrak a}$
is a CP and also an ideal of
${\mathfrak a}$
is a CP and also an ideal of
![]() ${\mathfrak q}$
, then it is called a CP-ideal. If
${\mathfrak q}$
, then it is called a CP-ideal. If
![]() ${\mathfrak q}$
is solvable and has a CP, then it also has a CP-ideal (see [Reference Elashvili and Ooms10, Theorem 4.1]). More generally, a similar argument shows that if
${\mathfrak q}$
is solvable and has a CP, then it also has a CP-ideal (see [Reference Elashvili and Ooms10, Theorem 4.1]). More generally, a similar argument shows that if
![]() ${\mathfrak q}$
is an ideal of a solvable Lie algebra
${\mathfrak q}$
is an ideal of a solvable Lie algebra
![]() ${\mathfrak r}$
and
${\mathfrak r}$
and
![]() ${\mathfrak q}$
has a CP, then
${\mathfrak q}$
has a CP, then
![]() ${\mathfrak q}$
has a CP-ideal that is
${\mathfrak q}$
has a CP-ideal that is
![]() ${\mathfrak r}$
-stable. A standard nilradical
${\mathfrak r}$
-stable. A standard nilradical
![]() ${\mathfrak n}$
is an ideal of
${\mathfrak n}$
is an ideal of
![]() ${\mathfrak b}$
. Therefore, if
${\mathfrak b}$
. Therefore, if
![]() ${\mathfrak n}$
has a CP, then it also has a CP-ideal that is
${\mathfrak n}$
has a CP, then it also has a CP-ideal that is
![]() ${\mathfrak b}$
-stable. Henceforth, “a CP-ideal of
${\mathfrak b}$
-stable. Henceforth, “a CP-ideal of
![]() ${\mathfrak n}$
” means “a
${\mathfrak n}$
” means “a
![]() ${\mathfrak b}$
-stable CP-ideal of
${\mathfrak b}$
-stable CP-ideal of
![]() ${\mathfrak n}$
.”
${\mathfrak n}$
.”
Basic results on commutative polarizations are presented in [Reference Elashvili and Ooms10]. It is also shown therein that if
![]() ${\mathfrak g}$
is of type
${\mathfrak g}$
is of type
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
or
${\mathsf {\mathbf {{A}}}}_{n}$
or
![]() ${\mathsf {\mathbf {{C}}}}_{n}$
, then every nilradical in
${\mathsf {\mathbf {{C}}}}_{n}$
, then every nilradical in
![]() ${\mathfrak g}$
has a CP. A complete classification of the nilradicals having a CP is obtained in [Reference Panyushev22]. By Lemma 2.1,
${\mathfrak g}$
has a CP. A complete classification of the nilradicals having a CP is obtained in [Reference Panyushev22]. By Lemma 2.1, ![]() is abelian if and only if
is abelian if and only if ![]() and
and
![]() $[\theta :\alpha ]=1$
. The abelian nilradical
$[\theta :\alpha ]=1$
. The abelian nilradical
![]() ${\mathfrak n}_{\{\alpha \}}$
play a key role in our theory. By Theorems 3.10 and 4.1 in [Reference Panyushev22], a nilradical
${\mathfrak n}_{\{\alpha \}}$
play a key role in our theory. By Theorems 3.10 and 4.1 in [Reference Panyushev22], a nilradical
![]() ${\mathfrak n}$
has a CP if and only if at least one of the following two conditions is satisfied:
${\mathfrak n}$
has a CP if and only if at least one of the following two conditions is satisfied:
-
(1)
 ${\mathfrak n}={\mathfrak n}_{\theta }={\mathfrak h}_1$
is the Heisenberg nilradical. In this case, if
${\mathfrak n}={\mathfrak n}_{\theta }={\mathfrak h}_1$
is the Heisenberg nilradical. In this case, if
 ${\mathfrak a}$
is any maximal abelian ideal of
${\mathfrak a}$
is any maximal abelian ideal of
 ${\mathfrak b}$
, then
${\mathfrak b}$
, then
 ${\mathfrak a}\cap {\mathfrak n}$
is a CP-ideal of
${\mathfrak a}\cap {\mathfrak n}$
is a CP-ideal of
 ${\mathfrak n}$
, and vice versa.
${\mathfrak n}$
, and vice versa. -
(2) There is an abelian nilradical
 ${\mathfrak n}_{\{\alpha \}}$
such that
${\mathfrak n}_{\{\alpha \}}$
such that
 ${\mathfrak n}$
is contained in
${\mathfrak n}$
is contained in
 $\widetilde {{\mathfrak n}_{\{\alpha \}}}$
, the optimization of
$\widetilde {{\mathfrak n}_{\{\alpha \}}}$
, the optimization of
 ${\mathfrak n}_{\{\alpha \}}$
. (There can be several abelian nilradicals with this property, and, for a “right” choice of such
${\mathfrak n}_{\{\alpha \}}$
. (There can be several abelian nilradicals with this property, and, for a “right” choice of such
 $\check \alpha \in \Pi $
,
$\check \alpha \in \Pi $
,
 ${\mathfrak n}\cap {\mathfrak n}_{\{\check \alpha \}}$
is a CP-ideal of
${\mathfrak n}\cap {\mathfrak n}_{\{\check \alpha \}}$
is a CP-ideal of
 ${\mathfrak n}$
(cf. also Section 8)).
${\mathfrak n}$
(cf. also Section 8)).
If
![]() ${\mathfrak g}$
has no parabolic subalgebras with abelian nilradicals, then the Heisenberg nilradical
${\mathfrak g}$
has no parabolic subalgebras with abelian nilradicals, then the Heisenberg nilradical
![]() ${\mathfrak n}_{\theta }={\mathfrak h}_1$
is the only nilradical with CP. This happens precisely if
${\mathfrak n}_{\theta }={\mathfrak h}_1$
is the only nilradical with CP. This happens precisely if
![]() ${\mathfrak g}$
is of type
${\mathfrak g}$
is of type
![]() ${\mathsf {\mathbf {{G}}}}_{2}$
,
${\mathsf {\mathbf {{G}}}}_{2}$
,
![]() ${\mathsf {\mathbf {{F}}}}_{4}$
,
${\mathsf {\mathbf {{F}}}}_{4}$
,
![]() ${\mathsf {\mathbf {{E}}}}_{8}$
. Another result of [Reference Panyushev22] is that
${\mathsf {\mathbf {{E}}}}_{8}$
. Another result of [Reference Panyushev22] is that
![]() ${\mathfrak n}$
has a CP if and only if
${\mathfrak n}$
has a CP if and only if
![]() $\tilde {\mathfrak n}$
has.
$\tilde {\mathfrak n}$
has.
3.4 The role of commutative polarizations
If
![]() ${\mathfrak a}$
is a CP of a Lie algebra
${\mathfrak a}$
is a CP of a Lie algebra
![]() ${\mathfrak q}$
, then:
${\mathfrak q}$
, then:
-
(1)
 ${\mathcal F}({\mathfrak q})\subset {\mathfrak a}$
[Reference Ooms18, Proposition 20] and thereby
${\mathcal F}({\mathfrak q})\subset {\mathfrak a}$
[Reference Ooms18, Proposition 20] and thereby
 ${\mathcal F}({\mathfrak q})$
is an abelian ideal. (However, it can happen that
${\mathcal F}({\mathfrak q})$
is an abelian ideal. (However, it can happen that
 ${\mathcal F}({\mathfrak q})$
is abelian, whereas
${\mathcal F}({\mathfrak q})$
is abelian, whereas
 ${\mathfrak q}$
has no CP (see Example 7.3).)
${\mathfrak q}$
has no CP (see Example 7.3).) -
(2) Since
 ${\mathfrak a}$
is abelian,
${\mathfrak a}$
is abelian,
 $\boldsymbol {b}({\mathfrak a})=\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
. Therefore, the Poisson center
$\boldsymbol {b}({\mathfrak a})=\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
. Therefore, the Poisson center  is contained in
is contained in  [Reference Panyushev22, Proposition 5.5]. Hence, if
[Reference Panyushev22, Proposition 5.5]. Hence, if
 ${\mathfrak a}$
is a CP-ideal of
${\mathfrak a}$
is a CP-ideal of
 ${\mathfrak q}$
, then
${\mathfrak q}$
, then  .
. -
(3) Thus, if
 ${\mathfrak a}_1,\dots ,{\mathfrak a}_s$
are different CP in
${\mathfrak a}_1,\dots ,{\mathfrak a}_s$
are different CP in
 ${\mathfrak q}$
, then
${\mathfrak q}$
, then
 ${\mathcal F}({\mathfrak q})\subset \bigcap _{i=1}^s {\mathfrak a}_i$
and
${\mathcal F}({\mathfrak q})\subset \bigcap _{i=1}^s {\mathfrak a}_i$
and  .
.
In many cases, the presence of a CP in
![]() ${\mathfrak n}$
allows us to quickly describe the Frobenius semiradical for
${\mathfrak n}$
allows us to quickly describe the Frobenius semiradical for
![]() ${\mathfrak n}$
(see Sections 5.1 and 5.2). For the reader’s convenience, we provide an invariant-theoretic proof for two basic results on abelian subalgebras mentioned above.
${\mathfrak n}$
(see Sections 5.1 and 5.2). For the reader’s convenience, we provide an invariant-theoretic proof for two basic results on abelian subalgebras mentioned above.
Proposition 3.2 Let
![]() ${\mathfrak a}$
be an abelian subalgebra of
${\mathfrak a}$
be an abelian subalgebra of
![]() ${\mathfrak q}$
. Then:
${\mathfrak q}$
. Then:
-
(1)
 $\dim {\mathfrak a}\leqslant \boldsymbol {b}({\mathfrak q})$
.
$\dim {\mathfrak a}\leqslant \boldsymbol {b}({\mathfrak q})$
. -
(2) If
 $\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
, then
$\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
, then
 ${\mathfrak q}^{\xi }\subset {\mathfrak a}$
for any
${\mathfrak q}^{\xi }\subset {\mathfrak a}$
for any
 $\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
, i.e.,
$\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
, i.e.,
 ${\mathcal F}({\mathfrak q})\subset {\mathfrak a}$
.
${\mathcal F}({\mathfrak q})\subset {\mathfrak a}$
.
Proof We show that both assertions are immediate consequences of Rosenlicht’s theorem [Reference Brion4, Chapter 1.6]. Let
![]() $A\subset Q$
be the connected (abelian) subgroup with
$A\subset Q$
be the connected (abelian) subgroup with
![]() ${{\mathrm {Lie\,}} A={\mathfrak a}}$
. For the A-action on
${{\mathrm {Lie\,}} A={\mathfrak a}}$
. For the A-action on
![]() ${\mathfrak q}^{*}$
, let
${\mathfrak q}^{*}$
, let
![]() ${\mathbb C}({\mathfrak q}^{*})^A$
denote the field of A-invariant rational functions on
${\mathbb C}({\mathfrak q}^{*})^A$
denote the field of A-invariant rational functions on
![]() ${\mathfrak q}^{*}$
.
${\mathfrak q}^{*}$
.
(1) Since
![]() ${\mathfrak a}$
is abelian, we have
${\mathfrak a}$
is abelian, we have ![]() ; hence,
; hence,
![]() ${\mathrm {trdeg\,}}{\mathbb C}({\mathfrak q}^{*})^A\geqslant \dim {\mathfrak a}$
. By Rosenlicht’s theorem,
${\mathrm {trdeg\,}}{\mathbb C}({\mathfrak q}^{*})^A\geqslant \dim {\mathfrak a}$
. By Rosenlicht’s theorem,
Therefore,
(2) If
![]() $\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
, then
$\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
, then
![]() $\min _{\xi \in {\mathfrak q}^{*}}\dim {\mathfrak a}^{\xi }={\mathrm {ind}}\,{\mathfrak q}$
. For
$\min _{\xi \in {\mathfrak q}^{*}}\dim {\mathfrak a}^{\xi }={\mathrm {ind}}\,{\mathfrak q}$
. For
![]() $\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
, one has
$\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
, one has
![]() $\dim {\mathfrak q}^{\xi }={\mathrm {ind}}\,{\mathfrak q}$
. That is,
$\dim {\mathfrak q}^{\xi }={\mathrm {ind}}\,{\mathfrak q}$
. That is,
![]() ${\mathfrak a}^{\xi }={\mathfrak q}^{\xi }\subset {\mathfrak a}$
for any
${\mathfrak a}^{\xi }={\mathfrak q}^{\xi }\subset {\mathfrak a}$
for any
![]() $\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
.
$\xi \in {\mathfrak q}^{*}_{\mathsf {reg}}$
.
The proof above also implies that if
![]() $\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
, then
$\dim {\mathfrak a}=\boldsymbol {b}({\mathfrak q})$
, then
![]() ${\mathrm {trdeg\,}}{\mathbb C}({\mathfrak q}^{*})^A=\dim {\mathfrak a}$
. Therefore,
${\mathrm {trdeg\,}}{\mathbb C}({\mathfrak q}^{*})^A=\dim {\mathfrak a}$
. Therefore, ![]() and
and
![]() ${\mathbb C}({\mathfrak q}^{*})^A$
is the fraction field of
${\mathbb C}({\mathfrak q}^{*})^A$
is the fraction field of ![]() .
.
4 Generic stabilizers and the Frobenius semiradical for the nilradicals
In this section, we study the Frobenius semiradical,
![]() ${\mathcal F}({\mathfrak n})$
, of a nilradical
${\mathcal F}({\mathfrak n})$
, of a nilradical
![]() ${\mathfrak n}\subset {\mathfrak g}$
and the existence of generic stabilizers for the coadjoint representation of
${\mathfrak n}\subset {\mathfrak g}$
and the existence of generic stabilizers for the coadjoint representation of
![]() $N=\exp ({\mathfrak n})$
. We also say that “
$N=\exp ({\mathfrak n})$
. We also say that “
![]() ${\mathfrak n}$
has a generic stabilizer,” if the coadjoint representation
${\mathfrak n}$
has a generic stabilizer,” if the coadjoint representation
![]() $(N:{\mathfrak n}^{*})$
has.
$(N:{\mathfrak n}^{*})$
has.
Let
![]() ${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
be a standard nilradical and
${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
be a standard nilradical and
![]() ${\mathfrak n}^-=({\mathfrak p}^-)^{\mathsf {nil}}$
the opposite nilradical, i.e.,
${\mathfrak n}^-=({\mathfrak p}^-)^{\mathsf {nil}}$
the opposite nilradical, i.e.,
![]() $\Delta ({\mathfrak n}^-)=-\Delta ({\mathfrak n})$
. Using the vector space sum
$\Delta ({\mathfrak n}^-)=-\Delta ({\mathfrak n})$
. Using the vector space sum
![]() ${\mathfrak g}={\mathfrak p}\oplus {\mathfrak n}^-$
and the P-module isomorphism
${\mathfrak g}={\mathfrak p}\oplus {\mathfrak n}^-$
and the P-module isomorphism
![]() ${\mathfrak n}^{*}\simeq {\mathfrak g}/{\mathfrak p}$
, we identify
${\mathfrak n}^{*}\simeq {\mathfrak g}/{\mathfrak p}$
, we identify
![]() ${\mathfrak n}^{*}$
with
${\mathfrak n}^{*}$
with
![]() ${\mathfrak n}^-$
and thereby regard
${\mathfrak n}^-$
and thereby regard
![]() ${\mathfrak n}^-$
as P-module. In terms of
${\mathfrak n}^-$
as P-module. In terms of
![]() ${\mathfrak n}^-$
, the
${\mathfrak n}^-$
, the
![]() ${\mathfrak p}$
-action on
${\mathfrak p}$
-action on
![]() ${\mathfrak n}^{*}$
is given by the Lie bracket in
${\mathfrak n}^{*}$
is given by the Lie bracket in
![]() ${\mathfrak g}$
, with the subsequent projection to
${\mathfrak g}$
, with the subsequent projection to
![]() ${\mathfrak n}^-$
. In particular, the coadjoint representation
${\mathfrak n}^-$
. In particular, the coadjoint representation
![]() $ {\mathrm {ad}}^{*} _{\mathfrak n}$
of
$ {\mathrm {ad}}^{*} _{\mathfrak n}$
of
![]() ${\mathfrak n}$
has the following interpretation. If
${\mathfrak n}$
has the following interpretation. If
![]() $x\in {\mathfrak n}$
and
$x\in {\mathfrak n}$
and
![]() $\xi \in {\mathfrak n}^-$
, then
$\xi \in {\mathfrak n}^-$
, then
![]() $( {\mathrm {ad}}^{*} _{\mathfrak n} x){\cdot }\xi =\mathsf {pr}_{{\mathfrak n}^-} ([x,\xi ])$
, where
$( {\mathrm {ad}}^{*} _{\mathfrak n} x){\cdot }\xi =\mathsf {pr}_{{\mathfrak n}^-} ([x,\xi ])$
, where
![]() $\mathsf {pr}_{{\mathfrak n}^-}: {\mathfrak g}\to {\mathfrak n}^-$
is the projection with kernel
$\mathsf {pr}_{{\mathfrak n}^-}: {\mathfrak g}\to {\mathfrak n}^-$
is the projection with kernel
![]() ${\mathfrak p}$
.
${\mathfrak p}$
.
Recall that ![]() . Set
. Set ![]() and
and ![]() . We say that
. We say that
![]() ${\mathfrak k}$
is a cascade subspace of
${\mathfrak k}$
is a cascade subspace of
![]() ${\mathfrak n}^{*}$
and
${\mathfrak n}^{*}$
and
![]() ${\boldsymbol {\zeta }}$
is a cascade point of
${\boldsymbol {\zeta }}$
is a cascade point of
![]() ${\mathfrak n}^{*}$
. Clearly,
${\mathfrak n}^{*}$
. Clearly,
![]() ${\boldsymbol {\zeta }}$
depends on the choice of nonzero root vectors
${\boldsymbol {\zeta }}$
depends on the choice of nonzero root vectors
![]() $e_{-\beta }\in {\mathfrak g}_{-\beta }$
, but all such points
$e_{-\beta }\in {\mathfrak g}_{-\beta }$
, but all such points
![]() ${\boldsymbol {\zeta }}$
form a sole dense T-orbit in
${\boldsymbol {\zeta }}$
form a sole dense T-orbit in
![]() ${\mathfrak k}$
, which is denoted by
${\mathfrak k}$
, which is denoted by
![]() ${\mathfrak k}_0$
. That is,
${\mathfrak k}_0$
. That is, ![]() . It was proved by Joseph [Reference Joseph12, 2.4] that upon the identification of
. It was proved by Joseph [Reference Joseph12, 2.4] that upon the identification of
![]() ${\mathfrak n}^-$
and
${\mathfrak n}^-$
and
![]() ${\mathfrak n}^{*}$
as P-modules and hence B-modules,
${\mathfrak n}^{*}$
as P-modules and hence B-modules,
![]() $B{\cdot }{\boldsymbol {\zeta }}$
is dense in
$B{\cdot }{\boldsymbol {\zeta }}$
is dense in
![]() ${\mathfrak n}^{*}$
and
${\mathfrak n}^{*}$
and
![]() $B{\cdot }{\boldsymbol {\zeta }}\subset {\mathfrak n}^{*}_{\mathsf {reg}}$
. In particular,
$B{\cdot }{\boldsymbol {\zeta }}\subset {\mathfrak n}^{*}_{\mathsf {reg}}$
. In particular,
![]() ${\mathfrak k}_0\subset {\mathfrak n}^{*}_{\mathsf {reg}}$
.
${\mathfrak k}_0\subset {\mathfrak n}^{*}_{\mathsf {reg}}$
.
Proposition 4.1 Let
![]() ${\mathfrak n}$
be an arbitrary nilradical and
${\mathfrak n}$
be an arbitrary nilradical and
![]() ${\boldsymbol {\zeta }}\in {\mathfrak n}^{*}$
a cascade point. Then:
${\boldsymbol {\zeta }}\in {\mathfrak n}^{*}$
a cascade point. Then:
-
(i)
 ${\mathcal F}({\mathfrak n})$
is the
${\mathcal F}({\mathfrak n})$
is the
 ${\mathfrak b}$
-stable ideal of
${\mathfrak b}$
-stable ideal of
 ${\mathfrak n}$
generated by
${\mathfrak n}$
generated by
 ${\mathfrak n}^{\boldsymbol {\zeta }}$
.
${\mathfrak n}^{\boldsymbol {\zeta }}$
. -
(ii)
 $({\mathfrak n}:{\mathfrak n}^{*})$
has a generic stabilizer if and only if the stabilizer
$({\mathfrak n}:{\mathfrak n}^{*})$
has a generic stabilizer if and only if the stabilizer
 ${\mathfrak n}^{\boldsymbol {\zeta }}$
is generic.
${\mathfrak n}^{\boldsymbol {\zeta }}$
is generic.
Proof
(i) Since
![]() $B{\cdot }{\boldsymbol {\zeta }}$
is dense in
$B{\cdot }{\boldsymbol {\zeta }}$
is dense in
![]() ${\mathfrak n}^{*}_{\mathsf {reg}}$
, a result of Ooms [Reference Ooms19, Lemma 1.2] implies that
${\mathfrak n}^{*}_{\mathsf {reg}}$
, a result of Ooms [Reference Ooms19, Lemma 1.2] implies that
![]() ${\mathcal F}({\mathfrak n})=\sum _{b\in B}{\mathfrak n}^{b{\cdot }{\boldsymbol {\zeta }}}$
. Clearly, the last sum is the smallest
${\mathcal F}({\mathfrak n})=\sum _{b\in B}{\mathfrak n}^{b{\cdot }{\boldsymbol {\zeta }}}$
. Clearly, the last sum is the smallest
![]() ${\mathfrak b}$
-stable ideal containing
${\mathfrak b}$
-stable ideal containing
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
.
${\mathfrak n}^{\boldsymbol {\zeta }}$
.
(ii) If
![]() ${\boldsymbol {\zeta }}$
is not generic, then
${\boldsymbol {\zeta }}$
is not generic, then
![]() $[{\mathfrak n},{\mathfrak n}^{{\boldsymbol {\zeta }}}]\cap {\mathfrak n}^{{\boldsymbol {\zeta }}} \ne \{0\}$
and hence
$[{\mathfrak n},{\mathfrak n}^{{\boldsymbol {\zeta }}}]\cap {\mathfrak n}^{{\boldsymbol {\zeta }}} \ne \{0\}$
and hence
![]() $[{\mathfrak n},{\mathfrak n}^{b{\cdot }{\boldsymbol {\zeta }}}]\cap {\mathfrak n}^{b{\cdot }{\boldsymbol {\zeta }}} \ne \{0\}$
for any
$[{\mathfrak n},{\mathfrak n}^{b{\cdot }{\boldsymbol {\zeta }}}]\cap {\mathfrak n}^{b{\cdot }{\boldsymbol {\zeta }}} \ne \{0\}$
for any
![]() $b\in B$
. Therefore, neither of the points
$b\in B$
. Therefore, neither of the points
![]() ${b{\cdot }{\boldsymbol {\zeta }}}$
(
${b{\cdot }{\boldsymbol {\zeta }}}$
(
![]() $b\in B$
) can be generic. Since
$b\in B$
) can be generic. Since
![]() $B{\cdot }{\boldsymbol {\zeta }}$
is dense in
$B{\cdot }{\boldsymbol {\zeta }}$
is dense in
![]() ${\mathfrak n}^{*}$
, this means that generic points cannot exist in such a case.
${\mathfrak n}^{*}$
, this means that generic points cannot exist in such a case.
The point of Proposition 4.1
(i) is that the existence of a generic stabilizer for
![]() ${\mathfrak n}$
is not required (cf. Lemma 3.1). We use instead the action of B on
${\mathfrak n}$
is not required (cf. Lemma 3.1). We use instead the action of B on
![]() ${\mathfrak n}^{*}$
.
${\mathfrak n}^{*}$
.
Proposition 4.2 If
![]() ${\mathfrak n}$
is an optimal nilradical, then:
${\mathfrak n}$
is an optimal nilradical, then:
-
(i)
 ${\mathfrak n}^{\boldsymbol {\zeta }}$
is a generic stabilizer for
${\mathfrak n}^{\boldsymbol {\zeta }}$
is a generic stabilizer for
 $({\mathfrak n}:{\mathfrak n}^{*})$
.
$({\mathfrak n}:{\mathfrak n}^{*})$
. -
(ii) The N-saturation of
 ${\mathfrak k}$
is dense in
${\mathfrak k}$
is dense in
 ${\mathfrak n}^{*}$
, i.e.,
${\mathfrak n}^{*}$
, i.e.,
 $\overline {N{\cdot }{\mathfrak k}}={\mathfrak n}^{*}$
.
$\overline {N{\cdot }{\mathfrak k}}={\mathfrak n}^{*}$
.
Proof
(i) For an optimal nilradical
![]() ${\mathfrak n}$
, one has
${\mathfrak n}$
, one has ![]() [Reference Joseph12, 2.4]. Since the roots in
[Reference Joseph12, 2.4]. Since the roots in ![]() are strongly orthogonal, condition (3.3) is satisfied for
are strongly orthogonal, condition (3.3) is satisfied for
![]() $\xi ={\boldsymbol {\zeta }}$
.
$\xi ={\boldsymbol {\zeta }}$
.
(ii) Recall that ![]() and
and
![]() ${\mathrm {codim\,}}_{{\mathfrak n}^{*}}({\mathfrak n}{\cdot }\xi )={\mathrm {ind}}\,{\mathfrak n}$
for any
${\mathrm {codim\,}}_{{\mathfrak n}^{*}}({\mathfrak n}{\cdot }\xi )={\mathrm {ind}}\,{\mathfrak n}$
for any
![]() $\xi \in {\mathfrak k}_0$
. Furthermore,
$\xi \in {\mathfrak k}_0$
. Furthermore,
![]() ${\mathfrak n}{\cdot }\xi \cap {\mathfrak k}=\{0\}$
for any
${\mathfrak n}{\cdot }\xi \cap {\mathfrak k}=\{0\}$
for any
![]() $\xi \in {\mathfrak k}$
. (Use again the strong orthogonality.) Hence,
$\xi \in {\mathfrak k}$
. (Use again the strong orthogonality.) Hence,
![]() ${\mathfrak n}{\cdot }\xi \oplus {\mathfrak k}={\mathfrak n}^{*}$
for any
${\mathfrak n}{\cdot }\xi \oplus {\mathfrak k}={\mathfrak n}^{*}$
for any
![]() $\xi \in {\mathfrak k}_0$
, which implies that
$\xi \in {\mathfrak k}_0$
, which implies that
![]() $N{\cdot }{\mathfrak k}_0$
is open and dense in
$N{\cdot }{\mathfrak k}_0$
is open and dense in
![]() ${\mathfrak n}^{*}$
(cf. [Reference Elashvili8, Lemma 1.1]).
${\mathfrak n}^{*}$
(cf. [Reference Elashvili8, Lemma 1.1]).
Recall that
![]() $\tilde {\mathfrak n}$
denotes the optimization of
$\tilde {\mathfrak n}$
denotes the optimization of
![]() ${\mathfrak n}$
. Then
${\mathfrak n}$
. Then ![]() ,
, ![]() , and
, and
The cascade subspaces and cascade points associated with
![]() ${\mathfrak n}$
or
${\mathfrak n}$
or
![]() $\tilde {\mathfrak n}$
are the same, if regarded as objects in
$\tilde {\mathfrak n}$
are the same, if regarded as objects in
![]() ${\mathfrak u}^-$
. But one has to distinguish them as objects in
${\mathfrak u}^-$
. But one has to distinguish them as objects in
![]() ${\mathfrak n}^{*}$
or
${\mathfrak n}^{*}$
or
![]() $\tilde {\mathfrak n}^{*}$
. For this reason, working simultaneously with
$\tilde {\mathfrak n}^{*}$
. For this reason, working simultaneously with
![]() ${\mathfrak n}$
and
${\mathfrak n}$
and
![]() $\tilde {\mathfrak n}$
, we write
$\tilde {\mathfrak n}$
, we write
![]() $\tilde {\boldsymbol {\zeta }}$
for a cascade point in the cascade subspace
$\tilde {\boldsymbol {\zeta }}$
for a cascade point in the cascade subspace
![]() $\tilde {\mathfrak k}\subset \tilde {\mathfrak n}^{*}$
. Note that, for the natural projection
$\tilde {\mathfrak k}\subset \tilde {\mathfrak n}^{*}$
. Note that, for the natural projection
![]() $\tau : \tilde {\mathfrak n}^{*}\to {\mathfrak n}^{*}$
, one has
$\tau : \tilde {\mathfrak n}^{*}\to {\mathfrak n}^{*}$
, one has
![]() $\tau (\tilde {\mathfrak k})={\mathfrak k}$
and
$\tau (\tilde {\mathfrak k})={\mathfrak k}$
and
![]() $\tau (\tilde {\boldsymbol {\zeta }})={\boldsymbol {\zeta }}$
. Since
$\tau (\tilde {\boldsymbol {\zeta }})={\boldsymbol {\zeta }}$
. Since
![]() $\tau $
is B-equivariant, this allows us to transfer some good properties from the coadjoint action
$\tau $
is B-equivariant, this allows us to transfer some good properties from the coadjoint action
![]() $(\tilde N:\tilde {\mathfrak n}^{*})$
to the coadjoint action
$(\tilde N:\tilde {\mathfrak n}^{*})$
to the coadjoint action
![]() $(N: {\mathfrak n}^{*})$
.
$(N: {\mathfrak n}^{*})$
.
If
![]() ${\mathfrak n}$
is not optimal, then it may or may not have a generic stabilizer. To see this, we provide an explicit description of
${\mathfrak n}$
is not optimal, then it may or may not have a generic stabilizer. To see this, we provide an explicit description of
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
for an arbitrary nilradical
${\mathfrak n}^{\boldsymbol {\zeta }}$
for an arbitrary nilradical
![]() ${\mathfrak n}$
, which generalizes Joseph’s description for the optimal nilradicals.
${\mathfrak n}$
, which generalizes Joseph’s description for the optimal nilradicals.
Because
![]() ${\boldsymbol {\zeta }}\in {\mathfrak n}^{*}_{\mathsf {reg}}$
and
${\boldsymbol {\zeta }}\in {\mathfrak n}^{*}_{\mathsf {reg}}$
and
![]() $\tilde {\boldsymbol {\zeta }}\in \tilde {\mathfrak n}^{*}_{\mathsf {reg}}$
, it follows from (4.1) that
$\tilde {\boldsymbol {\zeta }}\in \tilde {\mathfrak n}^{*}_{\mathsf {reg}}$
, it follows from (4.1) that
![]() $\dim {\mathfrak n}^{\boldsymbol {\zeta }}=\dim (\tilde {\mathfrak n}/{\mathfrak n})+\dim \tilde {\mathfrak n}^{\tilde {\boldsymbol {\zeta }}}$
. Since
$\dim {\mathfrak n}^{\boldsymbol {\zeta }}=\dim (\tilde {\mathfrak n}/{\mathfrak n})+\dim \tilde {\mathfrak n}^{\tilde {\boldsymbol {\zeta }}}$
. Since
![]() $\tau $
is B-equivariant, we have
$\tau $
is B-equivariant, we have ![]() . If
. If ![]() , then
, then
![]() ${\mathfrak n}\subset \tilde {\mathfrak n}=\bigoplus _{j=1}^k{\mathfrak h}_j$
and
${\mathfrak n}\subset \tilde {\mathfrak n}=\bigoplus _{j=1}^k{\mathfrak h}_j$
and
![]() ${\mathfrak n}=\bigoplus _{j=1}^k ({\mathfrak h}_j\cap {\mathfrak n})$
(see Section 2.3). For any
${\mathfrak n}=\bigoplus _{j=1}^k ({\mathfrak h}_j\cap {\mathfrak n})$
(see Section 2.3). For any
![]() $\gamma \in \Delta ({\mathfrak h}_j)\setminus \{\beta _j\}=:\overline {\Delta ({\mathfrak h}_j)}$
, we have
$\gamma \in \Delta ({\mathfrak h}_j)\setminus \{\beta _j\}=:\overline {\Delta ({\mathfrak h}_j)}$
, we have
![]() $\beta _j-\gamma \in \Delta ^+$
.
$\beta _j-\gamma \in \Delta ^+$
.
Lemma 4.3 Under the previous notation, if
![]() ${\mathfrak n}\ne \tilde {\mathfrak n}$
and
${\mathfrak n}\ne \tilde {\mathfrak n}$
and ![]() , then the root space
, then the root space
![]() ${\mathfrak g}_{\beta _j-\gamma }$
belongs to
${\mathfrak g}_{\beta _j-\gamma }$
belongs to
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
.
${\mathfrak n}^{\boldsymbol {\zeta }}$
.
Proof Assume that
![]() $\beta _j-\gamma \not \in \Delta ({\mathfrak n})$
. Then
$\beta _j-\gamma \not \in \Delta ({\mathfrak n})$
. Then
![]() $[\gamma :\alpha ]=[\beta _j-\gamma :\alpha ]=0$
for all
$[\gamma :\alpha ]=[\beta _j-\gamma :\alpha ]=0$
for all ![]() . Hence,
. Hence,
![]() $[\beta _j:\alpha ]=0$
. However, since
$[\beta _j:\alpha ]=0$
. However, since
![]() $\beta _j\in \Delta ({\mathfrak n})$
, there is an
$\beta _j\in \Delta ({\mathfrak n})$
, there is an ![]() such that
such that
![]() $\beta _j\succ \alpha '$
, i.e.,
$\beta _j\succ \alpha '$
, i.e.,
![]() $[\beta _j:\alpha ']>0$
. This contradiction shows that
$[\beta _j:\alpha ']>0$
. This contradiction shows that
![]() $\gamma ':=\beta _j-\gamma \in \Delta ({\mathfrak n})$
.
$\gamma ':=\beta _j-\gamma \in \Delta ({\mathfrak n})$
.
Let us prove that
![]() ${\mathfrak g}_{\gamma '}\subset {\mathfrak n}^{\boldsymbol {\zeta }}$
. Since
${\mathfrak g}_{\gamma '}\subset {\mathfrak n}^{\boldsymbol {\zeta }}$
. Since
![]() $\gamma '\in \Delta ({\mathfrak h}_j)$
and hence
$\gamma '\in \Delta ({\mathfrak h}_j)$
and hence
![]() ${\mathsf {supp}}(\gamma ')\subset {\mathsf {supp}}(\beta _j)$
, properties of
${\mathsf {supp}}(\gamma ')\subset {\mathsf {supp}}(\beta _j)$
, properties of ![]() imply that
imply that
![]() $\beta _j$
is the only element
$\beta _j$
is the only element
![]() $\beta _i$
of
$\beta _i$
of ![]() such that
such that
![]() $\beta _i-\gamma '$
is a root. Indeed,
$\beta _i-\gamma '$
is a root. Indeed,
-
• if
 $\beta _i$
and
$\beta _i$
and
 $\beta _j$
are incomparable, then
$\beta _j$
are incomparable, then
 ${\mathsf {supp}}(\beta _i)\cap {\mathsf {supp}}(\beta _j)=\varnothing $
;
${\mathsf {supp}}(\beta _i)\cap {\mathsf {supp}}(\beta _j)=\varnothing $
; -
• if
 $\beta _i\prec \beta _j$
, then
$\beta _i\prec \beta _j$
, then
 ${\mathsf {supp}}(\beta _i)\subset {\mathsf {supp}}(\beta _j)\setminus \Phi (\beta _j)$
, while
${\mathsf {supp}}(\beta _i)\subset {\mathsf {supp}}(\beta _j)\setminus \Phi (\beta _j)$
, while
 ${\mathsf {supp}}(\gamma ')\cap \Phi (\beta _j)\ne \varnothing $
;
${\mathsf {supp}}(\gamma ')\cap \Phi (\beta _j)\ne \varnothing $
; -
• if
 $\beta _i\succ \beta _j$
, then
$\beta _i\succ \beta _j$
, then
 $(\beta _i,\gamma ')=0$
and
$(\beta _i,\gamma ')=0$
and
 $\gamma '$
does not belong to the Heisenberg subset of
$\gamma '$
does not belong to the Heisenberg subset of
 $\Delta \langle i\rangle $
.
$\Delta \langle i\rangle $
.
Therefore,
![]() $\gamma '-\beta _j=-\gamma $
is the only root that might occur in
$\gamma '-\beta _j=-\gamma $
is the only root that might occur in
![]() $[e_{\gamma '},{\boldsymbol {\zeta }}]$
. But
$[e_{\gamma '},{\boldsymbol {\zeta }}]$
. But
![]() $\gamma \not \in \Delta ({\mathfrak n})$
, i.e.,
$\gamma \not \in \Delta ({\mathfrak n})$
, i.e.,
![]() $-\gamma \not \in \Delta ({\mathfrak n}^{*})$
and therefore
$-\gamma \not \in \Delta ({\mathfrak n}^{*})$
and therefore
![]() $ {\mathrm {ad}}^{*} _{\mathfrak n}(e_{\gamma '})({\boldsymbol {\zeta }})=0$
.
$ {\mathrm {ad}}^{*} _{\mathfrak n}(e_{\gamma '})({\boldsymbol {\zeta }})=0$
.
Theorem 4.4 Let
![]() ${\mathfrak n}$
be an arbitrary nilradical and
${\mathfrak n}$
be an arbitrary nilradical and
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}_0\subset {\mathfrak n}^{*}$
a cascade point. Then:
${\boldsymbol {\zeta }}\in {\mathfrak k}_0\subset {\mathfrak n}^{*}$
a cascade point. Then:
-
(i)
 ${\mathfrak n}^{\boldsymbol {\zeta }}$
is T-stable and
${\mathfrak n}^{\boldsymbol {\zeta }}$
is T-stable and 
-
(ii)
 .
. -
(iii) For any
 $\xi \in {\mathfrak k}_0$
, we have
$\xi \in {\mathfrak k}_0$
, we have
 ${\mathfrak n}^{\xi }={\mathfrak n}^{\boldsymbol {\zeta }}$
.
${\mathfrak n}^{\xi }={\mathfrak n}^{\boldsymbol {\zeta }}$
.
Proof The number of roots in ![]() equals
equals
![]() $\dim (\tilde {\mathfrak n}/{\mathfrak n})=\dim {\mathfrak n}^{\boldsymbol {\zeta }}-\dim \tilde {\mathfrak n}^{\tilde {\boldsymbol {\zeta }}}$
, and each such root yields a root subspace in
$\dim (\tilde {\mathfrak n}/{\mathfrak n})=\dim {\mathfrak n}^{\boldsymbol {\zeta }}-\dim \tilde {\mathfrak n}^{\tilde {\boldsymbol {\zeta }}}$
, and each such root yields a root subspace in
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
(Lemma 4.3), hence (i). Clearly, (ii) is just a reformulation of (i). The last assertion follows from the fact that
${\mathfrak n}^{\boldsymbol {\zeta }}$
(Lemma 4.3), hence (i). Clearly, (ii) is just a reformulation of (i). The last assertion follows from the fact that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
is T-stable and
${\mathfrak n}^{\boldsymbol {\zeta }}$
is T-stable and
![]() $T{\cdot }{{\boldsymbol {\zeta }}}={\mathfrak k}_0$
.
$T{\cdot }{{\boldsymbol {\zeta }}}={\mathfrak k}_0$
.
The advantage of
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}_0$
is that
${\boldsymbol {\zeta }}\in {\mathfrak k}_0$
is that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
is a sum of root spaces. Therefore, Eq. (3.3) is easily verified in practice. It is convenient to restate it as follows.
${\mathfrak n}^{\boldsymbol {\zeta }}$
is a sum of root spaces. Therefore, Eq. (3.3) is easily verified in practice. It is convenient to restate it as follows.
Condition 4.5 The stabilizer
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
of
${\mathfrak n}^{\boldsymbol {\zeta }}$
of
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}_0\subset {\mathfrak n}^{*}$
is generic (equivalently,
${\boldsymbol {\zeta }}\in {\mathfrak k}_0\subset {\mathfrak n}^{*}$
is generic (equivalently,
![]() $({\mathfrak n}:{\mathfrak n}^{*})$
has a generic stabilizer) if and only if the difference of any two roots in
$({\mathfrak n}:{\mathfrak n}^{*})$
has a generic stabilizer) if and only if the difference of any two roots in
![]() $\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
does not belong to
$\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
does not belong to
![]() $\Delta ({\mathfrak n})$
.
$\Delta ({\mathfrak n})$
.
Example 4.6 (1) If
![]() ${\mathfrak g}=\mathfrak {sl}_7$
and
${\mathfrak g}=\mathfrak {sl}_7$
and ![]() , then
, then ![]() is not optimal and
is not optimal and ![]() , where
, where ![]() (see Example 2.5). Here,
(see Example 2.5). Here, ![]() and the matrices therein show that
and the matrices therein show that
![]() $\dim (\tilde {\mathfrak n}/{\mathfrak n})=4$
. More precisely,
$\dim (\tilde {\mathfrak n}/{\mathfrak n})=4$
. More precisely,

Therefore,
![]() $\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})=\{ \alpha _2, \alpha _2+\alpha _3, [2,4], [2,5], [2,6], [1,6]\}$
. Since
$\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})=\{ \alpha _2, \alpha _2+\alpha _3, [2,4], [2,5], [2,6], [1,6]\}$
. Since
![]() $[2,6]-\alpha _2=[3,6]\in \Delta ({\mathfrak n})$
, Condition 4.5 is not satisfied for
$[2,6]-\alpha _2=[3,6]\in \Delta ({\mathfrak n})$
, Condition 4.5 is not satisfied for
![]() ${\boldsymbol {\zeta }}$
, and
${\boldsymbol {\zeta }}$
, and
![]() $({\mathfrak n}:{\mathfrak n}^{*})$
does not have a generic stabilizer.
$({\mathfrak n}:{\mathfrak n}^{*})$
does not have a generic stabilizer.
(2) If
![]() ${\mathfrak g}=\mathfrak {sl}_7$
and
${\mathfrak g}=\mathfrak {sl}_7$
and ![]() , then
, then
![]() ${\mathfrak n}_{T_2}$
has the same optimization
${\mathfrak n}_{T_2}$
has the same optimization
![]() $\tilde {\mathfrak n}$
as
$\tilde {\mathfrak n}$
as ![]() , but now
, but now ![]() and
and ![]() . Here, Condition 4.5 is satisfied and
. Here, Condition 4.5 is satisfied and ![]() is a generic stabilizer.
is a generic stabilizer.
Thus, the action
![]() $(N:{\mathfrak n}^{*})$
does not always have N-generic stabilizers. A remedy is to consider the action of the larger group
$(N:{\mathfrak n}^{*})$
does not always have N-generic stabilizers. A remedy is to consider the action of the larger group
![]() $\tilde N$
on
$\tilde N$
on
![]() ${\mathfrak n}^{*}$
.
${\mathfrak n}^{*}$
.
Theorem 4.7 For any nilradical
![]() ${\mathfrak n}$
and the cascade subspace
${\mathfrak n}$
and the cascade subspace
![]() ${\mathfrak k}\subset {\mathfrak n}^{*}$
, we have:
${\mathfrak k}\subset {\mathfrak n}^{*}$
, we have:
-
(i)
 $\dim N{\cdot }{\mathfrak k}=2\dim {\mathfrak n}-\dim \tilde {\mathfrak n}$
, i.e.,
$\dim N{\cdot }{\mathfrak k}=2\dim {\mathfrak n}-\dim \tilde {\mathfrak n}$
, i.e.,
 ${\mathrm {codim\,}}_{{\mathfrak n}^{*}}N{\cdot }{\mathfrak k}=\dim (\tilde {\mathfrak n}/{\mathfrak n})$
;
${\mathrm {codim\,}}_{{\mathfrak n}^{*}}N{\cdot }{\mathfrak k}=\dim (\tilde {\mathfrak n}/{\mathfrak n})$
; -
(ii) the
 $\tilde N$
-saturation of
$\tilde N$
-saturation of
 ${\mathfrak k}$
is dense in
${\mathfrak k}$
is dense in
 ${\mathfrak n}^{*}$
, i.e.,
${\mathfrak n}^{*}$
, i.e.,
 $\overline {\tilde N{\cdot }{\mathfrak k}}={\mathfrak n}^{*}$
;
$\overline {\tilde N{\cdot }{\mathfrak k}}={\mathfrak n}^{*}$
; -
(iii)
 $\tilde {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}^{\boldsymbol {\zeta }}$
is a generic stabilizer for the linear action
$\tilde {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}^{\boldsymbol {\zeta }}$
is a generic stabilizer for the linear action
 $(\tilde N:{\mathfrak n}^{*})$
.
$(\tilde N:{\mathfrak n}^{*})$
.
Proof Recall that
![]() $\dim {\mathfrak k}={\mathrm {ind}}\,\tilde {\mathfrak n}$
and
$\dim {\mathfrak k}={\mathrm {ind}}\,\tilde {\mathfrak n}$
and
![]() $\max _{\xi \in {\mathfrak n}^{*}}\dim N{\cdot }\xi =\dim N{\cdot }{\boldsymbol {\zeta }}=\dim {\mathfrak n}-{\mathrm {ind}}\,{\mathfrak n}$
.
$\max _{\xi \in {\mathfrak n}^{*}}\dim N{\cdot }\xi =\dim N{\cdot }{\boldsymbol {\zeta }}=\dim {\mathfrak n}-{\mathrm {ind}}\,{\mathfrak n}$
.
(i) Since
![]() $\mathsf T_{\boldsymbol {\zeta }}(N{\cdot }{\boldsymbol {\zeta }})={\mathfrak n}{\cdot }{\boldsymbol {\zeta }}=({\mathfrak n}^{\boldsymbol {\zeta }})^{\perp }$
, it follows from Theorem 4.4
(iii) that all tangent spaces
$\mathsf T_{\boldsymbol {\zeta }}(N{\cdot }{\boldsymbol {\zeta }})={\mathfrak n}{\cdot }{\boldsymbol {\zeta }}=({\mathfrak n}^{\boldsymbol {\zeta }})^{\perp }$
, it follows from Theorem 4.4
(iii) that all tangent spaces
![]() ${\mathfrak n}{\cdot }\xi $
,
${\mathfrak n}{\cdot }\xi $
,
![]() $\xi \in {\mathfrak k}_0$
, are the same. Therefore, using the differential of the map
$\xi \in {\mathfrak k}_0$
, are the same. Therefore, using the differential of the map
at
![]() $(1,{\boldsymbol {\zeta }})$
, we obtain
$(1,{\boldsymbol {\zeta }})$
, we obtain
![]() $\dim \overline {N{\cdot }{\mathfrak k}}=\dim ({\mathsf {Im\,}} \textit {d}\kappa _{(1,{\boldsymbol {\zeta }})})= \dim ({\mathfrak n}{\cdot }{\boldsymbol {\zeta }}+{\mathfrak k})$
. Because the roots in
$\dim \overline {N{\cdot }{\mathfrak k}}=\dim ({\mathsf {Im\,}} \textit {d}\kappa _{(1,{\boldsymbol {\zeta }})})= \dim ({\mathfrak n}{\cdot }{\boldsymbol {\zeta }}+{\mathfrak k})$
. Because the roots in ![]() are strongly orthogonal, we have
are strongly orthogonal, we have
![]() ${\mathfrak n}{\cdot }{\boldsymbol {\zeta }}\cap {\mathfrak k}=\{0\}$
and hence
${\mathfrak n}{\cdot }{\boldsymbol {\zeta }}\cap {\mathfrak k}=\{0\}$
and hence
(ii) Since
![]() $\tilde N{\cdot }\tilde {\mathfrak k}$
is dense in
$\tilde N{\cdot }\tilde {\mathfrak k}$
is dense in
![]() $\tilde {\mathfrak n}^{*}$
(Proposition 4.2) and
$\tilde {\mathfrak n}^{*}$
(Proposition 4.2) and
![]() $\tau $
is B-equivariant, we conclude that
$\tau $
is B-equivariant, we conclude that
![]() $\tau (\tilde N{\cdot }\tilde {\mathfrak k})=\tilde N{\cdot }{\mathfrak k}$
is dense in
$\tau (\tilde N{\cdot }\tilde {\mathfrak k})=\tilde N{\cdot }{\mathfrak k}$
is dense in
![]() $\tau (\tilde {\mathfrak n}^{*})={\mathfrak n}^{*}$
.
$\tau (\tilde {\mathfrak n}^{*})={\mathfrak n}^{*}$
.
(iii) Let us first prove that
Clearly, inequality “
![]() $\leqslant $
” holds. By Eq. (4.1), the RHS equals
$\leqslant $
” holds. By Eq. (4.1), the RHS equals
![]() $\dim \tilde {\mathfrak n}-{\mathrm {ind}}\,{\mathfrak n}=\dim {\mathfrak n}-\dim {\mathfrak k}$
. On the other hand, part (ii) implies that
$\dim \tilde {\mathfrak n}-{\mathrm {ind}}\,{\mathfrak n}=\dim {\mathfrak n}-\dim {\mathfrak k}$
. On the other hand, part (ii) implies that
![]() $\dim {\mathfrak n}=\dim \tilde N{\cdot }{\mathfrak k}\leqslant \max _{\xi \in {\mathfrak k}}\dim \tilde N{\cdot }\xi +\dim {\mathfrak k}$
. This proves Eq. (4.2) and also shows that almost all
$\dim {\mathfrak n}=\dim \tilde N{\cdot }{\mathfrak k}\leqslant \max _{\xi \in {\mathfrak k}}\dim \tilde N{\cdot }\xi +\dim {\mathfrak k}$
. This proves Eq. (4.2) and also shows that almost all
![]() $\xi \in {\mathfrak k}$
satisfy this relation. Moreover, since
$\xi \in {\mathfrak k}$
satisfy this relation. Moreover, since
![]() ${\mathfrak k}$
is T-stable and
${\mathfrak k}$
is T-stable and
![]() ${\mathfrak k}_0=T{\cdot }{\boldsymbol {\zeta }}$
is dense in
${\mathfrak k}_0=T{\cdot }{\boldsymbol {\zeta }}$
is dense in
![]() ${\mathfrak k}$
, we obtain that
${\mathfrak k}$
, we obtain that
for every
![]() $\xi \in {\mathfrak k}_0$
. Hence,
$\xi \in {\mathfrak k}_0$
. Hence,
![]() $\tilde {\mathfrak n}^{\xi }={\mathfrak n}^{\xi }$
for every
$\tilde {\mathfrak n}^{\xi }={\mathfrak n}^{\xi }$
for every
![]() $\xi \in {\mathfrak k}_0$
. Combining this with Theorem 4.4
(iii) and part (ii), we conclude that
$\xi \in {\mathfrak k}_0$
. Combining this with Theorem 4.4
(iii) and part (ii), we conclude that
![]() $\tilde {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}^{\boldsymbol {\zeta }}$
is a generic stabilizer for the action
$\tilde {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}^{\boldsymbol {\zeta }}$
is a generic stabilizer for the action
![]() $(\tilde N:{\mathfrak n}^{*})$
.
$(\tilde N:{\mathfrak n}^{*})$
.
Using Theorem 4.4, we describe certain nilradicals that do not have a generic stabilizer.
Proposition 4.8 Let
![]() $\beta _j$
be a descendant of
$\beta _j$
be a descendant of ![]() and
and
![]() $\alpha \in \Phi (\beta _i)$
. Suppose that
$\alpha \in \Phi (\beta _i)$
. Suppose that ![]() and
and
![]() $[\beta _i:\nu ]>[\beta _j:\nu ]>0$
for some
$[\beta _i:\nu ]>[\beta _j:\nu ]>0$
for some ![]() . Then
. Then ![]() does not have a generic stabilizer.
does not have a generic stabilizer.
Proof Recall that
![]() $\beta _i$
is the highest root in
$\beta _i$
is the highest root in
![]() $\Delta \langle i\rangle ^+$
and
$\Delta \langle i\rangle ^+$
and
![]() $\beta _j$
is a maximal root in
$\beta _j$
is a maximal root in
![]() $\Delta \langle i\rangle ^+\setminus \Delta ({\mathfrak h}_i)$
. If
$\Delta \langle i\rangle ^+\setminus \Delta ({\mathfrak h}_i)$
. If
![]() $\Phi (\beta _i)=\{\alpha \}$
, then
$\Phi (\beta _i)=\{\alpha \}$
, then
![]() $\alpha +\beta _j\in \Delta ({\mathfrak h}_i)\subset \Delta \langle i\rangle ^+$
, because
$\alpha +\beta _j\in \Delta ({\mathfrak h}_i)\subset \Delta \langle i\rangle ^+$
, because
![]() $\beta _j$
is not the highest root of
$\beta _j$
is not the highest root of
![]() $\Delta \langle i\rangle ^+$
. If
$\Delta \langle i\rangle ^+$
. If
![]() $\Phi (\beta _i)=\{\alpha ,\alpha '\}$
, then
$\Phi (\beta _i)=\{\alpha ,\alpha '\}$
, then
![]() $\Delta \langle i\rangle $
is of type
$\Delta \langle i\rangle $
is of type
![]() ${\mathsf {\mathbf {{A}}}}_{p}$
and hence both
${\mathsf {\mathbf {{A}}}}_{p}$
and hence both
![]() $\beta _j+\alpha $
and
$\beta _j+\alpha $
and
![]() $\beta _j+\alpha '$
belong to
$\beta _j+\alpha '$
belong to
![]() $\Delta ({\mathfrak h}_i)$
. In any case, if
$\Delta ({\mathfrak h}_i)$
. In any case, if
![]() $\alpha \in \Phi (\beta _i)$
, then
$\alpha \in \Phi (\beta _i)$
, then
![]() $\beta _i-\alpha -\beta _j\in \Delta ^+$
.
$\beta _i-\alpha -\beta _j\in \Delta ^+$
.
Since ![]() and
and
![]() $[\beta _j:\nu ]>0$
, we have
$[\beta _j:\nu ]>0$
, we have
![]() $\beta _j\in \Delta ({\mathfrak n})$
and also
$\beta _j\in \Delta ({\mathfrak n})$
and also
![]() $\beta _i\in \Delta ({\mathfrak n})$
. That is,
$\beta _i\in \Delta ({\mathfrak n})$
. That is, ![]() . Because
. Because
![]() $\alpha \in \Delta ({\mathfrak h}_i)\setminus \Delta ({\mathfrak n})$
, we have
$\alpha \in \Delta ({\mathfrak h}_i)\setminus \Delta ({\mathfrak n})$
, we have
![]() $\beta _i-\alpha \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
(see Theorem 4.4
(ii)). The assumption on
$\beta _i-\alpha \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
(see Theorem 4.4
(ii)). The assumption on
![]() $\nu $
implies that
$\nu $
implies that
![]() $[\beta _i-\alpha -\beta _j:\nu ]>0$
. Thus, we have
$[\beta _i-\alpha -\beta _j:\nu ]>0$
. Thus, we have
![]() $\beta _i-\alpha ,\beta _j\in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
and
$\beta _i-\alpha ,\beta _j\in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
and
![]() $\beta _i-\alpha -\beta _j\in \Delta ({\mathfrak n})$
. By Condition 4.5, this means that
$\beta _i-\alpha -\beta _j\in \Delta ({\mathfrak n})$
. By Condition 4.5, this means that
![]() ${\mathfrak n}$
has no generic stabilizers.
${\mathfrak n}$
has no generic stabilizers.
Example 4.9 For applications, it suffices to consider the case in which
![]() $\beta _i=\theta $
, i.e.,
$\beta _i=\theta $
, i.e.,
![]() $i=1$
.
$i=1$
.
(1) If
![]() ${\mathfrak g}$
is exceptional, then
${\mathfrak g}$
is exceptional, then
![]() $\#\Phi (\beta _1)=1$
and
$\#\Phi (\beta _1)=1$
and
![]() $\beta _1$
has the unique descendant
$\beta _1$
has the unique descendant
![]() $\beta _2$
. Although
$\beta _2$
. Although
![]() $\beta _1-\beta _2$
is not a root, its support is defined as in Section 2.1. Then Proposition 4.8 applies to any
$\beta _1-\beta _2$
is not a root, its support is defined as in Section 2.1. Then Proposition 4.8 applies to any
![]() $\nu \in {\mathsf {supp}}(\beta _1-\beta _2)\setminus \Phi (\beta _1)$
and
$\nu \in {\mathsf {supp}}(\beta _1-\beta _2)\setminus \Phi (\beta _1)$
and ![]() .
.
For instance, let
![]() ${\mathfrak g}$
be of type
${\mathfrak g}$
be of type
![]() ${\mathsf {\mathbf {{E}}}}_{6}$
. Then
${\mathsf {\mathbf {{E}}}}_{6}$
. Then
![]() $\Phi (\beta _1)=\{\alpha _6\}$
,
$\Phi (\beta _1)=\{\alpha _6\}$
,
![]() ${\mathsf {supp}}(\beta _1-\beta _2)=\{\alpha _2,\alpha _3,\alpha _4,\alpha _6\}$
, and
${\mathsf {supp}}(\beta _1-\beta _2)=\{\alpha _2,\alpha _3,\alpha _4,\alpha _6\}$
, and
![]() ${\mathsf {supp}}(\beta _2)\supset \{\alpha _2,\alpha _3,\alpha _4\}$
(see formulae for
${\mathsf {supp}}(\beta _2)\supset \{\alpha _2,\alpha _3,\alpha _4\}$
(see formulae for ![]() in Appendix A). Hence, one can take
in Appendix A). Hence, one can take
![]() $\nu =\alpha _i$
with
$\nu =\alpha _i$
with
![]() $i\in \{2,3,4\}$
. More generally, if
$i\in \{2,3,4\}$
. More generally, if ![]() and
and ![]() , then
, then ![]() has no generic stabilizers.
has no generic stabilizers.
(2) This method also works for
![]() ${\mathfrak g}={\mathfrak {so}}_{n}$
with
${\mathfrak g}={\mathfrak {so}}_{n}$
with
![]() $n\geqslant 7$
, where
$n\geqslant 7$
, where
![]() $\Phi (\beta _1)=\{\alpha _2\}$
.
$\Phi (\beta _1)=\{\alpha _2\}$
.
– If
![]() $n\ne 8$
, then
$n\ne 8$
, then
![]() $\beta _1=\varepsilon _1+\varepsilon _2$
has two descendants,
$\beta _1=\varepsilon _1+\varepsilon _2$
has two descendants,
![]() $\beta _2=\varepsilon _1-\varepsilon _2$
, and
$\beta _2=\varepsilon _1-\varepsilon _2$
, and
![]() $\beta _3=\varepsilon _3+\varepsilon _4$
(
$\beta _3=\varepsilon _3+\varepsilon _4$
(
![]() $\varepsilon _4=0$
, if
$\varepsilon _4=0$
, if
![]() $n=7$
) (see Appendix A). For
$n=7$
) (see Appendix A). For
![]() $(\beta _1,\beta _3)$
, Proposition 4.8 applies, if one takes
$(\beta _1,\beta _3)$
, Proposition 4.8 applies, if one takes ![]() . While for
. While for
![]() $(\beta _1,\beta _2)$
, we can take
$(\beta _1,\beta _2)$
, we can take ![]() such that
such that ![]() and
and ![]() with
with
![]() $j\geqslant 3$
.
$j\geqslant 3$
.
– If
![]() $n=8$
, then
$n=8$
, then
![]() $\beta _1$
has three descendants, and we can take
$\beta _1$
has three descendants, and we can take ![]() with
with
![]() $i,j\ne 2$
.
$i,j\ne 2$
.
Proposition 4.10 If
![]() ${\mathfrak n}\subset {\mathfrak n}'$
and
${\mathfrak n}\subset {\mathfrak n}'$
and
![]() $\tilde {\mathfrak n}=\tilde {{\mathfrak n}'}$
, then
$\tilde {\mathfrak n}=\tilde {{\mathfrak n}'}$
, then
![]() ${\mathcal F}({\mathfrak n}')\subset {\mathcal F}({\mathfrak n})\subset {\mathfrak n}$
.
${\mathcal F}({\mathfrak n}')\subset {\mathcal F}({\mathfrak n})\subset {\mathfrak n}$
.
Proof Let
![]() ${\mathfrak k}$
(resp.
${\mathfrak k}$
(resp.
![]() ${\mathfrak k}'$
) be the cascade subspace of
${\mathfrak k}'$
) be the cascade subspace of
![]() ${\mathfrak n}^{*}$
(resp.
${\mathfrak n}^{*}$
(resp.
![]() $({\mathfrak n}')^{*}$
). Take
$({\mathfrak n}')^{*}$
). Take
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}_0$
and
${\boldsymbol {\zeta }}\in {\mathfrak k}_0$
and
![]() ${\boldsymbol {\zeta }}'\in {\mathfrak k}^{\prime }_0$
. Since
${\boldsymbol {\zeta }}'\in {\mathfrak k}^{\prime }_0$
. Since
![]() $\Delta ({\mathfrak n})\subset \Delta ({\mathfrak n}')$
and
$\Delta ({\mathfrak n})\subset \Delta ({\mathfrak n}')$
and ![]() , we have
, we have ![]() for all
for all ![]() . Then Theorem 4.4 shows that
. Then Theorem 4.4 shows that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}\supset ({\mathfrak n}')^{{\boldsymbol {\zeta }}'}$
. By Proposition 4.1, this yields the required embedding.
${\mathfrak n}^{\boldsymbol {\zeta }}\supset ({\mathfrak n}')^{{\boldsymbol {\zeta }}'}$
. By Proposition 4.1, this yields the required embedding.
Our description of
![]() $\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
yields a criterion for
$\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
yields a criterion for
![]() ${\mathfrak n}$
to be quasi-quadratic.
${\mathfrak n}$
to be quasi-quadratic.
Theorem 4.11 For a nilradical ![]() , the following assertions are equivalent:
, the following assertions are equivalent:
-
•
 ${\mathcal F}({\mathfrak n})={\mathfrak n}$
, i.e.,
${\mathcal F}({\mathfrak n})={\mathfrak n}$
, i.e.,
 ${\mathfrak n}$
is quasi-quadratic.
${\mathfrak n}$
is quasi-quadratic. -
• For each
 , one of the two conditions is satisfied:
, one of the two conditions is satisfied:-
– either
 ;
; -
– or
 $\Phi (\Phi ^{-1}(\alpha ))=\{\alpha ,\alpha '\}$
, and if C is the chain in the Dynkin diagram that connects
$\Phi (\Phi ^{-1}(\alpha ))=\{\alpha ,\alpha '\}$
, and if C is the chain in the Dynkin diagram that connects
 $\alpha $
and
$\alpha $
and
 $\alpha '$
, then
$\alpha '$
, then  (in particular,
(in particular,  ).
).
-
Proof Since
![]() ${\mathcal F}({\mathfrak n})$
is the
${\mathcal F}({\mathfrak n})$
is the
![]() ${\mathfrak b}$
-ideal generated by
${\mathfrak b}$
-ideal generated by
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
(Proposition 4.1), it is clear that
${\mathfrak n}^{\boldsymbol {\zeta }}$
(Proposition 4.1), it is clear that
![]() ${\mathcal F}({\mathfrak n})={\mathfrak n}$
if and only if
${\mathcal F}({\mathfrak n})={\mathfrak n}$
if and only if
![]() $\alpha \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
for each
$\alpha \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
for each ![]() .
.
(1) If ![]() , then
, then
![]() $\Phi (\alpha )=\alpha $
and
$\Phi (\alpha )=\alpha $
and
![]() $\alpha \in \Delta (\tilde {\mathfrak n}^{\boldsymbol {\zeta }})\subset \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
.
$\alpha \in \Delta (\tilde {\mathfrak n}^{\boldsymbol {\zeta }})\subset \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
.
(2) If ![]() and
and ![]() , then
, then
![]() $\alpha \ne \beta _j$
and there are two possibilities.
$\alpha \ne \beta _j$
and there are two possibilities.
–
![]() $\Phi (\beta _j)=\alpha $
. Then the whole Heisenberg algebra
$\Phi (\beta _j)=\alpha $
. Then the whole Heisenberg algebra
![]() ${\mathfrak h}_{j}$
belongs to
${\mathfrak h}_{j}$
belongs to
![]() ${\mathfrak n}$
and hence
${\mathfrak n}$
and hence ![]() . Then it follows from Theorem 4.4
(ii) that
. Then it follows from Theorem 4.4
(ii) that
![]() $\Delta ({\mathfrak h}_j\cap {\mathfrak n}^{\boldsymbol {\zeta }})=\{\beta _j\}$
, i.e.,
$\Delta ({\mathfrak h}_j\cap {\mathfrak n}^{\boldsymbol {\zeta }})=\{\beta _j\}$
, i.e.,
![]() $\alpha \not \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
.
$\alpha \not \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
.
–
![]() $\Phi (\beta _j)=\{\alpha , \alpha '\}$
. Here,
$\Phi (\beta _j)=\{\alpha , \alpha '\}$
. Here,
![]() $\beta _j$
is the highest root in a root system of type
$\beta _j$
is the highest root in a root system of type
![]() ${\mathsf {\mathbf {{A}}}}_{p}$
(
${\mathsf {\mathbf {{A}}}}_{p}$
(
![]() $p\geqslant 2$
). Therefore, if
$p\geqslant 2$
). Therefore, if
![]() $C=\{\alpha =\alpha _1,\alpha _2,\dots ,\alpha _p=\alpha '\}$
is the chain connecting
$C=\{\alpha =\alpha _1,\alpha _2,\dots ,\alpha _p=\alpha '\}$
is the chain connecting
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
, then
$\alpha '$
, then
![]() $\beta _j=\alpha _1+\alpha _2+\dots +\alpha _p$
. Then
$\beta _j=\alpha _1+\alpha _2+\dots +\alpha _p$
. Then
![]() $\alpha \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
if and only if
$\alpha \in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
if and only if
![]() $\beta _j-\alpha =\alpha _2+\dots +\alpha _p\not \in \Delta ({\mathfrak n})$
, and this is only possible if
$\beta _j-\alpha =\alpha _2+\dots +\alpha _p\not \in \Delta ({\mathfrak n})$
, and this is only possible if ![]() .
.
Using Theorem 4.11, one readily obtains the list of all quasi-quadratic nilradicals.
Proposition 4.12 The quasi-quadratic nilradicals are as follows.
-
(1) If
 ${\mathfrak g}$
is not of type
${\mathfrak g}$
is not of type
 ${\mathsf {\mathbf {{A}}}}_{n},{\mathsf {\mathbf {{D}}}}_{2n+1},\text { and } {\mathsf {\mathbf {{E}}}}_{6}$
, then
${\mathsf {\mathbf {{A}}}}_{n},{\mathsf {\mathbf {{D}}}}_{2n+1},\text { and } {\mathsf {\mathbf {{E}}}}_{6}$
, then  if and only if
if and only if  .
. -
(2) If
 ${\mathfrak g}$
is of type
${\mathfrak g}$
is of type
 ${\mathsf {\mathbf {{A}}}}_{n}$
, then
${\mathsf {\mathbf {{A}}}}_{n}$
, then  if and only if
if and only if  ,
,
 $i=1,2,\dots ,n$
.
$i=1,2,\dots ,n$
. -
(3) If
 ${\mathfrak g}$
is of type
${\mathfrak g}$
is of type
 ${\mathsf {\mathbf {{D}}}}_{2n+1}$
, then
${\mathsf {\mathbf {{D}}}}_{2n+1}$
, then  if and only if
if and only if  and
and  .
. -
(4) If
 ${\mathfrak g}$
is of type
${\mathfrak g}$
is of type
 ${\mathsf {\mathbf {{E}}}}_{6}$
, then
${\mathsf {\mathbf {{E}}}}_{6}$
, then  if and only if
if and only if  ,
,
 $i\ne 6$
.
$i\ne 6$
.
Proof (1) In this case,
![]() $\Phi ^{-1}$
is a bijection; hence,
$\Phi ^{-1}$
is a bijection; hence,
![]() $\Phi (\Phi ^{-1}(\alpha ))=\{\alpha \}$
for any
$\Phi (\Phi ^{-1}(\alpha ))=\{\alpha \}$
for any
![]() $\alpha \in \Pi $
.
$\alpha \in \Pi $
.
(2) Here, each
![]() ${\mathfrak n}$
has a CP [Reference Elashvili and Ooms10]; hence,
${\mathfrak n}$
has a CP [Reference Elashvili and Ooms10]; hence,
![]() ${\mathcal F}({\mathfrak n})$
is abelian. That is,
${\mathcal F}({\mathfrak n})$
is abelian. That is,
![]() ${\mathcal F}({\mathfrak n})={\mathfrak n}$
must be an abelian nilradical.
${\mathcal F}({\mathfrak n})={\mathfrak n}$
must be an abelian nilradical.
(3) In this case, ![]() and there is a unique
and there is a unique ![]() such that
such that
![]() $\#\Phi (\beta )=2$
. Namely,
$\#\Phi (\beta )=2$
. Namely,
![]() $\Phi (\beta _{2n-1})=\{\alpha _{2n},\alpha _{2n+1}\}$
(see Appendix A). The chain connecting
$\Phi (\beta _{2n-1})=\{\alpha _{2n},\alpha _{2n+1}\}$
(see Appendix A). The chain connecting
![]() $\alpha _{2n}$
and
$\alpha _{2n}$
and
![]() $\alpha _{2n+1}$
in the Dynkin diagram is
$\alpha _{2n+1}$
in the Dynkin diagram is
![]() $C=\{\alpha _{2n},\alpha _{2n-1}, \alpha _{2n+1}\}$
. Hence the answer.
$C=\{\alpha _{2n},\alpha _{2n-1}, \alpha _{2n+1}\}$
. Hence the answer.
(4) Here, ![]() ,
,
![]() $\Phi (\beta _3)=\{\alpha _2,\alpha _4\}$
,
$\Phi (\beta _3)=\{\alpha _2,\alpha _4\}$
,
![]() $\Phi (\beta _2)=\{\alpha _1,\alpha _5\}$
(see Appendix A). Since
$\Phi (\beta _2)=\{\alpha _1,\alpha _5\}$
(see Appendix A). Since
![]() $\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5$
form a chain in the Dynkin diagram, the result follows.
$\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5$
form a chain in the Dynkin diagram, the result follows.
5 Generic stabilizers and the Frobenius semiradical in case of
 ${\mathfrak {sl}}_{n+1}$
or
${\mathfrak {sl}}_{n+1}$
or
 ${\mathfrak {sp}}_{2n}$
${\mathfrak {sp}}_{2n}$
First, we explicitly describe the nilradicals in
![]() ${\mathfrak {sl}}_{n+1}$
or
${\mathfrak {sl}}_{n+1}$
or
![]() ${\mathfrak {sp}}_{2n}$
having a generic stabilizer. To state the result for
${\mathfrak {sp}}_{2n}$
having a generic stabilizer. To state the result for
![]() ${\mathfrak {sl}}_{n+1}$
, we need some notation. Recall that, for
${\mathfrak {sl}}_{n+1}$
, we need some notation. Recall that, for
![]() ${\mathfrak {sl}}_{n+1}$
, the poset
${\mathfrak {sl}}_{n+1}$
, the poset ![]() is a chain
is a chain
![]() $\beta _1\succ \beta _2\succ \dots \succ \beta _t$
, where
$\beta _1\succ \beta _2\succ \dots \succ \beta _t$
, where
![]() $t=[(n+1)/2]$
and
$t=[(n+1)/2]$
and
![]() $\Phi (\beta _i)=\{\alpha _i,\alpha _{n+1-i}\}$
. Let
$\Phi (\beta _i)=\{\alpha _i,\alpha _{n+1-i}\}$
. Let ![]() be a nilradical. Then
be a nilradical. Then ![]() for some
for some
![]() $k\leqslant t$
(cf. Lemma 2.2). Therefore,
$k\leqslant t$
(cf. Lemma 2.2). Therefore, ![]() and
and ![]() . Set
. Set ![]() and
and ![]() .
.
Theorem 5.1 Suppose that
![]() ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
and
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
and ![]() . Then
. Then
(That is,
![]() $\sigma (\alpha _j)=\alpha _{n+1-j}$
.) In particular, if
$\sigma (\alpha _j)=\alpha _{n+1-j}$
.) In particular, if ![]() , then
, then ![]() has a generic stabilizer.
has a generic stabilizer.
Proof
1
![]() $^o$
. For
$^o$
. For
![]() $k=1$
, we have
$k=1$
, we have ![]() and
and
![]() ${\mathfrak n}\subset {\mathfrak h}_1$
. If
${\mathfrak n}\subset {\mathfrak h}_1$
. If ![]() , then
, then
![]() ${\mathfrak n}={\mathfrak h}_1$
is optimal. If
${\mathfrak n}={\mathfrak h}_1$
is optimal. If ![]() , then
, then
![]() ${\mathfrak n}$
is abelian. In both cases, there is a generic stabilizer for
${\mathfrak n}$
is abelian. In both cases, there is a generic stabilizer for
![]() $({\mathfrak n}:{\mathfrak n}^{*})$
, as required.
$({\mathfrak n}:{\mathfrak n}^{*})$
, as required.
2
![]() $^o$
. Suppose that
$^o$
. Suppose that
![]() $k\geqslant 2$
and the symmetry of
$k\geqslant 2$
and the symmetry of ![]() and
and ![]() fails for some
fails for some
![]() $j\leqslant k-1$
. W.l.o.g, we may assume that
$j\leqslant k-1$
. W.l.o.g, we may assume that ![]() , whereas
, whereas ![]() . Then
. Then
![]() $\beta _j-\alpha _{n+1-j}=\beta _{j+1}+\alpha _j\in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
. Since
$\beta _j-\alpha _{n+1-j}=\beta _{j+1}+\alpha _j\in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
. Since ![]() and
and
![]() $\alpha _j\in \Delta ({\mathfrak n})$
, Condition 4.5 is not satisfied.
$\alpha _j\in \Delta ({\mathfrak n})$
, Condition 4.5 is not satisfied.
3
![]() $^o$
. If
$^o$
. If ![]() , then one can directly describe
, then one can directly describe
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
and see that Condition 4.5 is satisfied. It is necessary to distinguish two cases: (a)
${\mathfrak n}^{\boldsymbol {\zeta }}$
and see that Condition 4.5 is satisfied. It is necessary to distinguish two cases: (a) ![]() and (b) only
and (b) only ![]() .
.
(a) Here, ![]() and
and
![]() $\Phi (\beta _k)\subset \Delta ({\mathfrak n})$
. Hence,
$\Phi (\beta _k)\subset \Delta ({\mathfrak n})$
. Hence,
![]() ${\mathfrak h}_k\subset {\mathfrak n}$
and
${\mathfrak h}_k\subset {\mathfrak n}$
and ![]() . Theorem 4.4
(ii) shows that
. Theorem 4.4
(ii) shows that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
, the last intersection being the north-east
${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
, the last intersection being the north-east
![]() $k\times k$
square of
$k\times k$
square of
![]() $(n+1)\times (n+1)$
matrices in
$(n+1)\times (n+1)$
matrices in
![]() ${\mathfrak {sl}}_{n+1}$
. More precisely, if
${\mathfrak {sl}}_{n+1}$
. More precisely, if ![]() , then
, then
![]() $\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})=\Gamma _1\cup \dots \cup \Gamma _j$
, where
$\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})=\Gamma _1\cup \dots \cup \Gamma _j$
, where
 $$ \begin{gather*} \Gamma_1=\{\varepsilon_i-\varepsilon_j \mid 1\leqslant i\leqslant i_1, \ n+2-i_1\leqslant j\leqslant n+1\} , \\ \Gamma_2=\{\varepsilon_i-\varepsilon_j \mid i_1+1\leqslant i\leqslant i_2, \ n+2-i_2\leqslant j\leqslant n+1-i_1\}, \text{etc.} \end{gather*} $$
$$ \begin{gather*} \Gamma_1=\{\varepsilon_i-\varepsilon_j \mid 1\leqslant i\leqslant i_1, \ n+2-i_1\leqslant j\leqslant n+1\} , \\ \Gamma_2=\{\varepsilon_i-\varepsilon_j \mid i_1+1\leqslant i\leqslant i_2, \ n+2-i_2\leqslant j\leqslant n+1-i_1\}, \text{etc.} \end{gather*} $$
Here,
![]() $\{\Gamma _s\}_{s=1}^j$
is a string of square blocks located along the antidiagonal in the
$\{\Gamma _s\}_{s=1}^j$
is a string of square blocks located along the antidiagonal in the
![]() $k\times k$
square (see Figure 1a). The size of the sth square is
$k\times k$
square (see Figure 1a). The size of the sth square is
![]() $i_s-i_{s-1}$
, where
$i_s-i_{s-1}$
, where
![]() $i_0=0$
. It is readily seen that if
$i_0=0$
. It is readily seen that if
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
belong to different blocks, then
$\gamma '$
belong to different blocks, then
![]() $\gamma -\gamma '$
is not a root, while if
$\gamma -\gamma '$
is not a root, while if
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
belong to the same block, then
$\gamma '$
belong to the same block, then
![]() $\gamma -\gamma '$
is either not a root or a root of the standard Levi subalgebra corresponding to
$\gamma -\gamma '$
is either not a root or a root of the standard Levi subalgebra corresponding to
![]() ${\mathfrak n}$
. Thus,
${\mathfrak n}$
. Thus,
![]() $\gamma -\gamma '\not \in \Delta ({\mathfrak n})$
and Condition 4.5 is satisfied.
$\gamma -\gamma '\not \in \Delta ({\mathfrak n})$
and Condition 4.5 is satisfied.
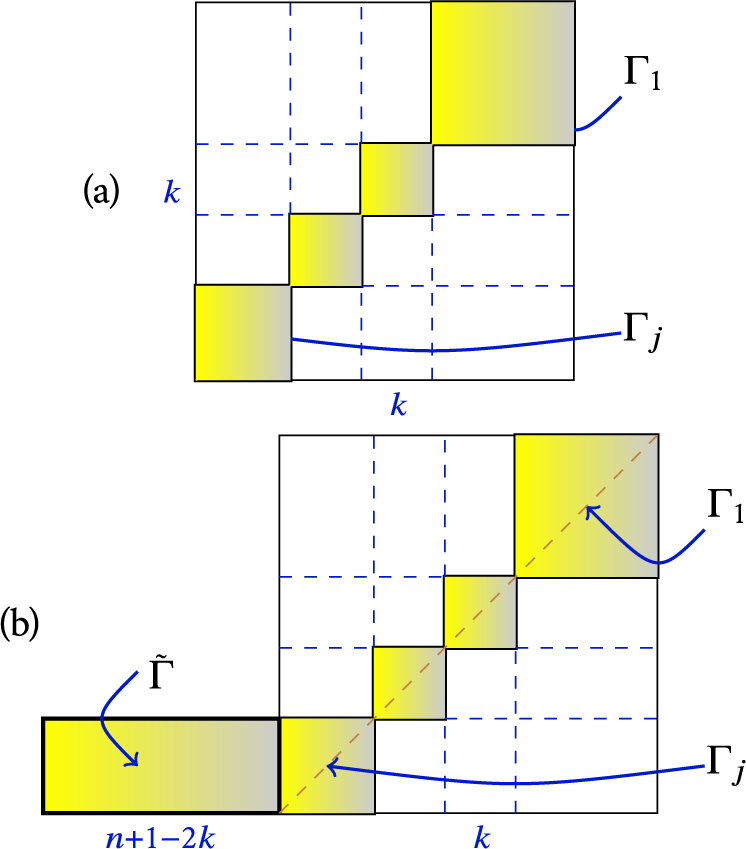
Figure 1: The generic stabilizer
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
: cases (a) and (b).
${\mathfrak n}^{\boldsymbol {\zeta }}$
: cases (a) and (b).
(b) Here,
![]() ${\mathfrak n}$
is smaller than in part (a), but
${\mathfrak n}$
is smaller than in part (a), but ![]() remains the same. Now only “half” of
remains the same. Now only “half” of
![]() ${\mathfrak h}_k$
belongs to
${\mathfrak h}_k$
belongs to
![]() ${\mathfrak n}$
. Therefore,
${\mathfrak n}$
. Therefore, ![]() , and the subsets
, and the subsets ![]() with
with
![]() $i_{j-1}< s< k$
become larger than in (a). Hence,
$i_{j-1}< s< k$
become larger than in (a). Hence,
![]() $\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
becomes larger and, along with
$\Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
becomes larger and, along with
![]() $\Gamma _1\cup \dots \cup \Gamma _j$
, it also contains the strip of roots
$\Gamma _1\cup \dots \cup \Gamma _j$
, it also contains the strip of roots
attached to
![]() $\Gamma _j$
(see Figure 1b). The new feature is that the difference of roots from
$\Gamma _j$
(see Figure 1b). The new feature is that the difference of roots from
![]() $\Gamma _j$
and
$\Gamma _j$
and
![]() $\tilde \Gamma $
can be a root in
$\tilde \Gamma $
can be a root in
![]() $\bigcup _{s=i_{j-1}}^k \Delta ({\mathfrak h}_s)$
. But such a difference belongs to the parts of sets
$\bigcup _{s=i_{j-1}}^k \Delta ({\mathfrak h}_s)$
. But such a difference belongs to the parts of sets
![]() $\Delta ({\mathfrak h}_s)$
that are missing in
$\Delta ({\mathfrak h}_s)$
that are missing in
![]() $\Delta ({\mathfrak n})$
. Thus, Condition 4.5 is still satisfied here.
$\Delta ({\mathfrak n})$
. Thus, Condition 4.5 is still satisfied here.
The symmetry condition of Theorem 5.1 means that the matrix shape of
![]() ${\mathfrak n}\subset {\mathfrak {sl}}_{n+1}$
must be “almost” symmetric w.r.t. the antidiagonal. That is, the symmetry may only fail in case (b) for roots in
${\mathfrak n}\subset {\mathfrak {sl}}_{n+1}$
must be “almost” symmetric w.r.t. the antidiagonal. That is, the symmetry may only fail in case (b) for roots in
![]() $\Delta ({\mathfrak h}_s)$
with
$\Delta ({\mathfrak h}_s)$
with
![]() $i_{j-1}< s \leqslant i_j=k$
(if
$i_{j-1}< s \leqslant i_j=k$
(if ![]() , but
, but ![]() ).
).
Remark 5.2 Using Theorem 5.1, one easily computes the number of nontrivial (standard) nilradicals with generic stabilizers. For
![]() ${\mathsf {\mathbf {{A}}}}_{2n-1}$
, it is
${\mathsf {\mathbf {{A}}}}_{2n-1}$
, it is
![]() $2^{n+1}-3$
; for
$2^{n+1}-3$
; for
![]() ${\mathsf {\mathbf {{A}}}}_{2n}$
, it is
${\mathsf {\mathbf {{A}}}}_{2n}$
, it is
![]() $3(2^{n}-1)$
. Hence, the ratio
$3(2^{n}-1)$
. Hence, the ratio
![]() $\#\{\text {nilradicals with generic stabilizer}\}/\#\{\text {all nilradicals}\}$
exponentially decreases.
$\#\{\text {nilradicals with generic stabilizer}\}/\#\{\text {all nilradicals}\}$
exponentially decreases.
Theorem 5.3 If
![]() ${\mathfrak g}={\mathfrak {sp}}_{2n}$
, then a generic stabilizer exists for every nilradical
${\mathfrak g}={\mathfrak {sp}}_{2n}$
, then a generic stabilizer exists for every nilradical
![]() ${\mathfrak n}$
.
${\mathfrak n}$
.
Proof For an appropriate choice of a skew-symmetric bilinear form defining
![]() ${\mathfrak {sp}}_{2n}\subset {\mathfrak {sl}}_{2n}$
, a Borel subalgebra of
${\mathfrak {sp}}_{2n}\subset {\mathfrak {sl}}_{2n}$
, a Borel subalgebra of
![]() ${\mathfrak {sp}}_{2n}$
,
${\mathfrak {sp}}_{2n}$
,
![]() ${\mathfrak b}({\mathfrak {sp}}_{2n})$
, is the set of symplectic upper-triangular matrices (see Example 2.6). Then the matrix shape of any (standard) nilradical in
${\mathfrak b}({\mathfrak {sp}}_{2n})$
, is the set of symplectic upper-triangular matrices (see Example 2.6). Then the matrix shape of any (standard) nilradical in
![]() ${\mathfrak {sp}}_{2n}$
is symmetric w.r.t. the antidiagonal, and the approach in the proof of 3
${\mathfrak {sp}}_{2n}$
is symmetric w.r.t. the antidiagonal, and the approach in the proof of 3
![]() $^o$
(a) in Theorem 5.1 applies to any nilradical in
$^o$
(a) in Theorem 5.1 applies to any nilradical in
![]() ${\mathfrak {sp}}_{2n}$
. If
${\mathfrak {sp}}_{2n}$
. If ![]() and
and ![]() , where
, where
![]() $i_1<i_2<\dots < i_j=k$
, then
$i_1<i_2<\dots < i_j=k$
, then
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
belongs to the north-east
${\mathfrak n}^{\boldsymbol {\zeta }}$
belongs to the north-east
![]() $k\times k$
square in the abelian nilradical
$k\times k$
square in the abelian nilradical
![]() ${\mathfrak n}_{\{\alpha _{n}\}}$
. Here, the blocks
${\mathfrak n}_{\{\alpha _{n}\}}$
. Here, the blocks
![]() $\Gamma _j$
inside this square represent matrices that are symmetric w.r.t. the antidiagonal (cf. Figure 1a).
$\Gamma _j$
inside this square represent matrices that are symmetric w.r.t. the antidiagonal (cf. Figure 1a).
For these two series, we explicitly describe
![]() ${\mathcal F}({\mathfrak n})$
for any
${\mathcal F}({\mathfrak n})$
for any
![]() ${\mathfrak n}$
. This also demonstrates the role of commutative polarizations.
${\mathfrak n}$
. This also demonstrates the role of commutative polarizations.
5.1 The Frobenius semiradical
 ${\mathcal F}({\mathfrak n})$
for
${\mathcal F}({\mathfrak n})$
for
 ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
Let ![]() be a nilradical such that
be a nilradical such that ![]() . Then
. Then ![]() ,
, ![]() , and
, and ![]() . We may assume that
. We may assume that ![]() and then, as in the proof of Theorem 5.1, there are two possibilities.
and then, as in the proof of Theorem 5.1, there are two possibilities.
(a) ![]() . Then
. Then
![]() ${\mathfrak n}_{\{\alpha _k\}}$
and
${\mathfrak n}_{\{\alpha _k\}}$
and
![]() ${\mathfrak n}_{\{\alpha _{n+1-k}\}}$
are CP-ideals of
${\mathfrak n}_{\{\alpha _{n+1-k}\}}$
are CP-ideals of
![]() ${\mathfrak n}$
[Reference Panyushev22, Example 3.8], and hence
${\mathfrak n}$
[Reference Panyushev22, Example 3.8], and hence
![]() ${\mathcal F}({\mathfrak n})\subset {\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
(cf. Section 3.4(3)). Here,
${\mathcal F}({\mathfrak n})\subset {\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
(cf. Section 3.4(3)). Here,
![]() ${\mathfrak s}:={\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
is the north-east square of size k in
${\mathfrak s}:={\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
is the north-east square of size k in
![]() ${\mathfrak {sl}}_{n+1}$
. On the other hand,
${\mathfrak {sl}}_{n+1}$
. On the other hand,
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak s}$
(see Theorem 5.1) and
${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak s}$
(see Theorem 5.1) and
![]() ${\mathfrak b}{\cdot }{\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak s}$
. Hence,
${\mathfrak b}{\cdot }{\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak s}$
. Hence,
![]() ${\mathcal F}({\mathfrak n})={\mathfrak s}$
and
${\mathcal F}({\mathfrak n})={\mathfrak s}$
and
![]() $\dim {\mathcal F}({\mathfrak n})=k^2$
(see Figure 2). For the special case of
$\dim {\mathcal F}({\mathfrak n})=k^2$
(see Figure 2). For the special case of
![]() ${\mathfrak n}={\mathfrak u}$
, the description of
${\mathfrak n}={\mathfrak u}$
, the description of
![]() ${\mathcal F}({\mathfrak u})$
is obtained in [Reference Ooms19, Theorem 4.1].
${\mathcal F}({\mathfrak u})$
is obtained in [Reference Ooms19, Theorem 4.1].
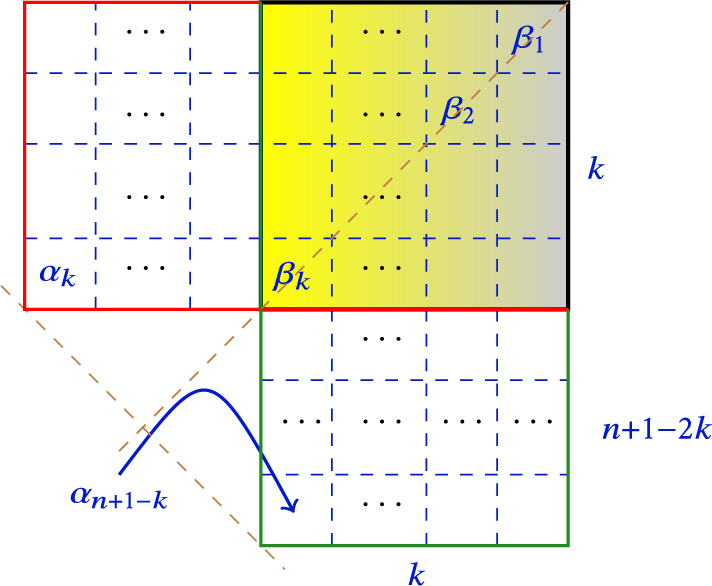
Figure 2:
![]() ${\mathcal F}({\mathfrak n})={\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
,
${\mathcal F}({\mathfrak n})={\mathfrak n}_{\{\alpha _k\}}\cap {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
,
![]() ${\mathfrak n}\supset {\mathfrak n}_{\{\alpha _k\}}\cup {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
.
${\mathfrak n}\supset {\mathfrak n}_{\{\alpha _k\}}\cup {\mathfrak n}_{\{\alpha _{n+1-k}\}}$
.
Actually, here,
![]() ${\mathfrak a}_j:={\mathfrak n}_{\{\alpha _j\}}\cap {\mathfrak n}$
is a CP-ideal of
${\mathfrak a}_j:={\mathfrak n}_{\{\alpha _j\}}\cap {\mathfrak n}$
is a CP-ideal of
![]() ${\mathfrak n}$
for any j such that
${\mathfrak n}$
for any j such that
![]() $k\leqslant j\leqslant n+1-k$
(see Example 4.8 in [Reference Panyushev22]).
$k\leqslant j\leqslant n+1-k$
(see Example 4.8 in [Reference Panyushev22]).
(b) ![]() . Then only
. Then only
![]() ${\mathfrak n}_{\{\alpha _k\}}$
is a CP-ideal and
${\mathfrak n}_{\{\alpha _k\}}$
is a CP-ideal and
![]() ${\mathcal F}({\mathfrak n})\subset {\mathfrak n}_{\{\alpha _k\}}$
. On the other hand,
${\mathcal F}({\mathfrak n})\subset {\mathfrak n}_{\{\alpha _k\}}$
. On the other hand,
![]() ${\mathsf {supp}}(\beta _k-\alpha _k)=\{\alpha _{k+1},\dots ,\alpha _{n+1-k}\}$
. Hence,
${\mathsf {supp}}(\beta _k-\alpha _k)=\{\alpha _{k+1},\dots ,\alpha _{n+1-k}\}$
. Hence,
![]() $\beta _k-\alpha _k\not \in \Delta ({\mathfrak n})$
and
$\beta _k-\alpha _k\not \in \Delta ({\mathfrak n})$
and
![]() $\alpha _k\in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
(see Theorem 4.4
(ii)). By Proposition 4.1
(i), this implies that
$\alpha _k\in \Delta ({\mathfrak n}^{\boldsymbol {\zeta }})$
(see Theorem 4.4
(ii)). By Proposition 4.1
(i), this implies that
![]() ${\mathfrak n}_{\{\alpha _k\}}\subset {\mathcal F}({\mathfrak n})$
. Thus, here,
${\mathfrak n}_{\{\alpha _k\}}\subset {\mathcal F}({\mathfrak n})$
. Thus, here,
![]() ${\mathcal F}({\mathfrak n})={\mathfrak n}_{\{\alpha _k\}}$
and
${\mathcal F}({\mathfrak n})={\mathfrak n}_{\{\alpha _k\}}$
and
![]() $\dim {\mathcal F}({\mathfrak n})=k(n+1-k)$
. Since
$\dim {\mathcal F}({\mathfrak n})=k(n+1-k)$
. Since
![]() ${\mathcal F}({\mathfrak n})$
appears to be a CP, we conclude that
${\mathcal F}({\mathfrak n})$
appears to be a CP, we conclude that
![]() ${\mathfrak n}_{\{\alpha _k\}}$
is the only CP for
${\mathfrak n}_{\{\alpha _k\}}$
is the only CP for
![]() ${\mathfrak n}$
.
${\mathfrak n}$
.
It follows from the descriptions above that for
![]() ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
,
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
,
![]() ${\mathcal F}({\mathfrak n})$
is always equal to the intersection of all CP-ideals of
${\mathcal F}({\mathfrak n})$
is always equal to the intersection of all CP-ideals of
![]() ${\mathfrak n}$
. But this is not true for other simple Lie algebras.
${\mathfrak n}$
. But this is not true for other simple Lie algebras.
5.2 The Frobenius semiradical
 ${\mathcal F}({\mathfrak n})$
for
${\mathcal F}({\mathfrak n})$
for
 ${\mathfrak g}={\mathfrak {sp}}_{2n}$
${\mathfrak g}={\mathfrak {sp}}_{2n}$
Let ![]() be a nilradical such that
be a nilradical such that ![]() . Then
. Then ![]() ,
, ![]() and
and ![]() . The abelian nilradical
. The abelian nilradical
![]() ${\mathfrak n}_{\{\alpha _{n}\}}$
is identified with the space of
${\mathfrak n}_{\{\alpha _{n}\}}$
is identified with the space of
![]() $n\times n$
matrices that are symmetric w.r.t. the antidiagonal (see Example 2.6). Then
$n\times n$
matrices that are symmetric w.r.t. the antidiagonal (see Example 2.6). Then
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
belongs to the north-east
${\mathfrak n}^{\boldsymbol {\zeta }}$
belongs to the north-east
![]() $k\times k$
square in
$k\times k$
square in
![]() ${\mathfrak n}_{\{\alpha _{n}\}}$
, and the south-west corner of this square,
${\mathfrak n}_{\{\alpha _{n}\}}$
, and the south-west corner of this square,
![]() ${\mathfrak g}_{\beta _k}$
, lies in
${\mathfrak g}_{\beta _k}$
, lies in
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
. Hence,
${\mathfrak n}^{\boldsymbol {\zeta }}$
. Hence,
![]() ${\mathcal F}({\mathfrak n})={\mathfrak b}{\cdot }{\mathfrak n}^{\boldsymbol {\zeta }}$
is equal to this k-square and
${\mathcal F}({\mathfrak n})={\mathfrak b}{\cdot }{\mathfrak n}^{\boldsymbol {\zeta }}$
is equal to this k-square and
![]() $\dim {\mathcal F}({\mathfrak n})=k(k+1)/2$
. In this case,
$\dim {\mathcal F}({\mathfrak n})=k(k+1)/2$
. In this case,
![]() ${\mathfrak a}:={\mathfrak n}_{\{\alpha _n\}}\cap {\mathfrak n}$
is the only CP-ideal of
${\mathfrak a}:={\mathfrak n}_{\{\alpha _n\}}\cap {\mathfrak n}$
is the only CP-ideal of
![]() ${\mathfrak n}$
and the inclusion
${\mathfrak n}$
and the inclusion
![]() ${\mathcal F}({\mathfrak n})\subset {\mathfrak a}$
is proper unless
${\mathcal F}({\mathfrak n})\subset {\mathfrak a}$
is proper unless
![]() $k=n$
(see the following picture).
$k=n$
(see the following picture).

Remark 5.4 The series
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
and
${\mathsf {\mathbf {{A}}}}_{n}$
and
![]() ${\mathsf {\mathbf {{C}}}}_{n}$
are easily handled, because
${\mathsf {\mathbf {{C}}}}_{n}$
are easily handled, because ![]() is a chain for them and any nilradical has a CP. Therefore,
is a chain for them and any nilradical has a CP. Therefore,
![]() ${\mathcal F}({\mathfrak n})$
is an abelian ideal of
${\mathcal F}({\mathfrak n})$
is an abelian ideal of
![]() ${\mathfrak n}$
, and there is a natural upper bound on
${\mathfrak n}$
, and there is a natural upper bound on
![]() ${\mathcal F}({\mathfrak n})$
. However, it can happen that
${\mathcal F}({\mathfrak n})$
. However, it can happen that
![]() ${\mathfrak n}$
does not have a CP, but
${\mathfrak n}$
does not have a CP, but
![]() ${\mathcal F}({\mathfrak n})$
is abelian (see Example 7.3).
${\mathcal F}({\mathfrak n})$
is abelian (see Example 7.3).
6 The Poisson center and U-invariants
Recall that
![]() $P=L{\cdot }N$
is a standard parabolic subgroup of G and
$P=L{\cdot }N$
is a standard parabolic subgroup of G and
![]() ${\mathfrak p}={\mathfrak l}\oplus {\mathfrak n}$
. Since N is connected, one has
${\mathfrak p}={\mathfrak l}\oplus {\mathfrak n}$
. Since N is connected, one has ![]() , and this algebra is the center of the Poisson algebra
, and this algebra is the center of the Poisson algebra ![]() . Because
. Because
![]() ${\mathfrak n}$
is a P-module, one can consider algebras of invariants in
${\mathfrak n}$
is a P-module, one can consider algebras of invariants in ![]() for any subgroup
for any subgroup
![]() $Q\subset P$
. Specifically, we are interested in the groups U and
$Q\subset P$
. Specifically, we are interested in the groups U and
![]() $\tilde N$
, where
$\tilde N$
, where
![]() ${\mathrm {Lie\,}} \tilde N=\tilde {\mathfrak n}$
is the optimization of
${\mathrm {Lie\,}} \tilde N=\tilde {\mathfrak n}$
is the optimization of
![]() ${\mathfrak n}$
. We also wish to compare the algebras of Q-invariants in
${\mathfrak n}$
. We also wish to compare the algebras of Q-invariants in ![]() and
and ![]() . The algebras of interest for us are organized in the following diagram:
. The algebras of interest for us are organized in the following diagram:

If an algebra ![]() is finitely generated, then we also consider the associated quotient morphism
is finitely generated, then we also consider the associated quotient morphism
![]() $\pi _Q: {\mathfrak n}^{*}\to {\mathfrak n}^{*}/\!\!/ Q:={\mathsf {Spec\,}}({\mathbb C}[{\mathfrak n}^{*}]^Q)$
.
$\pi _Q: {\mathfrak n}^{*}\to {\mathfrak n}^{*}/\!\!/ Q:={\mathsf {Spec\,}}({\mathbb C}[{\mathfrak n}^{*}]^Q)$
.
For any nilradical
![]() ${\mathfrak n}$
, one can form the solvable Lie algebra
${\mathfrak n}$
, one can form the solvable Lie algebra
where ![]() . By [Reference Panyushev22, Proposition 5.1], the corresponding connected group
. By [Reference Panyushev22, Proposition 5.1], the corresponding connected group
![]() $F_{\mathfrak n}\subset B$
has an open orbit in
$F_{\mathfrak n}\subset B$
has an open orbit in
![]() ${\mathfrak f}_{\mathfrak n}^{*}$
, i.e.,
${\mathfrak f}_{\mathfrak n}^{*}$
, i.e.,
![]() ${\mathfrak f}_n$
is a Frobenius Lie algebra. For this reason,
${\mathfrak f}_n$
is a Frobenius Lie algebra. For this reason,
![]() ${\mathfrak f}_{\mathfrak n}$
is called the Frobenius envelope of
${\mathfrak f}_{\mathfrak n}$
is called the Frobenius envelope of
![]() ${\mathfrak n}$
. Note that the unipotent radical of
${\mathfrak n}$
. Note that the unipotent radical of
![]() $F_{\mathfrak n}$
is
$F_{\mathfrak n}$
is
![]() $\tilde N$
.
$\tilde N$
.
Lemma 6.1 The four algebras of invariants forming the square in (6.1) are polynomial. In particular, for any optimal nilradical
![]() $\tilde {\mathfrak n}$
, the Poisson center
$\tilde {\mathfrak n}$
, the Poisson center ![]() is polynomial.
is polynomial.
Proof
1
![]() $^o$
. For any nilradical
$^o$
. For any nilradical
![]() ${\mathfrak n}$
, the action
${\mathfrak n}$
, the action
![]() $(B:{\mathfrak n}^{*})$
is locally transitive and
$(B:{\mathfrak n}^{*})$
is locally transitive and
![]() $B{\cdot }{\boldsymbol {\zeta }}$
is the dense orbit in
$B{\cdot }{\boldsymbol {\zeta }}$
is the dense orbit in
![]() ${\mathfrak n}^{*}$
[Reference Joseph12, 2.4]. Therefore,
${\mathfrak n}^{*}$
[Reference Joseph12, 2.4]. Therefore, ![]() is a polynomial algebra and
is a polynomial algebra and ![]() equals the number of prime divisors in
equals the number of prime divisors in
![]() ${\mathfrak n}^{*}\setminus B{\cdot }{\boldsymbol {\zeta }}$
(see [Reference Panyushev21, Theorem 4.4]). Hence, the algebras in the first column of (6.1) are polynomial.
${\mathfrak n}^{*}\setminus B{\cdot }{\boldsymbol {\zeta }}$
(see [Reference Panyushev21, Theorem 4.4]). Hence, the algebras in the first column of (6.1) are polynomial.
2
![]() $^o$
. More generally, the
$^o$
. More generally, the
![]() $F_{\mathfrak n}$
-equivariant embeddings
$F_{\mathfrak n}$
-equivariant embeddings
![]() ${\mathfrak n}\hookrightarrow \tilde {\mathfrak n}\hookrightarrow {\mathfrak f}_{\mathfrak n}$
yield the
${\mathfrak n}\hookrightarrow \tilde {\mathfrak n}\hookrightarrow {\mathfrak f}_{\mathfrak n}$
yield the
![]() $F_{\mathfrak n}$
-equivariant projections
$F_{\mathfrak n}$
-equivariant projections
![]() ${\mathfrak f}_{\mathfrak n}^{*}\to \tilde {\mathfrak n}^{*}\to {\mathfrak n}^{*}$
, which implies that
${\mathfrak f}_{\mathfrak n}^{*}\to \tilde {\mathfrak n}^{*}\to {\mathfrak n}^{*}$
, which implies that
![]() $F_{\mathfrak n}$
has a dense orbit in
$F_{\mathfrak n}$
has a dense orbit in
![]() ${\mathfrak n}^{*}$
, too. Therefore, arguing as in [Reference Panyushev21, Section 4], one proves that
${\mathfrak n}^{*}$
, too. Therefore, arguing as in [Reference Panyushev21, Section 4], one proves that ![]() is also a polynomial algebra. Thus, the algebras in the second column of (6.1) are polynomial, too.
is also a polynomial algebra. Thus, the algebras in the second column of (6.1) are polynomial, too.
If
![]() ${\mathfrak n}\ne \tilde {\mathfrak n}$
, then the Poisson center
${\mathfrak n}\ne \tilde {\mathfrak n}$
, then the Poisson center ![]() is not always polynomial (see examples below).
is not always polynomial (see examples below).
Lemma 6.2 For any nilradical
![]() ${\mathfrak n}$
, we have
${\mathfrak n}$
, we have ![]() .
.
Proof It is clear that ![]() . On the other hand, by [Reference Panyushev22, Proposition 5.5], the equality
. On the other hand, by [Reference Panyushev22, Proposition 5.5], the equality
![]() $\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})$
(see Proposition 2.3) implies that
$\boldsymbol {b}({\mathfrak n})=\boldsymbol {b}(\tilde {\mathfrak n})$
(see Proposition 2.3) implies that ![]() . Hence,
. Hence, ![]() .
.
Lemma 6.3 For any nilradical
![]() ${\mathfrak n}$
, we have
${\mathfrak n}$
, we have ![]() .
.
Proof
1
![]() $^o$
. Let us first prove that
$^o$
. Let us first prove that ![]() . Since
. Since
![]() $\tilde N$
is unipotent, the field of invariants
$\tilde N$
is unipotent, the field of invariants
![]() ${\mathbb C}({\mathfrak n}^{*})^{\tilde N}$
is the quotient field of the algebra of invariants
${\mathbb C}({\mathfrak n}^{*})^{\tilde N}$
is the quotient field of the algebra of invariants ![]() [Reference Brion4, Chapter 1.4]. Furthermore, by Rosenlicht’s theorem [Reference Brion4, Chapter 1.6], one has
[Reference Brion4, Chapter 1.4]. Furthermore, by Rosenlicht’s theorem [Reference Brion4, Chapter 1.6], one has
and the same holds for U in place of
![]() $\tilde N$
. Therefore, since
$\tilde N$
. Therefore, since
it suffices to prove that one has equality here. By Theorem 4.7,
![]() $\tilde N{\cdot }{\mathfrak k}$
is dense in
$\tilde N{\cdot }{\mathfrak k}$
is dense in
![]() ${\mathfrak n}^{*}$
. Hence,
${\mathfrak n}^{*}$
. Hence,
![]() $U{\cdot }{\mathfrak k}$
is dense in
$U{\cdot }{\mathfrak k}$
is dense in
![]() ${\mathfrak n}^{*}$
, too.
${\mathfrak n}^{*}$
, too.
Now,
![]() ${\mathfrak u}=({\mathfrak u}\cap \tilde {\mathfrak l})\oplus \tilde {\mathfrak n}$
, where
${\mathfrak u}=({\mathfrak u}\cap \tilde {\mathfrak l})\oplus \tilde {\mathfrak n}$
, where
![]() $\tilde {\mathfrak l}$
is the standard Levi subalgebra of
$\tilde {\mathfrak l}$
is the standard Levi subalgebra of
![]() $\tilde {\mathfrak p}:=\mathsf {norm}_{\mathfrak g}(\tilde {\mathfrak n})$
. Since
$\tilde {\mathfrak p}:=\mathsf {norm}_{\mathfrak g}(\tilde {\mathfrak n})$
. Since
![]() $\tilde {\mathfrak n}$
is optimal,
$\tilde {\mathfrak n}$
is optimal,
![]() ${\mathfrak u}\cap \tilde {\mathfrak l}$
stabilizes any
${\mathfrak u}\cap \tilde {\mathfrak l}$
stabilizes any
![]() $\xi \in {\mathfrak k}_0\subset {\mathfrak k}$
. Hence,
$\xi \in {\mathfrak k}_0\subset {\mathfrak k}$
. Hence,
![]() ${\mathfrak u}^{\xi }=({\mathfrak u}\cap \tilde {\mathfrak l})\oplus \tilde {\mathfrak n}^{\xi }$
and
${\mathfrak u}^{\xi }=({\mathfrak u}\cap \tilde {\mathfrak l})\oplus \tilde {\mathfrak n}^{\xi }$
and
![]() $\dim U{\cdot }\xi =\dim \tilde N{\cdot }\xi $
. Therefore,
$\dim U{\cdot }\xi =\dim \tilde N{\cdot }\xi $
. Therefore,
![]() $\max _{\xi \in {\mathfrak n}^{*}}\dim U{\cdot }\xi = \max _{\xi \in {\mathfrak n}^{*}}\dim \tilde N{\cdot }\xi $
, and we are done.
$\max _{\xi \in {\mathfrak n}^{*}}\dim U{\cdot }\xi = \max _{\xi \in {\mathfrak n}^{*}}\dim \tilde N{\cdot }\xi $
, and we are done.
2
![]() $^o$
. By the first part, the extension
$^o$
. By the first part, the extension ![]() is algebraic. But the algebra of invariants of a connected algebraic group Q acting on an affine variety X is algebraically closed in
is algebraic. But the algebra of invariants of a connected algebraic group Q acting on an affine variety X is algebraically closed in
![]() ${\mathbb C}[X]$
(see [Reference Kraft14, p. 100]).
${\mathbb C}[X]$
(see [Reference Kraft14, p. 100]).
Combining previous lemmas yields our main result on diagram (6.1).
Theorem 6.4 The four algebras of invariants that form the square in (6.1) are equal, i.e.,
These algebras are polynomial, and their common transcendence degree is ![]() . If
. If
![]() ${\mathfrak n}\ne \tilde {\mathfrak n}$
, then
${\mathfrak n}\ne \tilde {\mathfrak n}$
, then ![]() . Thus, there are at most two different algebras of invariants in (6.1).
. Thus, there are at most two different algebras of invariants in (6.1).
Proof (1) By Lemma 6.1, these four algebras are polynomial.
(2) By Lemmas 6.2 and 6.3, these four algebras are equal. (Note that Lemma 6.3 applies also to
![]() $\tilde {\mathfrak n}$
in place of
$\tilde {\mathfrak n}$
in place of
![]() ${\mathfrak n}$
.)
${\mathfrak n}$
.)
(3) Since both
![]() $\tilde N$
and N are unipotent, it follows from the Rosenlicht theorem that
$\tilde N$
and N are unipotent, it follows from the Rosenlicht theorem that ![]() and
and ![]() . Hence, the last relation is just Eq. (4.1).
. Hence, the last relation is just Eq. (4.1).
Remark 6.5 The algebra of U-invariants in ![]() is polynomial for an arbitrary
is polynomial for an arbitrary
![]() ${\mathfrak b}$
-stable ideal
${\mathfrak b}$
-stable ideal
![]() ${\mathfrak r}$
of
${\mathfrak r}$
of
![]() ${\mathfrak u}$
. That is, if
${\mathfrak u}$
. That is, if
![]() ${\mathfrak r}\subset {\mathfrak u}$
and
${\mathfrak r}\subset {\mathfrak u}$
and
![]() $[{\mathfrak b},{\mathfrak r}]\subset {\mathfrak r}$
, then
$[{\mathfrak b},{\mathfrak r}]\subset {\mathfrak r}$
, then ![]() is a polynomial algebra. The reason is that B has an open orbit in
is a polynomial algebra. The reason is that B has an open orbit in
![]() ${\mathfrak r}^{*}$
(see [Reference Panyushev21, Section 4] for details).
${\mathfrak r}^{*}$
(see [Reference Panyushev21, Section 4] for details).
Corollary 6.6 For any nilradical
![]() ${\mathfrak n}$
and a cascade point
${\mathfrak n}$
and a cascade point
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}_0\subset {\mathfrak n}^{*}$
, we have:
${\boldsymbol {\zeta }}\in {\mathfrak k}_0\subset {\mathfrak n}^{*}$
, we have:
-
(1)
 ;
; -
(2)
 $B{\cdot }{\boldsymbol {\zeta }}=F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
.
$B{\cdot }{\boldsymbol {\zeta }}=F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
.
Proof (1) It is known that:
-
•
 ;
; -
•
 [Reference Panyushev21, Theorem 4.4];
[Reference Panyushev21, Theorem 4.4]; -
•
 .
.
The last equality relies on the facts that the orbit
![]() $F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
is open in
$F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
is open in
![]() ${\mathfrak n}^{*}$
and
${\mathfrak n}^{*}$
and
![]() $\tilde N$
is the unipotent radical of
$\tilde N$
is the unipotent radical of
![]() $F_{\mathfrak n}$
. Hence, [Reference Panyushev21, Theorem 4.4] applies also in this case.
$F_{\mathfrak n}$
. Hence, [Reference Panyushev21, Theorem 4.4] applies also in this case.
(2) Since B and
![]() $F_{\mathfrak n}$
are solvable, the orbits
$F_{\mathfrak n}$
are solvable, the orbits
![]() $B{\cdot }{\boldsymbol {\zeta }}$
and
$B{\cdot }{\boldsymbol {\zeta }}$
and
![]() $F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
are affine. Therefore, both
$F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
are affine. Therefore, both
![]() ${\mathfrak n}^{*}\setminus B{\cdot }{\boldsymbol {\zeta }}$
and
${\mathfrak n}^{*}\setminus B{\cdot }{\boldsymbol {\zeta }}$
and
![]() ${\mathfrak n}^{*}\setminus F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
are the union of divisors and the assertion follows from (1).
${\mathfrak n}^{*}\setminus F_{\mathfrak n}{\cdot }{\boldsymbol {\zeta }}$
are the union of divisors and the assertion follows from (1).
If
![]() ${\mathfrak n}$
is not optimal, then
${\mathfrak n}$
is not optimal, then ![]() is not always polynomial (see Example 6.10). Actually, there are Lie algebras
is not always polynomial (see Example 6.10). Actually, there are Lie algebras
![]() ${\mathfrak q}$
such that
${\mathfrak q}$
such that ![]() is not finitely generated! A construction of such
is not finitely generated! A construction of such
![]() ${\mathfrak q}$
utilizing the Nagata counterexample to Hilbert’s 14th problem is given by Dixmier in [Reference Dixmier5, 4.9.20(c)]. Nevertheless, we demonstrate below that, for the nilradicals in
${\mathfrak q}$
utilizing the Nagata counterexample to Hilbert’s 14th problem is given by Dixmier in [Reference Dixmier5, 4.9.20(c)]. Nevertheless, we demonstrate below that, for the nilradicals in
![]() ${\mathfrak g}$
, the algebra
${\mathfrak g}$
, the algebra ![]() is as good as the algebras of invariants of linear actions of reductive groups. Recall that a commutative associative
is as good as the algebras of invariants of linear actions of reductive groups. Recall that a commutative associative
![]() ${\mathbb C}$
-algebra
${\mathbb C}$
-algebra
![]() ${\mathcal A}$
equipped with action of an algebraic group Q is called a rational Q-algebra if, for any
${\mathcal A}$
equipped with action of an algebraic group Q is called a rational Q-algebra if, for any
![]() $a\in {\mathcal A}$
, the linear span in
$a\in {\mathcal A}$
, the linear span in
![]() ${\mathcal A}$
of the orbit
${\mathcal A}$
of the orbit
![]() $Q{\cdot }a$
is finite-dimensional and the representation of Q on
$Q{\cdot }a$
is finite-dimensional and the representation of Q on
![]() $\langle Q{\cdot }a\rangle $
is rational (see, e.g., [Reference Grosshans11, p.1]).
$\langle Q{\cdot }a\rangle $
is rational (see, e.g., [Reference Grosshans11, p.1]).
Theorem 6.7 Let
![]() ${\mathfrak n}$
be an arbitrary nilradical in
${\mathfrak n}$
be an arbitrary nilradical in
![]() ${\mathfrak g}$
. Then:
${\mathfrak g}$
. Then:
-
(i) the algebra
 is finitely generated;
is finitely generated; -
(ii) the quotient variety
 ${\mathfrak n}^{*}/\!\!/ N$
has rational singularities.
${\mathfrak n}^{*}/\!\!/ N$
has rational singularities.
Proof
(i) Let
![]() ${\mathfrak p}$
be the parabolic subalgebra with
${\mathfrak p}$
be the parabolic subalgebra with
![]() ${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
. Let
${\mathfrak n}={\mathfrak p}^{\mathsf {nil}}$
. Let
![]() ${\mathfrak l}$
be the standard Levi subalgebra of
${\mathfrak l}$
be the standard Levi subalgebra of
![]() ${\mathfrak p}$
and L the corresponding Levi subgroup of
${\mathfrak p}$
and L the corresponding Levi subgroup of
![]() $P=\mathsf {Norm}_G({\mathfrak n})\subset G$
. Since
$P=\mathsf {Norm}_G({\mathfrak n})\subset G$
. Since
![]() $[{\mathfrak l},{\mathfrak n}]\subset {\mathfrak n}$
, the algebra
$[{\mathfrak l},{\mathfrak n}]\subset {\mathfrak n}$
, the algebra ![]() is a rational L-algebra. Set
is a rational L-algebra. Set
![]() $U(L)=U\cap L$
. It is a maximal unipotent subgroup of L, and U is a semi-direct product of
$U(L)=U\cap L$
. It is a maximal unipotent subgroup of L, and U is a semi-direct product of
![]() $U(L)$
and N. By Theorem 6.4,
$U(L)$
and N. By Theorem 6.4, ![]() is a polynomial algebra. Now, we can apply Corollary 4 from [Reference Popov23, Section 3], which asserts that if
is a polynomial algebra. Now, we can apply Corollary 4 from [Reference Popov23, Section 3], which asserts that if
![]() ${\mathcal A}$
is a rational L-algebra, then
${\mathcal A}$
is a rational L-algebra, then
![]() ${\mathcal A}$
is finitely generated if and only if
${\mathcal A}$
is finitely generated if and only if
![]() ${\mathcal A}^{U(L)}$
is. In our case,
${\mathcal A}^{U(L)}$
is. In our case, ![]() and
and
![]() ${\mathcal A}^{U(L)}$
is a polynomial algebra, with
${\mathcal A}^{U(L)}$
is a polynomial algebra, with ![]() generators. Hence,
generators. Hence, ![]() is finitely generated.
is finitely generated.
(ii) Let
(P)
be a so-called “stable property” of local rings of algebraic varieties (see [Reference Popov23, Section 6] for the details). By [Reference Popov23, Theorem 6],
![]() ${\mathcal A}$
has property
(P)
if and only if
${\mathcal A}$
has property
(P)
if and only if
![]() ${\mathcal A}^{U(L)}$
has. Since rationality of singularities is such a property, we obtain the second assertion.
${\mathcal A}^{U(L)}$
has. Since rationality of singularities is such a property, we obtain the second assertion.
Remark 6.8 (1) Part (i) of Theorem 6.7 appears in [Reference Joseph12, Lemma 4.6(ii)], with another proof. Namely, in place of reference to [Reference Popov23], one can provide the following simple argument for the implication:
Let
![]() $f_1,\dots ,f_l$
be a set of generators for
$f_1,\dots ,f_l$
be a set of generators for
![]() ${\mathcal A}^{U(L)}$
. We may also assume that each
${\mathcal A}^{U(L)}$
. We may also assume that each
![]() $f_i$
is a T-eigenvector. Then the
$f_i$
is a T-eigenvector. Then the
![]() ${\mathbb C}$
-linear span of
${\mathbb C}$
-linear span of
![]() $L{\cdot }f_i\subset {\mathcal A}$
is a simple finite-dimensional L-module, say
$L{\cdot }f_i\subset {\mathcal A}$
is a simple finite-dimensional L-module, say
![]() $\mathsf {V}_i$
. It is easily seen that the
$\mathsf {V}_i$
. It is easily seen that the
![]() ${\mathbb C}$
-algebra generated by
${\mathbb C}$
-algebra generated by
![]() $\sum _{i=1}^l \mathsf {V}_i$
is L-stable and contains all simple L-modules from
$\sum _{i=1}^l \mathsf {V}_i$
is L-stable and contains all simple L-modules from
![]() ${\mathcal A}$
. Hence, the finite-dimensional space
${\mathcal A}$
. Hence, the finite-dimensional space
![]() $\sum _{i=1}^l \mathsf {V}_i$
generates
$\sum _{i=1}^l \mathsf {V}_i$
generates
![]() ${\mathcal A}$
.
${\mathcal A}$
.
(2) There is also an alternate approach to part (ii). By a result of Kostant, the algebra
![]() ${\mathbb C}[{\mathfrak n}^{*}]^N$
is a multiplicity free L-module (see [Reference Joseph12, 4.5]). Being the algebra of invariants of a linear action,
${\mathbb C}[{\mathfrak n}^{*}]^N$
is a multiplicity free L-module (see [Reference Joseph12, 4.5]). Being the algebra of invariants of a linear action,
![]() ${\mathbb C}[{\mathfrak n}^{*}]^N$
is also integrally closed. Therefore,
${\mathbb C}[{\mathfrak n}^{*}]^N$
is also integrally closed. Therefore,
![]() ${\mathfrak n}^{*}/\!\!/ N$
is a spherical L-variety. By [Reference Popov23, Theorem 10], this implies that
${\mathfrak n}^{*}/\!\!/ N$
is a spherical L-variety. By [Reference Popov23, Theorem 10], this implies that
![]() ${\mathfrak n}^{*}/\!\!/ N$
has rational singularities.
${\mathfrak n}^{*}/\!\!/ N$
has rational singularities.
Remark 6.9
(1) The general treatment of “stable properties” is due to Popov [Reference Popov23], but the assertion that relates rationality of singularities for
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal A}^{U(L)}$
goes back to Kraft and Luna (see exposition in Brion’s thesis [Reference Brion2, Chapter I(c)]). It is worth noting that, for a rational L-algebra
${\mathcal A}^{U(L)}$
goes back to Kraft and Luna (see exposition in Brion’s thesis [Reference Brion2, Chapter I(c)]). It is worth noting that, for a rational L-algebra
![]() ${\mathcal A}$
, the equivalence
${\mathcal A}$
, the equivalence
holds over an algebraically closed field of an arbitrary characteristic (see [Reference Grosshans11, Theorem 16.2]).
(2) A list of “stable properties” is found in [Reference Popov23, Section 6].
Example 6.10
(1) Take
![]() ${\mathfrak g}=\mathfrak {sl}_5$
and
${\mathfrak g}=\mathfrak {sl}_5$
and ![]() with
with ![]() . Then
. Then
![]() $\dim {\mathfrak n}=7$
,
$\dim {\mathfrak n}=7$
, ![]() , and
, and
![]() $\tilde {\mathfrak n}={\mathfrak u}$
. Hence,
$\tilde {\mathfrak n}={\mathfrak u}$
. Hence,
![]() ${\mathrm {ind}}\,{\mathfrak n}=5$
. Let
${\mathrm {ind}}\,{\mathfrak n}=5$
. Let
![]() $\{e_{ij}\mid 1\leqslant i<j\leqslant 5, j=4,5\}$
be the matrix units corresponding to
$\{e_{ij}\mid 1\leqslant i<j\leqslant 5, j=4,5\}$
be the matrix units corresponding to
![]() ${\mathfrak n}$
(i.e., a basis for
${\mathfrak n}$
(i.e., a basis for
![]() ${\mathfrak n}$
). We regard them as (linear) functions on
${\mathfrak n}$
). We regard them as (linear) functions on
![]() ${\mathfrak n}^-\simeq {\mathfrak n}^{*}$
. Here,
${\mathfrak n}^-\simeq {\mathfrak n}^{*}$
. Here,
![]() $e_{15}\in {\mathfrak g}_{\beta _1}$
and
$e_{15}\in {\mathfrak g}_{\beta _1}$
and
![]() $e_{24}\in {\mathfrak g}_{\beta _2}$
. Obviously,
$e_{24}\in {\mathfrak g}_{\beta _2}$
. Obviously,
![]() $e_{15}$
and
$e_{15}$
and
 $f_{12}=\begin {vmatrix} e_{14} & e_{15} \\ e_{24} & e_{25} \end {vmatrix}$
belong to
$f_{12}=\begin {vmatrix} e_{14} & e_{15} \\ e_{24} & e_{25} \end {vmatrix}$
belong to ![]() . For the standard Levi subalgebra
. For the standard Levi subalgebra
![]() ${\mathfrak l}$
of
${\mathfrak l}$
of
![]() ${\mathfrak p}=\mathsf {norm}_{\mathfrak g}({\mathfrak n})$
, one has
${\mathfrak p}=\mathsf {norm}_{\mathfrak g}({\mathfrak n})$
, one has
![]() $[{\mathfrak l},{\mathfrak l}]={\mathfrak {sl}}_3$
; hence,
$[{\mathfrak l},{\mathfrak l}]={\mathfrak {sl}}_3$
; hence, ![]() is an
is an
![]() ${\mathfrak {sl}}_3$
-module. Taking the
${\mathfrak {sl}}_3$
-module. Taking the
![]() ${\mathfrak {sl}}_3$
-modules generated by
${\mathfrak {sl}}_3$
-modules generated by
![]() $e_{15}$
and
$e_{15}$
and
![]() $f_{12}$
, one obtains six functions that generate
$f_{12}$
, one obtains six functions that generate ![]() :
:
 $$\begin{align*}e_{15},e_{25},e_{35},f_{12}=\begin{vmatrix} e_{14} & e_{15} \\ e_{24} & e_{25} \end{vmatrix}, \ f_{13}= \begin{vmatrix} e_{14} & e_{15} \\ e_{34} & e_{35} \end{vmatrix}, \ f_{23}=\begin{vmatrix} e_{24} & e_{25} \\ e_{34} & e_{35} \end{vmatrix}. \end{align*}$$
$$\begin{align*}e_{15},e_{25},e_{35},f_{12}=\begin{vmatrix} e_{14} & e_{15} \\ e_{24} & e_{25} \end{vmatrix}, \ f_{13}= \begin{vmatrix} e_{14} & e_{15} \\ e_{34} & e_{35} \end{vmatrix}, \ f_{23}=\begin{vmatrix} e_{24} & e_{25} \\ e_{34} & e_{35} \end{vmatrix}. \end{align*}$$
Since
![]() $f_{12}\not \in {\mathbb C}[e_{15},e_{25},e_{35}]$
and a minimal generating system can be chosen to be
$f_{12}\not \in {\mathbb C}[e_{15},e_{25},e_{35}]$
and a minimal generating system can be chosen to be
![]() $SL_3$
-invariant, the set of generators above is minimal. These generators satisfy the relation
$SL_3$
-invariant, the set of generators above is minimal. These generators satisfy the relation
![]() $e_{15}f_{23}-e_{25}f_{13}+e_{35}f_{12}=0$
; hence,
$e_{15}f_{23}-e_{25}f_{13}+e_{35}f_{12}=0$
; hence,
![]() ${\mathfrak n}^{*}/\!\!/ N$
is a hypersurface. Under passage to
${\mathfrak n}^{*}/\!\!/ N$
is a hypersurface. Under passage to
![]() $\tilde N$
or U, the situation improves, because
$\tilde N$
or U, the situation improves, because ![]() .
.
(2) More generally, for
![]() ${\mathfrak g}=\mathfrak {sl}_N$
and
${\mathfrak g}=\mathfrak {sl}_N$
and ![]() with
with
![]() $k\leqslant N/2$
, one has
$k\leqslant N/2$
, one has
Here,
![]() $[{\mathfrak l},{\mathfrak l}]=\mathfrak {sl}_{N-k}$
and
$[{\mathfrak l},{\mathfrak l}]=\mathfrak {sl}_{N-k}$
and ![]() , where
, where
![]() $F_i$
is the “anti-principal” minor of degree i, i.e.,
$F_i$
is the “anti-principal” minor of degree i, i.e.,
 $$\begin{align*}F_1=e_{1,N}, \ F_2=\begin{vmatrix} e_{1,N-1} & e_{1,N} \\ e_{2,N-1} & e_{2,N} \end{vmatrix},\dots, F_k=\begin{vmatrix} e_{1,N-k+1} & \cdots & e_{1,N} \\ \cdots & \cdots & \cdots \\ e_{k,N-k+1} & \cdots & e_{k,N} \end{vmatrix}. \end{align*}$$
$$\begin{align*}F_1=e_{1,N}, \ F_2=\begin{vmatrix} e_{1,N-1} & e_{1,N} \\ e_{2,N-1} & e_{2,N} \end{vmatrix},\dots, F_k=\begin{vmatrix} e_{1,N-k+1} & \cdots & e_{1,N} \\ \cdots & \cdots & \cdots \\ e_{k,N-k+1} & \cdots & e_{k,N} \end{vmatrix}. \end{align*}$$
The
![]() $SL_{N{-}k}$
-module generated by
$SL_{N{-}k}$
-module generated by
![]() $F_i$
,
$F_i$
,
![]() $\langle SL_{N-k}{\cdot }F_i\rangle $
, is isomorphic to
$\langle SL_{N-k}{\cdot }F_i\rangle $
, is isomorphic to
![]() $\wedge ^i \mathbb V$
, where
$\wedge ^i \mathbb V$
, where
![]() $\mathbb V$
is the standard
$\mathbb V$
is the standard
![]() $SL_{N{-}k}$
-module. It is also easily seen that
$SL_{N{-}k}$
-module. It is also easily seen that
![]() $F_j$
does not belong to the
$F_j$
does not belong to the
![]() ${\mathbb C}$
-algebra generated by
${\mathbb C}$
-algebra generated by
![]() $\sum _{i=1}^{j-1}\langle SL_{N-k}{\cdot }F_i\rangle $
. Therefore, the minimal number of generators of
$\sum _{i=1}^{j-1}\langle SL_{N-k}{\cdot }F_i\rangle $
. Therefore, the minimal number of generators of ![]() is
is

If
![]() $k=1$
, then
$k=1$
, then ![]() is abelian and
is abelian and ![]() . If
. If
![]() $k\geqslant 2$
, then
$k\geqslant 2$
, then ![]() and the equality holds only for
and the equality holds only for
![]() $k=2, N=4$
.
$k=2, N=4$
.
(3) For
![]() ${\mathsf {\mathbf {{E}}}}_{6}$
and
${\mathsf {\mathbf {{E}}}}_{6}$
and ![]() , one has
, one has ![]() ,
, ![]() , and
, and ![]() . Here,
. Here,
![]() $[{\mathfrak l},{\mathfrak l}]= {\mathfrak {sl}}_2\oplus \mathfrak {sl}_{5}$
and
$[{\mathfrak l},{\mathfrak l}]= {\mathfrak {sl}}_2\oplus \mathfrak {sl}_{5}$
and ![]() , where
, where
![]() $\deg F_i=1,2,4$
for
$\deg F_i=1,2,4$
for
![]() $i=1,2,3$
, respectively. Using the
$i=1,2,3$
, respectively. Using the
![]() ${\mathfrak l}$
-modules generated by
${\mathfrak l}$
-modules generated by
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, one can prove that
$F_2$
, one can prove that ![]() .
.
7 On the square integrable nilradicals
Recall that any nilradical ![]() is equipped with the canonical
is equipped with the canonical
![]() ${\mathbb Z}$
-grading
${\mathbb Z}$
-grading ![]() , where
, where ![]() and
and ![]() is the center of
is the center of
![]() ${\mathfrak n}$
. Accordingly, one obtains the partition
${\mathfrak n}$
. Accordingly, one obtains the partition ![]() (see Section 2.3).
(see Section 2.3).
Clearly,
![]() ${\mathrm {ind}}\,{\mathfrak n}\geqslant \dim {\mathfrak z}({\mathfrak n})$
and
${\mathrm {ind}}\,{\mathfrak n}\geqslant \dim {\mathfrak z}({\mathfrak n})$
and ![]() . Following [Reference Elashvili9, Reference Elashvili and Ooms10], we say that
. Following [Reference Elashvili9, Reference Elashvili and Ooms10], we say that
![]() ${\mathfrak n}$
is square integrable, if
${\mathfrak n}$
is square integrable, if
![]() ${\mathrm {ind}}\,{\mathfrak n}=\dim {\mathfrak z}({\mathfrak n})$
. Then
${\mathrm {ind}}\,{\mathfrak n}=\dim {\mathfrak z}({\mathfrak n})$
. Then
![]() ${\mathfrak n}^{\xi }={\mathfrak z}({\mathfrak n})$
for any
${\mathfrak n}^{\xi }={\mathfrak z}({\mathfrak n})$
for any
![]() $\xi \in {\mathfrak n}^{*}_{\mathsf {reg}}$
and hence
$\xi \in {\mathfrak n}^{*}_{\mathsf {reg}}$
and hence
![]() ${\mathcal F}({\mathfrak n})={\mathfrak z}({\mathfrak n})$
is abelian. Since
${\mathcal F}({\mathfrak n})={\mathfrak z}({\mathfrak n})$
is abelian. Since ![]() , the extension
, the extension ![]() is algebraic. This implies that
is algebraic. This implies that ![]() and hence
and hence ![]() is a free
is a free ![]() -module. It is easily seen that a Heisenberg algebra
-module. It is easily seen that a Heisenberg algebra
![]() ${\mathfrak h}$
is square integrable, with
${\mathfrak h}$
is square integrable, with
![]() ${\mathrm {ind}}\,{\mathfrak h}=1$
. Using
${\mathrm {ind}}\,{\mathfrak h}=1$
. Using ![]() and our description of
and our description of
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
, we classify all square integrable nilradicals. Recall that
${\mathfrak n}^{\boldsymbol {\zeta }}$
, we classify all square integrable nilradicals. Recall that ![]() is a poset.
is a poset.
Lemma 7.1 For any ![]() , we have
, we have ![]() .
.
Proof Take ![]() and
and ![]() . Then there are the following possibilities:
. Then there are the following possibilities:
-
•
 $\beta =\alpha $
. Then
$\beta =\alpha $
. Then  .
. -
•
 $\beta \ne \alpha $
and
$\beta \ne \alpha $
and
 $\Phi (\beta )=\{ \alpha \}$
. Recall that
$\Phi (\beta )=\{ \alpha \}$
. Recall that
 $\beta $
is the highest root in the root system with basis
$\beta $
is the highest root in the root system with basis
 ${\mathsf {supp}}(\beta )$
. Since
${\mathsf {supp}}(\beta )$
. Since
 $\beta $
is a minimal element of
$\beta $
is a minimal element of  , we have
, we have  . Then
. Then
 $[\beta :\alpha ]=2$
and
$[\beta :\alpha ]=2$
and  .
. -
•
 $\Phi (\beta )=\{\alpha ,\alpha '\}$
. Here,
$\Phi (\beta )=\{\alpha ,\alpha '\}$
. Here,
 ${\mathsf {supp}}(\beta )$
is a basis for the root system
${\mathsf {supp}}(\beta )$
is a basis for the root system
 ${\mathsf {\mathbf {{A}}}}_{p}$
(
${\mathsf {\mathbf {{A}}}}_{p}$
(
 $p\geqslant 2$
) and
$p\geqslant 2$
) and  . Then either
. Then either  and
and  , or
, or  and
and  .
.
Theorem 7.2 Let ![]() be an arbitrary nilradical. Then
be an arbitrary nilradical. Then
Proof
(1) Let
![]() ${\boldsymbol {\zeta }}\in {\mathfrak k}_0$
be a cascade point. Then
${\boldsymbol {\zeta }}\in {\mathfrak k}_0$
be a cascade point. Then ![]() . If
. If
![]() ${\mathfrak n}$
is square integrable, then
${\mathfrak n}$
is square integrable, then ![]() . Hence,
. Hence, ![]() . By Lemma 7.1, this is only possible, if
. By Lemma 7.1, this is only possible, if ![]() . Thus, the implication “
. Thus, the implication “
![]() $\Rightarrow $
” is proved.
$\Rightarrow $
” is proved.
(2) If ![]() , then the assumption on
, then the assumption on ![]() is vacuous and
is vacuous and
![]() ${\mathfrak n}$
is abelian, hence square integrable. Therefore, to prove the implication “
${\mathfrak n}$
is abelian, hence square integrable. Therefore, to prove the implication “
![]() $\Leftarrow $
,” we may assume that
$\Leftarrow $
,” we may assume that ![]() . Then
. Then
![]() ${\mathfrak z}({\mathfrak n})={\mathfrak n}(2)=[{\mathfrak n},{\mathfrak n}]$
and
${\mathfrak z}({\mathfrak n})={\mathfrak n}(2)=[{\mathfrak n},{\mathfrak n}]$
and ![]() . Now, there are two possibilities for
. Now, there are two possibilities for ![]() .
.
• Suppose that ![]() and
and
![]() $[\theta :\alpha ]=2$
.
$[\theta :\alpha ]=2$
.
Set
![]() $\beta _i=\Phi ^{-1}(\alpha )$
. Since
$\beta _i=\Phi ^{-1}(\alpha )$
. Since ![]() , we have
, we have
![]() $[\beta _i:\alpha ]=2$
. Let us prove that
$[\beta _i:\alpha ]=2$
. Let us prove that
![]() $\beta _i$
is the unique minimal element of
$\beta _i$
is the unique minimal element of ![]() . Assume that
. Assume that ![]() , i.e., there is
, i.e., there is ![]() such that
such that
![]() $\beta '\prec \beta $
. Then
$\beta '\prec \beta $
. Then
![]() ${\mathsf {supp}}(\beta ')\subset {\mathsf {supp}}(\beta _i)\setminus \{\alpha \}$
and
${\mathsf {supp}}(\beta ')\subset {\mathsf {supp}}(\beta _i)\setminus \{\alpha \}$
and ![]() . A contradiction! Hence,
. A contradiction! Hence,
![]() $\beta _i$
is minimal in
$\beta _i$
is minimal in ![]() . Assume that there is another minimal element of
. Assume that there is another minimal element of ![]() , say
, say
![]() $\tilde \beta $
. Then
$\tilde \beta $
. Then
![]() ${\mathsf {supp}}(\beta _i)$
and
${\mathsf {supp}}(\beta _i)$
and
![]() ${\mathsf {supp}}(\tilde \beta )$
are disjoint, and we must have
${\mathsf {supp}}(\tilde \beta )$
are disjoint, and we must have ![]() , which is impossible. This contradiction shows that
, which is impossible. This contradiction shows that ![]() .
.
Since
![]() $B{\cdot }{\boldsymbol {\zeta }}$
is dense in
$B{\cdot }{\boldsymbol {\zeta }}$
is dense in
![]() ${\mathfrak n}^{*}$
,
${\mathfrak n}^{*}$
,
![]() $B{\cdot }{\boldsymbol {\zeta }}\subset {\mathfrak n}^{*}_{\mathsf {reg}}$
, and
$B{\cdot }{\boldsymbol {\zeta }}\subset {\mathfrak n}^{*}_{\mathsf {reg}}$
, and
![]() ${\mathfrak n}(2)$
is B-stable, it suffices to prove that
${\mathfrak n}(2)$
is B-stable, it suffices to prove that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}(2)$
(and then, actually,
${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}(2)$
(and then, actually,
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}(2)$
). Recall that
${\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak n}(2)$
). Recall that ![]() . For the unique minimal element
. For the unique minimal element ![]() , we have
, we have
![]() ${\mathfrak h}_i\subset {\mathfrak n}$
and hence
${\mathfrak h}_i\subset {\mathfrak n}$
and hence
![]() ${\mathfrak h}_i\cap {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak g}_{\beta _i}$
. If
${\mathfrak h}_i\cap {\mathfrak n}^{\boldsymbol {\zeta }}={\mathfrak g}_{\beta _i}$
. If
![]() $\beta _i\prec \beta _j$
, then
$\beta _i\prec \beta _j$
, then
![]() $[\beta _j:\alpha ]=2$
and the contribution from
$[\beta _j:\alpha ]=2$
and the contribution from
![]() ${\mathfrak h}_j\cap {\mathfrak n}$
to
${\mathfrak h}_j\cap {\mathfrak n}$
to
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}$
is
${\mathfrak n}^{\boldsymbol {\zeta }}$
is
(see Theorem 4.4). Since ![]() , we have
, we have
![]() ${\mathfrak g}_{\beta _j}\subset {\mathfrak n}(2)$
. The very definition of
${\mathfrak g}_{\beta _j}\subset {\mathfrak n}(2)$
. The very definition of ![]() says that
says that ![]() . Hence,
. Hence,
![]() $[\gamma :\alpha ]=0$
and
$[\gamma :\alpha ]=0$
and
![]() $[\beta _j-\gamma :\alpha ]=2$
. Thus,
$[\beta _j-\gamma :\alpha ]=2$
. Thus, ![]() and
and
![]() ${\mathfrak h}_j\cap {\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}(2)$
.
${\mathfrak h}_j\cap {\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}(2)$
.
• Suppose that ![]() and
and
![]() $[\theta :\alpha ]=[\theta :\alpha ']=1$
.
$[\theta :\alpha ]=[\theta :\alpha ']=1$
.
The argument here is similar to that in the previous part. Set
![]() $\beta =\Phi ^{-1}(\alpha )$
and
$\beta =\Phi ^{-1}(\alpha )$
and
![]() ${\beta '=\Phi ^{-1}(\alpha ')}$
. Using the hypothesis that
${\beta '=\Phi ^{-1}(\alpha ')}$
. Using the hypothesis that ![]() , one first proves that
, one first proves that
![]() $\beta =\beta '$
(hence
$\beta =\beta '$
(hence
![]() $\Phi (\beta )=\{\alpha ,\alpha '\}$
) and that
$\Phi (\beta )=\{\alpha ,\alpha '\}$
) and that
![]() $\beta $
is the unique minimal element of
$\beta $
is the unique minimal element of ![]() . Then the use of Theorem 4.4 allows us to check that
. Then the use of Theorem 4.4 allows us to check that
![]() ${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}(2)$
.
${\mathfrak n}^{\boldsymbol {\zeta }}\subset {\mathfrak n}(2)$
.
Using Theorem 7.2, it is not hard to get the list of square integrable nilradicals in all simple Lie algebras. For ![]() ,
, ![]() is abelian and these cases are well known. If
is abelian and these cases are well known. If ![]() , then
, then ![]() . The condition that
. The condition that ![]() belongs to the highest graded component of
belongs to the highest graded component of ![]() is quite strong. Therefore, not all nilradicals with
is quite strong. Therefore, not all nilradicals with ![]() are square integrable.
are square integrable.
Example 7.3 (1) The list of square integrable nilradicals with ![]() is given below.
is given below.

(2) The list contains all the cases in which
![]() ${\mathfrak n}={\mathfrak h}_1$
is the Heisenberg nilradicals. For the exceptional algebras, this corresponds to
${\mathfrak n}={\mathfrak h}_1$
is the Heisenberg nilradicals. For the exceptional algebras, this corresponds to ![]() indicated first, whereas for the classical series, this corresponds to the cases with
indicated first, whereas for the classical series, this corresponds to the cases with
![]() $k=1$
.
$k=1$
.
(3) Using [Reference Panyushev22], one verifies that ![]() has no CP for
has no CP for
![]() ${\mathsf {\mathbf {{B}}}}_{n}$
with
${\mathsf {\mathbf {{B}}}}_{n}$
with
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
![]() $({\mathsf {\mathbf {{E}}}}_{8}, \alpha _7)$
, and
$({\mathsf {\mathbf {{E}}}}_{8}, \alpha _7)$
, and
![]() $({\mathsf {\mathbf {{F}}}}_{4}, \alpha _1)$
.
$({\mathsf {\mathbf {{F}}}}_{4}, \alpha _1)$
.
(4) For
![]() ${\mathsf {\mathbf {{D}}}}_{2n}$
and
${\mathsf {\mathbf {{D}}}}_{2n}$
and ![]() ,
, ![]() is not square integrable. Indeed, here,
is not square integrable. Indeed, here, ![]() ,
, ![]() , and
, and ![]() contains two elements,
contains two elements,
![]() $\alpha _{2n}=\beta _{2n-1}$
and
$\alpha _{2n}=\beta _{2n-1}$
and
![]() $\alpha _{2n-1}=\beta _{2n}$
. (We use the notation of Appendix A.) Hence,
$\alpha _{2n-1}=\beta _{2n}$
. (We use the notation of Appendix A.) Hence, ![]() , while the other elements of
, while the other elements of ![]() belong to
belong to ![]() . Here,
. Here, ![]() and
and ![]() . (Of course, there are other nilradicals with
. (Of course, there are other nilradicals with ![]() that are not square integrable.)
that are not square integrable.)
Remark 7.4 A real nilpotent Lie group Q has a unitary square integrable representation if and only if
![]() ${\mathrm {ind}}\,{\mathfrak q}=\dim {\mathfrak z}({\mathfrak q})$
[Reference Moore and Wolf15, Theorem 1]. For this reason, Elashvili applied the term “square integrable” to the nilpotent Lie algebras
${\mathrm {ind}}\,{\mathfrak q}=\dim {\mathfrak z}({\mathfrak q})$
[Reference Moore and Wolf15, Theorem 1]. For this reason, Elashvili applied the term “square integrable” to the nilpotent Lie algebras
![]() ${\mathfrak q}$
satisfying that equality, over an algebraically closed field of characteristic zero [Reference Elashvili9] (cf. also [Reference Elashvili and Ooms10]). Afterward, the theory of square integrable representations was extended to the setting of arbitrary Lie groups [Reference Duflo6]. The relevant notions are those of a quasi-reductive Lie group and a coadjoint orbit of reductive type (see [Reference Duflo, Khalgui and Torasso7]). Therefore, Theorem 7.2 provides a classification of the quasi-reductive nilradicals in
${\mathfrak q}$
satisfying that equality, over an algebraically closed field of characteristic zero [Reference Elashvili9] (cf. also [Reference Elashvili and Ooms10]). Afterward, the theory of square integrable representations was extended to the setting of arbitrary Lie groups [Reference Duflo6]. The relevant notions are those of a quasi-reductive Lie group and a coadjoint orbit of reductive type (see [Reference Duflo, Khalgui and Torasso7]). Therefore, Theorem 7.2 provides a classification of the quasi-reductive nilradicals in
![]() ${\mathfrak g}$
. Various results on quasi-reductive seaweed (= biparabolic) subalgebras of
${\mathfrak g}$
. Various results on quasi-reductive seaweed (= biparabolic) subalgebras of
![]() ${\mathfrak g}$
are obtained in [Reference Baur and Moreau1, Reference Moreau and Yakimova16].
${\mathfrak g}$
are obtained in [Reference Baur and Moreau1, Reference Moreau and Yakimova16].
8 When is the quotient morphism equidimensional?
It is well known that if a graded polynomial algebra
![]() ${\mathcal A}$
is a free module over a graded subalgebra
${\mathcal A}$
is a free module over a graded subalgebra
![]() ${\mathcal B}$
, then
${\mathcal B}$
, then
![]() ${\mathcal B}$
is necessarily polynomial. Furthermore, if
${\mathcal B}$
is necessarily polynomial. Furthermore, if
![]() ${\mathcal B}$
is a graded polynomial subalgebra of
${\mathcal B}$
is a graded polynomial subalgebra of
![]() ${\mathcal A}$
, then
${\mathcal A}$
, then
![]() ${\mathcal A}$
is a free
${\mathcal A}$
is a free
![]() ${\mathcal B}$
-module if and only if the induced morphism
${\mathcal B}$
-module if and only if the induced morphism
![]() $\pi : {\mathsf {Spec\,}}({\mathcal A})\to {\mathsf {Spec\,}}({\mathcal B})$
is equidimensional, i.e.,
$\pi : {\mathsf {Spec\,}}({\mathcal A})\to {\mathsf {Spec\,}}({\mathcal B})$
is equidimensional, i.e.,
![]() $\dim \pi ^{-1}(\pi (x))=\dim {\mathcal A}-\dim {\mathcal B}$
for any
$\dim \pi ^{-1}(\pi (x))=\dim {\mathcal A}-\dim {\mathcal B}$
for any
![]() $x\in {\mathsf {Spec\,}}({\mathcal A})$
[Reference Schwarz26, Proposition 17.29]. By a theorem of Chevalley, dominant equidimensional morphisms are open. Therefore, in the graded situation,
$x\in {\mathsf {Spec\,}}({\mathcal A})$
[Reference Schwarz26, Proposition 17.29]. By a theorem of Chevalley, dominant equidimensional morphisms are open. Therefore, in the graded situation,
![]() $\pi $
is also onto (see [Reference Vinberg and Gindikin29, 2.4]).
$\pi $
is also onto (see [Reference Vinberg and Gindikin29, 2.4]).
In this section, we point out certain nilradicals
![]() ${\mathfrak n}$
in
${\mathfrak n}$
in
![]() ${\mathfrak g}$
such that
${\mathfrak g}$
such that ![]() is a free module over
is a free module over ![]() . The last algebra is always polynomial (Lemma 6.1); hence, our task is to guarantee that the quotient morphism
. The last algebra is always polynomial (Lemma 6.1); hence, our task is to guarantee that the quotient morphism
is equidimensional. Since ![]() (Lemma 6.3), the optimal nilradicals of such type provide examples, where
(Lemma 6.3), the optimal nilradicals of such type provide examples, where ![]() is a free module over its Poisson center
is a free module over its Poisson center ![]() . We begin with a simple observation.
. We begin with a simple observation.
Lemma 8.1 If ![]() , then
, then ![]() is a free
is a free ![]() -module.
-module.
Proof By Theorem 6.4, we have ![]() . Since
. Since ![]() is an element of degree
is an element of degree
![]() $1$
, the hyperplane
$1$
, the hyperplane
![]() ${\mathfrak n}^{*}_0=\{\xi \in {\mathfrak n}^{*}\mid \xi (e_{\theta })=0\}$
is U-stable and
${\mathfrak n}^{*}_0=\{\xi \in {\mathfrak n}^{*}\mid \xi (e_{\theta })=0\}$
is U-stable and
![]() ${\mathfrak n}^{*}_0/\!\!/ U\simeq \mathbb A^s$
, where
${\mathfrak n}^{*}_0/\!\!/ U\simeq \mathbb A^s$
, where ![]() . By a result of Brion [Reference Brion3] on invariants of unipotent groups,
. By a result of Brion [Reference Brion3] on invariants of unipotent groups,
![]() $\pi _0:{\mathfrak n}^{*}_0\to {\mathfrak n}^{*}_0/\!\!/ U$
is equidimensional, and this implies that
$\pi _0:{\mathfrak n}^{*}_0\to {\mathfrak n}^{*}_0/\!\!/ U$
is equidimensional, and this implies that
![]() $\pi $
is equidimensional, too.
$\pi $
is equidimensional, too.
Theorem 8.2 Let
![]() ${\mathfrak n}_{\{\alpha \}}$
be an abelian nilradical, i.e.,
${\mathfrak n}_{\{\alpha \}}$
be an abelian nilradical, i.e.,
![]() $[\theta :\alpha ]=1$
. Suppose that a nilradical
$[\theta :\alpha ]=1$
. Suppose that a nilradical
![]() ${\mathfrak n}$
is contained between
${\mathfrak n}$
is contained between
![]() ${\mathfrak n}_{\{\alpha \}}$
and its optimization
${\mathfrak n}_{\{\alpha \}}$
and its optimization
![]() $\widetilde {{\mathfrak n}_{\{\alpha \}}}$
. Then:
$\widetilde {{\mathfrak n}_{\{\alpha \}}}$
. Then:
-
(1)
 ${\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
${\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
 ${\mathfrak n}$
;
${\mathfrak n}$
; -
(2)
 is a free module over
is a free module over  .
.
Proof (1) By Remark 2.4, we have
![]() $\dim {\mathfrak n}_{\{\alpha \}}=\boldsymbol {b}({\mathfrak n}_{\{\alpha \}})=\boldsymbol {b}({\mathfrak n})$
.
$\dim {\mathfrak n}_{\{\alpha \}}=\boldsymbol {b}({\mathfrak n}_{\{\alpha \}})=\boldsymbol {b}({\mathfrak n})$
.
(2) Consider the commutative diagram  corresponding to the U-equivariant inclusion
corresponding to the U-equivariant inclusion
![]() ${\mathfrak n}_{\{\alpha \}}\hookrightarrow {\mathfrak n}$
. Since
${\mathfrak n}_{\{\alpha \}}\hookrightarrow {\mathfrak n}$
. Since
![]() ${\mathfrak n}$
and
${\mathfrak n}$
and
![]() ${\mathfrak n}_{\{\alpha \}}$
have the same optimization, Theorem 6.4 implies that
${\mathfrak n}_{\{\alpha \}}$
have the same optimization, Theorem 6.4 implies that ![]() , i.e.,
, i.e.,
![]() $\varphi /\!\!/ U$
is an isomorphism. By a general result on U-invariants for the abelian nilradicals [Reference Panyushev20, Theorem 4.6],
$\varphi /\!\!/ U$
is an isomorphism. By a general result on U-invariants for the abelian nilradicals [Reference Panyushev20, Theorem 4.6], ![]() is a free module over
is a free module over ![]() . Hence, the morphism
. Hence, the morphism
![]() $\pi _{\{\alpha \}}$
is equidimensional and onto. Because the projection
$\pi _{\{\alpha \}}$
is equidimensional and onto. Because the projection
![]() $\varphi $
is also onto and equidimensional,
$\varphi $
is also onto and equidimensional,
![]() $\pi $
must be equidimensional, too. Since
$\pi $
must be equidimensional, too. Since
![]() ${\mathfrak n}^{*}/\!\!/ U$
is an affine space, the morphism
${\mathfrak n}^{*}/\!\!/ U$
is an affine space, the morphism
![]() $\pi $
is flat and
$\pi $
is flat and
![]() ${\mathbb C}[{\mathfrak n}^{*}]$
is a free
${\mathbb C}[{\mathfrak n}^{*}]$
is a free
![]() ${\mathbb C}[{\mathfrak n}^{*}]^U$
-module.
${\mathbb C}[{\mathfrak n}^{*}]^U$
-module.
Corollary 8.3 For the optimal nilradical
![]() $\tilde {\mathfrak n}=\widetilde {\mathfrak n}_{\{\alpha \}}$
, the algebra
$\tilde {\mathfrak n}=\widetilde {\mathfrak n}_{\{\alpha \}}$
, the algebra ![]() is a free module over
is a free module over ![]() .
.
Theorem 8.2 implies interesting consequences for some types of simple Lie algebras.
Proposition 8.4 For every nilradical
![]() ${\mathfrak n}$
in
${\mathfrak n}$
in
![]() ${\mathfrak {sl}}_{n+1}$
, there is an
${\mathfrak {sl}}_{n+1}$
, there is an
![]() $\alpha \in \Pi $
such that
$\alpha \in \Pi $
such that
![]() ${\mathfrak n}_{\{\alpha \}}\subset {\mathfrak n}\subset \widetilde {{\mathfrak n}_{\{\alpha \}}}$
. Therefore,
${\mathfrak n}_{\{\alpha \}}\subset {\mathfrak n}\subset \widetilde {{\mathfrak n}_{\{\alpha \}}}$
. Therefore, ![]() is a free module over
is a free module over ![]() for any
for any
![]() ${\mathfrak n}$
.
${\mathfrak n}$
.
Proof We use the notation of Example 2.5(1). Recall that
![]() $[\theta :\alpha ]=1$
for each
$[\theta :\alpha ]=1$
for each
![]() $\alpha \in \Pi $
. If
$\alpha \in \Pi $
. If ![]() and
and ![]() (
(
![]() $k\leqslant [(n+1)]/2$
), then
$k\leqslant [(n+1)]/2$
), then ![]() . Then any
. Then any
![]() $\alpha $
in this intersection will do. (The construction of such a simple root
$\alpha $
in this intersection will do. (The construction of such a simple root
![]() $\alpha $
is essentially contained in the proof of Theorem 6.2 in [Reference Elashvili and Ooms10]. For, then
$\alpha $
is essentially contained in the proof of Theorem 6.2 in [Reference Elashvili and Ooms10]. For, then
![]() ${\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
${\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
![]() ${\mathfrak n}$
. But our approach that refers to
${\mathfrak n}$
. But our approach that refers to ![]() is shorter.)
is shorter.)
Of course, the first assertion of Proposition 8.4 appears to be true because all simple roots of
![]() ${\mathfrak {sl}}_{n+1}$
provide abelian nilradicals. Nevertheless, the second assertion can be proved for the nilradicals in
${\mathfrak {sl}}_{n+1}$
provide abelian nilradicals. Nevertheless, the second assertion can be proved for the nilradicals in
![]() ${\mathfrak {sp}}_{2n}$
, although the proof becomes more involved.
${\mathfrak {sp}}_{2n}$
, although the proof becomes more involved.
Proposition 8.5 For any nilradical
![]() ${\mathfrak n}$
in
${\mathfrak n}$
in
![]() ${\mathfrak {sp}}_{2n}$
,
${\mathfrak {sp}}_{2n}$
, ![]() is a free module over
is a free module over ![]() .
.
Proof Here,
![]() ${\mathfrak n}_{\{\alpha _{n}\}}$
is the only abelian nilradical and
${\mathfrak n}_{\{\alpha _{n}\}}$
is the only abelian nilradical and ![]() . Hence,
. Hence,
![]() $\widetilde {{\mathfrak n}_{\{\alpha _{n}\}}}={\mathfrak u}$
.
$\widetilde {{\mathfrak n}_{\{\alpha _{n}\}}}={\mathfrak u}$
.
(1) If ![]() and
and ![]() , then
, then
![]() ${\mathfrak n}_{\{\alpha _{n}\}}\subset {\mathfrak n}$
and Theorem 8.2 applies. In particular, this shows that here
${\mathfrak n}_{\{\alpha _{n}\}}\subset {\mathfrak n}$
and Theorem 8.2 applies. In particular, this shows that here ![]() is a free module over
is a free module over ![]() .
.
(2) Suppose that ![]() . Then
. Then ![]() for some
for some
![]() $k<n$
,
$k<n$
, ![]() , and
, and
![]() ${\mathfrak a}:={\mathfrak n}\cap {\mathfrak n}_{\{\alpha _{n}\}}$
is a CP-ideal of
${\mathfrak a}:={\mathfrak n}\cap {\mathfrak n}_{\{\alpha _{n}\}}$
is a CP-ideal of
![]() ${\mathfrak n}$
. If
${\mathfrak n}$
. If
![]() ${\mathfrak n}_{\{\alpha _{n}\}}$
is identified with the space
${\mathfrak n}_{\{\alpha _{n}\}}$
is identified with the space
![]() $\widehat {\mathsf {Sym}}_n$
of
$\widehat {\mathsf {Sym}}_n$
of
![]() $n\times n$
matrices that are symmetric w.r.t. the antidiagonal (see Example 2.6), then
$n\times n$
matrices that are symmetric w.r.t. the antidiagonal (see Example 2.6), then

Since
![]() ${\mathfrak a}$
is a
${\mathfrak a}$
is a
![]() ${\mathfrak b}$
-stable ideal of
${\mathfrak b}$
-stable ideal of
![]() ${\mathfrak u}$
,
${\mathfrak u}$
, ![]() is a polynomial algebra (see Remark 6.5). Let us prove that
is a polynomial algebra (see Remark 6.5). Let us prove that ![]() is a free
is a free ![]() -module, i.e., that
-module, i.e., that
![]() $\bar \pi :{\mathfrak a}^{*}\to {\mathfrak a}^{*}/\!\!/ U$
is equidimensional. Consider the commutative diagram
$\bar \pi :{\mathfrak a}^{*}\to {\mathfrak a}^{*}/\!\!/ U$
is equidimensional. Consider the commutative diagram

corresponding to the U-equivariant inclusion
![]() ${\mathfrak a}\hookrightarrow {\mathfrak n}_{\{\alpha _{n}\}}$
. Here,
${\mathfrak a}\hookrightarrow {\mathfrak n}_{\{\alpha _{n}\}}$
. Here, ![]() (cf. Section 3.4(2)), i.e.,
(cf. Section 3.4(2)), i.e., ![]() . Upon the identification of
. Upon the identification of
![]() ${\mathfrak n}_{\{\alpha _{n}\}}^{*}$
with
${\mathfrak n}_{\{\alpha _{n}\}}^{*}$
with
 ${\mathfrak n}_{\{\alpha _{n}\}}^-=\left \{\begin {pmatrix} 0 & 0 \\ C & 0\end {pmatrix}\mid C=\hat C \right \}$
and thereby with the dual space
${\mathfrak n}_{\{\alpha _{n}\}}^-=\left \{\begin {pmatrix} 0 & 0 \\ C & 0\end {pmatrix}\mid C=\hat C \right \}$
and thereby with the dual space
![]() $\widehat {\mathsf {Sym}}^{*}_n$
, the algebra
$\widehat {\mathsf {Sym}}^{*}_n$
, the algebra
![]() ${\mathbb C}[{\mathfrak n}_{\{\alpha _{n}\}}^{*}]^U$
is freely generated by the principal minors of C. Let
${\mathbb C}[{\mathfrak n}_{\{\alpha _{n}\}}^{*}]^U$
is freely generated by the principal minors of C. Let
![]() $f_i$
be the principal minor of degree i; see the figure
$f_i$
be the principal minor of degree i; see the figure  . Then
. Then ![]() and
and
![]() $\pi _{\alpha _n}(M)=(f_1(M),\dots ,f_n(M))$
. On the other hand,
$\pi _{\alpha _n}(M)=(f_1(M),\dots ,f_n(M))$
. On the other hand, ![]() for
for
![]() $i\leqslant k$
and hence
$i\leqslant k$
and hence ![]() . Furthermore, if
. Furthermore, if
![]() $\bar M=\psi (M)\in {\mathfrak a}^{*}$
, then
$\bar M=\psi (M)\in {\mathfrak a}^{*}$
, then
![]() $f_i(\bar M)=f_i(M)$
for
$f_i(\bar M)=f_i(M)$
for
![]() $i\leqslant k$
. Then
$i\leqslant k$
. Then
![]() $\psi /\!\!/ U$
takes
$\psi /\!\!/ U$
takes
![]() $(f_1(M),\dots ,f_n(M))$
to
$(f_1(M),\dots ,f_n(M))$
to
![]() $(f_1(M),\dots ,f_k(M))$
and thereby
$(f_1(M),\dots ,f_k(M))$
and thereby
![]() $\psi /\!\!/ U$
is surjective and equidimensional. Since we have already proved that
$\psi /\!\!/ U$
is surjective and equidimensional. Since we have already proved that
![]() $\pi _{\alpha _n}$
is onto and equidimensional, this yields the same conclusion for
$\pi _{\alpha _n}$
is onto and equidimensional, this yields the same conclusion for
![]() $\bar \pi $
.
$\bar \pi $
.
Once it is proved that
![]() $\bar \pi $
is onto and equidimensional, an argument similar to that in Theorem 8.2 can be applied to the embedding
$\bar \pi $
is onto and equidimensional, an argument similar to that in Theorem 8.2 can be applied to the embedding
![]() ${\mathfrak a}\hookrightarrow {\mathfrak n}$
. Consider the diagram
${\mathfrak a}\hookrightarrow {\mathfrak n}$
. Consider the diagram
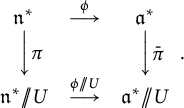
Since
![]() ${\mathfrak a}$
is a CP-ideal of
${\mathfrak a}$
is a CP-ideal of
![]() ${\mathfrak n}$
, we have
${\mathfrak n}$
, we have ![]() [Reference Panyushev22, Proposition 5.5]. Hence,
[Reference Panyushev22, Proposition 5.5]. Hence, ![]() and thereby
and thereby ![]() , i.e.,
, i.e.,
![]() $\phi /\!\!/ U$
is an isomorphism. This implies that
$\phi /\!\!/ U$
is an isomorphism. This implies that
![]() $\pi $
is equidimensional, and we are done.
$\pi $
is equidimensional, and we are done.
The proofs of Propositions 8.4 and 8.5 exploit the fact that every nilradical in
![]() ${\mathfrak {sl}}_{n+1}$
or
${\mathfrak {sl}}_{n+1}$
or
![]() ${\mathfrak {sp}}_{2n}$
has a CP (and hence a CP-ideal). Using Theorem 6.4, we get a joint corollary to these propositions:
${\mathfrak {sp}}_{2n}$
has a CP (and hence a CP-ideal). Using Theorem 6.4, we get a joint corollary to these propositions:
For
![]() ${\mathfrak n}\ne \tilde {\mathfrak n}$
, one cannot even guarantee that
${\mathfrak n}\ne \tilde {\mathfrak n}$
, one cannot even guarantee that ![]() is a polynomial algebra (see Example 6.10). It might be interesting to characterize non-optimal nilradicals having a polynomial algebra
is a polynomial algebra (see Example 6.10). It might be interesting to characterize non-optimal nilradicals having a polynomial algebra ![]() .
.
By [Reference Panyushev22], if
![]() ${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha \}}$
with
${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha \}}$
with
![]() $[\theta :\alpha ]=1$
, then
$[\theta :\alpha ]=1$
, then
![]() ${\mathfrak n}$
has a CP. However, to point out a CP-ideal of
${\mathfrak n}$
has a CP. However, to point out a CP-ideal of
![]() ${\mathfrak n}$
, one needs some precautions:
${\mathfrak n}$
, one needs some precautions:
(1) If
![]() $\Phi (\Phi ^{-1}(\alpha ))=\{\alpha \}$
, then
$\Phi (\Phi ^{-1}(\alpha ))=\{\alpha \}$
, then
![]() ${\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
${\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
![]() ${\mathfrak n}$
.
${\mathfrak n}$
.
(2) If
![]() $\Phi (\Phi ^{-1}(\alpha ))=\{\alpha ,\alpha '\}$
and
$\Phi (\Phi ^{-1}(\alpha ))=\{\alpha ,\alpha '\}$
and
![]() ${\mathfrak g}\ne {\mathfrak {sl}}_{n+1}$
, then at least one of
${\mathfrak g}\ne {\mathfrak {sl}}_{n+1}$
, then at least one of
![]() ${\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
and
${\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
and
![]() ${\mathfrak n}\cap {\mathfrak n}_{\alpha '}$
is a CP-ideal of
${\mathfrak n}\cap {\mathfrak n}_{\alpha '}$
is a CP-ideal of
![]() ${\mathfrak n}$
.
${\mathfrak n}$
.
(3) If
![]() ${\mathfrak g}={\mathfrak {sl}}_{n+1}$
, then one should choose the minimal
${\mathfrak g}={\mathfrak {sl}}_{n+1}$
, then one should choose the minimal
![]() $\widetilde {\mathfrak n}_{\{\alpha \}}$
containing
$\widetilde {\mathfrak n}_{\{\alpha \}}$
containing
![]() ${\mathfrak n}$
. More precisely, since
${\mathfrak n}$
. More precisely, since
![]() ${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha \}}$
, we have
${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha \}}$
, we have ![]() . Here, one has to take
. Here, one has to take
![]() $\alpha $
such that
$\alpha $
such that ![]() . Then item (2) applies.
. Then item (2) applies.
In any case,
![]() ${\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
${\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
![]() ${\mathfrak n}$
for a “right” choice of
${\mathfrak n}$
for a “right” choice of
![]() $\alpha \in \Pi $
, and the hypothesis that
$\alpha \in \Pi $
, and the hypothesis that
![]() ${\mathfrak n}_{\{\alpha \}}\subset {\mathfrak n}$
is not required for the presence of CP. That is, Theorem 8.2 does not apply to all nilradicals with CP. Nevertheless, using a case-by-case argument, we can prove the following.
${\mathfrak n}_{\{\alpha \}}\subset {\mathfrak n}$
is not required for the presence of CP. That is, Theorem 8.2 does not apply to all nilradicals with CP. Nevertheless, using a case-by-case argument, we can prove the following.
Theorem 8.6 If ![]() has a CP, then
has a CP, then ![]() is a free
is a free ![]() -module.
-module.
Proof By the preceding discussion, we may assume that
![]() ${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha \}}$
and
${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha \}}$
and
![]() ${\mathfrak a}:={\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
${\mathfrak a}:={\mathfrak n}\cap {\mathfrak n}_{\{\alpha \}}$
is a CP-ideal of
![]() ${\mathfrak n}$
. As in the proof of Proposition 8.5, one has the commutative diagram (8.1), where
${\mathfrak n}$
. As in the proof of Proposition 8.5, one has the commutative diagram (8.1), where
![]() $\phi /\!\!/ U$
is an isomorphism. Therefore, it suffices to prove that
$\phi /\!\!/ U$
is an isomorphism. Therefore, it suffices to prove that
![]() $\bar {\pi }:{\mathfrak a}^{*}\to {\mathfrak a}^{*}/\!\!/ U$
is equidimensional. Consider all simple Lie algebras having abelian nilradicals.
$\bar {\pi }:{\mathfrak a}^{*}\to {\mathfrak a}^{*}/\!\!/ U$
is equidimensional. Consider all simple Lie algebras having abelian nilradicals.
(1) The algebras
![]() ${\mathfrak {sl}}_{n+1}$
and
${\mathfrak {sl}}_{n+1}$
and
![]() ${\mathfrak {sp}}_{2n}$
have been considered above.
${\mathfrak {sp}}_{2n}$
have been considered above.
(2) For
![]() ${\mathfrak {so}}_{2n+1}$
, the only abelian nilradical corresponds to
${\mathfrak {so}}_{2n+1}$
, the only abelian nilradical corresponds to
![]() $\alpha _1=\varepsilon _1-\varepsilon _2$
and
$\alpha _1=\varepsilon _1-\varepsilon _2$
and ![]() . Therefore,
. Therefore, ![]() and Lemma 8.1 applies.
and Lemma 8.1 applies.
(3) For
![]() ${\mathfrak {so}}_{2n}$
, the abelian nilradicals correspond to
${\mathfrak {so}}_{2n}$
, the abelian nilradicals correspond to
![]() $\alpha _1,\alpha _{n-1}$
, and
$\alpha _1,\alpha _{n-1}$
, and
![]() $\alpha _n=\varepsilon _{n-1}+\varepsilon _n$
.
$\alpha _n=\varepsilon _{n-1}+\varepsilon _n$
.
• For
![]() $\alpha _1=\varepsilon _1-\varepsilon _2$
, the situation is the same as for
$\alpha _1=\varepsilon _1-\varepsilon _2$
, the situation is the same as for
![]() ${\mathfrak g}={\mathfrak {so}}_{2n+1}$
.
${\mathfrak g}={\mathfrak {so}}_{2n+1}$
.
• Since
![]() ${\mathfrak n}_{\{\alpha _{n-1}\}}\simeq {\mathfrak n}_{\{\alpha _{n}\}}$
, we consider only the last possibility. The case of
${\mathfrak n}_{\{\alpha _{n-1}\}}\simeq {\mathfrak n}_{\{\alpha _{n}\}}$
, we consider only the last possibility. The case of
![]() $({\mathfrak {so}}_{2n}, \alpha _n)$
is similar to
$({\mathfrak {so}}_{2n}, \alpha _n)$
is similar to
![]() $({\mathfrak {sp}}_{2n}, \alpha _n)$
, which is considered in Proposition 8.5. The distinction is that now
$({\mathfrak {sp}}_{2n}, \alpha _n)$
, which is considered in Proposition 8.5. The distinction is that now
![]() ${\mathfrak n}_{\{\alpha _{n}\}}$
consists of
${\mathfrak n}_{\{\alpha _{n}\}}$
consists of
![]() $n\times n$
matrices that are skew-symmetric w.r.t. the antidiagonal, and the basic U-invariants are pfaffians of the principal minors of even order. The embedding
$n\times n$
matrices that are skew-symmetric w.r.t. the antidiagonal, and the basic U-invariants are pfaffians of the principal minors of even order. The embedding
![]() ${\mathfrak a}\subset {\mathfrak n}_{\{\alpha _{n}\}}$
can be described by the figure in the proof of Proposition 8.5, only now k must be even and the matrices should be skew-symmetric w.r.t. the antidiagonal.
${\mathfrak a}\subset {\mathfrak n}_{\{\alpha _{n}\}}$
can be described by the figure in the proof of Proposition 8.5, only now k must be even and the matrices should be skew-symmetric w.r.t. the antidiagonal.
More precisely, if
![]() $n=2p+1$
, then
$n=2p+1$
, then ![]() and
and
![]() $\Phi ^{-1}(\alpha _n)=\beta _{2p-1}$
. If
$\Phi ^{-1}(\alpha _n)=\beta _{2p-1}$
. If
![]() $n=2p$
, then
$n=2p$
, then
![]() $\alpha _{n}=\beta _{2p-1}$
. In both cases,
$\alpha _{n}=\beta _{2p-1}$
. In both cases, ![]() . If
. If
![]() ${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha _{n}\}}$
and
${\mathfrak n}\subset \widetilde {\mathfrak n}_{\{\alpha _{n}\}}$
and
![]() ${\mathfrak n}_{\{\alpha \}}\not \subset {\mathfrak n}$
, then
${\mathfrak n}_{\{\alpha \}}\not \subset {\mathfrak n}$
, then ![]() , where
, where
![]() $s<p=[n/2]$
. Then
$s<p=[n/2]$
. Then ![]() and
and ![]() is generated by the pfaffians of order
is generated by the pfaffians of order
![]() $2,4,\dots ,2s$
. The fact that these pfaffians form a regular sequence in
$2,4,\dots ,2s$
. The fact that these pfaffians form a regular sequence in ![]() can be proved as in Proposition 8.5 for
can be proved as in Proposition 8.5 for
![]() ${\mathfrak {sp}}_{2n}$
.
${\mathfrak {sp}}_{2n}$
.
(4) For
![]() ${\mathsf {\mathbf {{E}}}}_{6}$
, the abelian nilradicals correspond to
${\mathsf {\mathbf {{E}}}}_{6}$
, the abelian nilradicals correspond to
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _5$
. In both cases, we have
$\alpha _5$
. In both cases, we have ![]() and hence Lemma 8.1 applies to any
and hence Lemma 8.1 applies to any
![]() ${\mathfrak n}\subset \widetilde {{\mathfrak n}_{\{\alpha _i\}}}$
,
${\mathfrak n}\subset \widetilde {{\mathfrak n}_{\{\alpha _i\}}}$
,
![]() $i=1,5$
.
$i=1,5$
.
(5) For
![]() ${\mathsf {\mathbf {{E}}}}_{7}$
, the only abelian nilradical corresponds to
${\mathsf {\mathbf {{E}}}}_{7}$
, the only abelian nilradical corresponds to
![]() $\alpha _1$
. Here,
$\alpha _1$
. Here, ![]() (see Appendix A). Therefore, Lemma 8.1 applies here.
(see Appendix A). Therefore, Lemma 8.1 applies here.
Our computations suggest that Theorem 8.6 holds in the general case.
Conjecture 8.7 For any nilradical
![]() ${\mathfrak n}$
in a simple Lie algebra
${\mathfrak n}$
in a simple Lie algebra
![]() ${\mathfrak g}$
,
${\mathfrak g}$
, ![]() is a free
is a free ![]() -module. In particular, for any optimal nilradical
-module. In particular, for any optimal nilradical
![]() $\tilde {\mathfrak n}$
,
$\tilde {\mathfrak n}$
, ![]() is a free
is a free ![]() -module.
-module.
So far, this conjecture is proved for (i) the square integrable nilradicals (Section 7), (ii) the nilradicals with CP, (iii) the series
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
and
${\mathsf {\mathbf {{A}}}}_{n}$
and
![]() ${\mathsf {\mathbf {{C}}}}_{n}$
, and (iv) if
${\mathsf {\mathbf {{C}}}}_{n}$
, and (iv) if
![]() ${\mathsf {rk\,}}{\mathfrak g}\leqslant 3$
. It is not hard to check it for
${\mathsf {rk\,}}{\mathfrak g}\leqslant 3$
. It is not hard to check it for
![]() ${\mathsf {\mathbf {{D}}}}_{4}$
. Perhaps, the first step toward a general proof is to verify the conjecture for
${\mathsf {\mathbf {{D}}}}_{4}$
. Perhaps, the first step toward a general proof is to verify the conjecture for
![]() ${\mathfrak n}={\mathfrak u}$
. Since
${\mathfrak n}={\mathfrak u}$
. Since
![]() ${\mathfrak u}$
has a CP only for
${\mathfrak u}$
has a CP only for
![]() ${\mathsf {\mathbf {{A}}}}_{n}$
and
${\mathsf {\mathbf {{A}}}}_{n}$
and
![]() ${\mathsf {\mathbf {{C}}}}_{n}$
, some fresh ideas are necessary here.
${\mathsf {\mathbf {{C}}}}_{n}$
, some fresh ideas are necessary here.
A The elements of 
We list below the cascade roots (elements of ![]() ) for all simple Lie algebras. The numbering of
) for all simple Lie algebras. The numbering of
![]() $\Pi =\{\alpha _1,\dots ,\alpha _{{\mathsf {rk\,}} {\mathfrak g}}\}$
follows [Reference Onishchik and Vinberg17, Table 1] and, for roots of the classical Lie algebras, we use the standard
$\Pi =\{\alpha _1,\dots ,\alpha _{{\mathsf {rk\,}} {\mathfrak g}}\}$
follows [Reference Onishchik and Vinberg17, Table 1] and, for roots of the classical Lie algebras, we use the standard
![]() $\varepsilon $
-notation. The numbering of cascade roots yields a linear extension of the poset
$\varepsilon $
-notation. The numbering of cascade roots yields a linear extension of the poset ![]() , i.e., it is not unique unless
, i.e., it is not unique unless ![]() is a chain. In all cases,
is a chain. In all cases,
![]() $\beta _1=\theta $
and
$\beta _1=\theta $
and
In particular, if ![]() , then
, then
![]() $\Phi (\beta )=\{\beta \}$
and
$\Phi (\beta )=\{\beta \}$
and
![]() $\beta $
is a minimal element of
$\beta $
is a minimal element of ![]() . Conversely, if
. Conversely, if
![]() $\beta $
is a minimal element of
$\beta $
is a minimal element of ![]() and
and
![]() $\Phi (\beta )=\{\alpha \}$
, a sole simple root, then
$\Phi (\beta )=\{\alpha \}$
, a sole simple root, then
![]() $\alpha =\beta $
.
$\alpha =\beta $
.
The cascade elements for the classical Lie algebras :
-
 ${\mathsf {\mathbf {{A}}}}_{n}, n\geqslant 2$
${\mathsf {\mathbf {{A}}}}_{n}, n\geqslant 2$
 $\beta _i=\varepsilon _i-\varepsilon _{n+2-i}=\alpha _i+\dots +\alpha _{n+1-i}$
$\beta _i=\varepsilon _i-\varepsilon _{n+2-i}=\alpha _i+\dots +\alpha _{n+1-i}$
 $\Big (i=1,2,\dots ,\left [\frac {n+1}{2}\right ]\Big )$
;
$\Big (i=1,2,\dots ,\left [\frac {n+1}{2}\right ]\Big )$
; -
 ${\mathsf {\mathbf {{C}}}}_{n}, n\geqslant 1$
${\mathsf {\mathbf {{C}}}}_{n}, n\geqslant 1$
 $\beta _i=2\varepsilon _i=2(\alpha _i+\dots +\alpha _{n-1})+\alpha _n$
(
$\beta _i=2\varepsilon _i=2(\alpha _i+\dots +\alpha _{n-1})+\alpha _n$
(
 $i=1,2,\dots ,n-1$
) and
$i=1,2,\dots ,n-1$
) and
 $\beta _n=2\varepsilon _n=\alpha _n$
;
$\beta _n=2\varepsilon _n=\alpha _n$
; -
 ${\mathsf {\mathbf {{B}}}}_{2n}$
,
${\mathsf {\mathbf {{B}}}}_{2n}$
,
 ${\mathsf {\mathbf {{D}}}}_{2n}$
,
${\mathsf {\mathbf {{D}}}}_{2n}$
,
 ${\mathsf {\mathbf {{D}}}}_{2n+1}$
(
${\mathsf {\mathbf {{D}}}}_{2n+1}$
(
 $n\geqslant 2$
)
$n\geqslant 2$
)
 $\beta _{2i-1}=\varepsilon _{2i-1}+\varepsilon _{2i}$
,
$\beta _{2i-1}=\varepsilon _{2i-1}+\varepsilon _{2i}$
,
 $\beta _{2i}=\varepsilon _{2i-1}{-}\varepsilon _{2i}=\alpha _{2i-1}$
(
$\beta _{2i}=\varepsilon _{2i-1}{-}\varepsilon _{2i}=\alpha _{2i-1}$
(
 $i=1,2,\dots ,n$
);
$i=1,2,\dots ,n$
); -
 ${\mathsf {\mathbf {{B}}}}_{2n+1}, n\geqslant 1$
here
${\mathsf {\mathbf {{B}}}}_{2n+1}, n\geqslant 1$
here
 $\beta _1,\dots ,\beta _{2n}$
are as above and
$\beta _1,\dots ,\beta _{2n}$
are as above and
 $\beta _{2n+1}=\varepsilon _{2n+1}=\alpha _{2n+1}$
.
$\beta _{2n+1}=\varepsilon _{2n+1}=\alpha _{2n+1}$
.
For all orthogonal series, we have
![]() $\beta _{2i}=\alpha _{2i-1}$
,
$\beta _{2i}=\alpha _{2i-1}$
,
![]() $i=1,\dots ,n$
, while formulae for
$i=1,\dots ,n$
, while formulae for
![]() $\beta _{2i-1}$
via
$\beta _{2i-1}$
via
![]() $\Pi $
slightly differ for different series. For example, for
$\Pi $
slightly differ for different series. For example, for
![]() ${\mathsf {\mathbf {{D}}}}_{2n}$
one has
${\mathsf {\mathbf {{D}}}}_{2n}$
one has
![]() $\beta _{2i-1}=\alpha _{2i-1}+2(\alpha _{2i}+\dots +\alpha _{2n-2})+\alpha _{2n-1}+\alpha _{2n}$
(
$\beta _{2i-1}=\alpha _{2i-1}+2(\alpha _{2i}+\dots +\alpha _{2n-2})+\alpha _{2n-1}+\alpha _{2n}$
(
![]() $i=1,2,\dots ,n-1$
) and
$i=1,2,\dots ,n-1$
) and
![]() $\beta _{2n-1}=\alpha _{2n}$
.
$\beta _{2n-1}=\alpha _{2n}$
.
The cascade elements for the exceptional Lie algebras :
-
 ${\mathsf {\mathbf {{G}}}}_{2}$
${\mathsf {\mathbf {{G}}}}_{2}$
 $\beta _1=(32)=3\alpha _1+2\alpha _2, \ \beta _2=(10)=\alpha _1$
;
$\beta _1=(32)=3\alpha _1+2\alpha _2, \ \beta _2=(10)=\alpha _1$
; -
 ${\mathsf {\mathbf {{F}}}}_{4}$
${\mathsf {\mathbf {{F}}}}_{4}$
 $\beta _1=(2432)=2\alpha _1{+}4\alpha _2{+}3\alpha _3{+}2\alpha _4,\ \beta _2=(2210),\ \beta _3=(0210),\ \beta _4=(0010)=\alpha _3$
;
$\beta _1=(2432)=2\alpha _1{+}4\alpha _2{+}3\alpha _3{+}2\alpha _4,\ \beta _2=(2210),\ \beta _3=(0210),\ \beta _4=(0010)=\alpha _3$
; -
 ${\mathsf {\mathbf {{E}}}}_{6}$
${\mathsf {\mathbf {{E}}}}_{6}$
 ,
,  ,
,  ,
,  ;
; -
 ${\mathsf {\mathbf {{E}}}}_{7}$
${\mathsf {\mathbf {{E}}}}_{7}$
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ;
; -
 ${\mathsf {\mathbf {{E}}}}_{8}$
${\mathsf {\mathbf {{E}}}}_{8}$
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
For the reader’s convenience, we provide the Hasse diagram of the cascade posets for
![]() ${\mathsf {\mathbf {{D}}}}_{n}$
and
${\mathsf {\mathbf {{D}}}}_{n}$
and
![]() ${\mathsf {\mathbf {{E}}}}_{n}$
. The node “i” in the diagram represents
${\mathsf {\mathbf {{E}}}}_{n}$
. The node “i” in the diagram represents ![]() , and we attach the set
, and we attach the set
![]() $\Phi (\beta _i)\subset \Pi $
to it.
$\Phi (\beta _i)\subset \Pi $
to it.





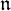
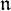
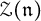 of the symmetric algebra
of the symmetric algebra 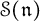 , (iii) the structure of
, (iii) the structure of 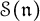 as
as 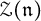 -module, and (iv) the description of square integrable (= quasi-reductive) nilradicals. Our main technical tools are the Kostant cascade in the set of positive roots of
-module, and (iv) the description of square integrable (= quasi-reductive) nilradicals. Our main technical tools are the Kostant cascade in the set of positive roots of