Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T13:12:20.613Z Has data issue: false hasContentIssue false
  • English
  • Français

From Quantum Groups to Groups

Published online by Cambridge University Press:  20 November 2018

Mehrdad Kalantar  and
Matthias Neufang
Mehrdad Kalantar
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, Ontario K1S 5B6, e-mail: mkalanta@math.carleton.ca
Matthias Neufang
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, Ontario, K1S 5B6, e-mail: mneufang@math.carleton.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

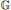In this paper we use the recent developments in the representation theory of locally compact quantum groups, to assign to each locally compact quantum group $\mathbb{G}$ a locally compact group 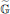$\tilde{\mathbb{G}}$ that is the quantum version of point-masses and is an invariant for the latter. We show that “quantum point-masses” can be identified with several other locally compact groups that can be naturally assigned to the quantum group 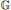$\mathbb{G}$. This assignment preserves compactness as well as discreteness (hence also finiteness), and for large classes of quantum groups, amenability. We calculate this invariant for some of the most well-known examples of non-classical quantum groups. Also, we show that several structural properties of 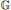$\mathbb{G}$ are encoded by 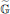$\tilde{\mathbb{G}}$ the latter, despite being a simpler object, can carry very important information about 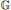$\mathbb{G}$.

Keywords

46L89locally compact quantum grouplocally compact groupvon Neumann algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 5 , 01 October 2013 , pp. 1073 - 1094
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Baaj, S. and Skandalis, G., Unitaires multiplicatifs et dualité pour les produits croisés de C*-algèbres. Ann. Sci. École Norm. Sup. 26(1993), 425–488.Google Scholar
[2] Baaj, S. and Vaes, S., Double crossed products of locally compact quantum groups. J. Inst. Math. Jussieu 4(2005), 135–173. http://dx.doi.org/10.1017/S1474748005000034 Google Scholar
[3] edos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003), 865–884. http://dx.doi.org/10.1142/S0129167X03002046 Google Scholar
[4] Connes, A., Classification of injective factors. Ann. of Math. (2) 104(1976), 73–115. http://dx.doi.org/10.2307/1971057 Google Scholar
[5] de Cannière, J., On the intrinsic group of a Kac algebra. Proc. London Math. Soc. (3) 40(1980), 1–20. http://dx.doi.org/10.1112/plms/s3-40.1.1 Google Scholar
[6] De Commer, K. and Van Daele, A., Algebraic quantum groups imbedded in C*-algebraic quantum groups. Rocky Mountain J. Math. 40(2010), 1149–1182. http://dx.doi.org/10.1216/RMJ-2010-40-4-1149 Google Scholar
[7] Effros, E. G. and Ruan, Z.-J., Operator Spaces. London Math. Soc. Monogr. New Series 23, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[8] Enock, M. and Schwartz, J. M., Kac Algebras and Duality of Locally Compact Groups. Springer-Verlag, Berlin, 1992.Google Scholar
[9] Forrest, B. and Runde, V., Amenability and weak amenability of the Fourier algebra. Math. Z. 250(2005), 731–744. http://dx.doi.org/10.1007/s00209-005-0772-2 Google Scholar
[10] Haagerup, U., The standard form of von Neumann algebras. Math. Scand. 37(1975), 271–283.Google Scholar
[11] Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. Vol. I. Structure of Topological Groups, Integration Theory, Group Representations. Second edition. Grundlehren Math.Wiss. 115, Springer-Verlag, Berlin–New York, 1979.Google Scholar
[12] Hu, Z., Neufang, M., and Ruan, Z.-J., Completely bounded multipliers over locally compact quantum groups. Proc. London Math. Soc., to appear. http://dx.doi.org/10.1112/plms/pdq041 Google Scholar
[13] Johnson, B. E., Cohomology in Banach algebras. Memoirs of the American Mathematical Society, 127, American Mathematical Society, Providence, RI, 1972.Google Scholar
[14] Junge, M., Neufang, M., Ruan, Z.-J., A representation theorem for locally compact quantum groups. Internat. J. Math. 20(2009), 377–400. http://dx.doi.org/10.1142/S0129167X09005285 Google Scholar
[15] Kalantar, M., Towards harmonic analysis on locally compact quantum groups: From Groups to Quantum Groups and Back. Ph.D. thesis, Carleton University, Ottawa, 2010.Google Scholar
[16] Kustermans, J., Locally compact quantum groups in the universal setting. Internat. J. Math. 12(2001), 289–338.Google Scholar
[17] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sci. Ecole Norm. Sup. 33(2000), 837–934.Google Scholar
[18] Kustermans, J., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), 68–92.Google Scholar
[19] Leptin, H., Sur l’algèbre de Fourier d’un groupe localement compact. C. R. Acad. Sci. Paris Sér. A–B 266 (1968), A1180–A1182.Google Scholar
[20] Müller, A., Classifying spaces for quantum principal bundles. Comm. Math. Phys. 149(1992), 495–512. http://dx.doi.org/10.1007/BF02096940 Google Scholar
[21] Renaud, P. F., Centralizers of Fourier algebra of an amenable group. Proc. Amer. Math. Soc. 32(1972), 539–542.Google Scholar
[22] Ruan, Z.-J., The operator amenability of A(G). Amer. J. Math. 117(1995), 1449–1474. http://dx.doi.org/10.2307/2375026 Google Scholar
[23] Runde, V., Lectures on Amenability. Lecture Notes in Math. 1774, Springer-Verlag, Berlin, 2002.Google Scholar
[24] Takesaki, M., A characterization of group algebras as a converse of Tannaka–Stinespring–Tatsuuma duality theorem. Amer. J. Math. 91(1969), 529–564. http://dx.doi.org/10.2307/2373525 Google Scholar
[25] Takesaki, M., Theory of Operator Algebras. II. Encyclopaedia Math. Sci. 125, Operator Algebras and Non-commutative Geometry 6. Springer-Verlag, Berlin, 2003.Google Scholar
[26] Vaes, S., Locally Compact Quantum Groups. Ph.D. thesis, K.U. Leuven, 2000.Google Scholar
[27] G.Wendel, J., Left centralizers and isomorphisms of group algebras. Pacific J. Math. 2(1952), 251–261.Google Scholar
[28] L.Woronowicz, S., Compact matrix pseudogroups. Comm. Math. Phys. 111(1987), 613–665. http://dx.doi.org/10.1007/BF01219077 Google Scholar
[29] L.Woronowicz, S., Compact quantum groups. In: Sym´etries quantiques (Les Houches, 1995), North-Holland, Amsterdam, 1998, 845–884.Google Scholar
[30] L.Woronowicz, S., Quantum E(2) group and its Pontryagin dual. Lett. Math. Phys. 23(1991), 251–263. http://dx.doi.org/10.1007/BF00398822 Google Scholar
[31] L.Woronowicz, S., Tannaka–Krein duality for compact matrix pseudogroups. Twisted SU(N) groups. Invent. Math. 93(1998), 35–76. http://dx.doi.org/10.1007/BF01393687 Google Scholar