Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T10:01:28.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Order Tangents to Analytic Varieties along Curves. II

Published online by Cambridge University Press:  20 November 2018

Rüdiger W. Braun ,
Reinhold Meise  and
B. A. Taylor
Rüdiger W. Braun
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität, Universitätsstraße 1, 40225 Düsseldorf, Germany e-mail: Ruediger.Braun@uni-duesseldorf.de
Reinhold Meise
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität, Universitätsstraße 1, 40225 Düsseldorf, Germany e-mail: meise@math.uni-duesseldorf.de
B. A. Taylor
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, U.S.A. e-mail: taylor@umich.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 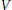$V$ be an analytic variety in some open set in 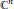${{\mathbb{C}}^{n}}$. For a real analytic curve 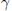$\gamma $ with 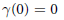$\gamma (0)\,=\,0$ and 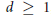$d\,\ge \,1$, define 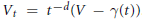${{V}_{t}}\,=\,{{t}^{-d}}(V\,-\,\gamma (t))$. It was shown in a previous paper that the currents of integration over 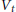${{V}_{t}}$ converge to a limit current whose support 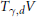${{T}_{\gamma ,d}}V$ is an algebraic variety as 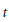$t$ tends to zero. Here, it is shown that the canonical defining function of the limit current is the suitably normalized limit of the canonical defining functions of the 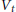${{V}_{t}}$. As a corollary, it is shown that 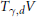${{T}_{\gamma ,d}}V$ is either inhomogeneous or coincides with 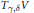${{T}_{\gamma ,\,\delta }}V$ for all 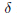$\delta $ in some neighborhood of 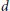$d$. As another application it is shown that for surfaces only a finite number of curves lead to limit varieties that are interesting for the investigation of Phragmén-Lindelöf conditions. Corresponding results for limit varieties 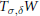${{T}_{\sigma ,\delta }}W$ of algebraic varieties 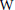$W$ along real analytic curves tending to infinity are derived by a reduction to the local case.

Keywords

32C25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 33 - 63
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bierstone, E. and Milman, P. D., Semianalytic and subanalytic sets. Inst. Hautes Études Sci. Publ. Math. 67(1988), 5–42.Google Scholar
[2] Braun, R.W., Meise, R., and Taylor, B. A., A radial Phragmén-Lindelöf estimate for plurisubharmonic functions on algebraic varieties. Ann. Polon. Math. 72(1999), no. 2, 159–179.Google Scholar
[3] Braun, R.W., Meise, R., and Taylor, B. A., Algebraic varieties on which the classical Phragmén-Lindelöf estimates hold for plurisubharmonic functions. Math. Z. 232(1999), no. 1, 103–135.Google Scholar
[4] Braun, R.W., Meise, R., and Taylor, B. A., Higher order tangents to analytic varieties along curves. Canad. J. Math. 55(2003), no. 1, 64–90.Google Scholar
[5] Braun, R.W., Meise, R., and Taylor, B. A., The geometry of analytic varieties satisfying the local Phragmén-Lindelöf condition and a geometric characterization of partial differential operators that are surjective onA(R4). Trans. Amer. Math. Soc. 356(2004), no. 4, 1315–1383.Google Scholar
[6] Braun, R.W., Meise, R., and Taylor, B. A., Higher order approximations at infinity to algebraic varieties. Note Mat. 25(2005/2006) no. 1, 103–128.Google Scholar
[7] Braun, R.W., Meise, R., and Taylor, B. A., The algebraic surfaces on which the classical Phragmén-Lindelöf theorem holds. Math. Z. 253(2006), no. 2, 387–417.Google Scholar
[8] Chirka, E. M., Complex Analytic Sets. Mathematics and its Applications (Soviet Series) 46, Kluwer, Dordrecht, 1989.Google Scholar
[9] Fulton, W., Algebraic Curves. W. A. Benjamin, New York, 1969.Google Scholar
[10] Hörmander, L., On the existence of real analytic solutions of partial differential equations with constant coefficients. Invent.Math. 21(1973), 151–182.Google Scholar
[11] Fulton, W., The Analysis of Linear Partial Differential Operators. Vol. II, Grundlehren der MathematischenWissenschaften 257, Springer-Verlag, Berlin 1983.Google Scholar
[12] Meise, R., Taylor, B. A., and Vogt, D., Extremal plurisubharmonic functions of linear growth on algebraic varieties. Math. Z. 219(1995), no. 4, 515–537.Google Scholar
[13] Mumford, D.: Algebraic Geometry. I. Complex Projective Varieties. Grundlehren der MathematischenWissenschaften 221, Springer-Verlag, Berlin, 1976.Google Scholar
[14] Whitney, H., Complex analytic varieties. Addison-Wesley, Reading, MA, 1972.Google Scholar