Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T04:57:30.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometric Dilations of Non-Commuting Finite Rank n-Tuples

Published online by Cambridge University Press:  20 November 2018

Kenneth R. Davidson ,
David W. Kribs  and
Miron E. Shpigel
Kenneth R. Davidson
Affiliation:
Department of Pure Mathematics University of Waterloo Waterloo, Ontario N2L 3G1, e-mail: krdavids@uwaterloo.ca
David W. Kribs
Affiliation:
Department of Pure Mathematics University of Waterloo Waterloo, Ontario N2L 3G1, e-mail: dwkribs@uwaterloo.ca
Miron E. Shpigel
Affiliation:
Mitra Imaging Inc. 455 Phillip Street Waterloo, Ontario N2L 1W3, e-mail: mshpigel@mitra.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A contractive $n$-tuple 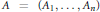$A\,=\,({{A}_{1}},...,{{A}_{n}})$ has a minimal joint isometric dilation 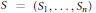$S\,=\,({{S}_{1}},...,{{S}_{n}})$ where the 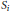${{S}_{i}}$’s are isometries with pairwise orthogonal ranges. This determines a representation of the Cuntz-Toeplitz algebra. When 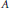$A$ acts on a finite dimensional space, the wot-closed nonself-adjoint algebra $\mathfrak{S}$ generated by $S$ is completely described in terms of the properties of 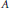$A$. This provides complete unitary invariants for the corresponding representations. In addition, we show that the algebra $\mathfrak{S}$ is always hyper-reflexive. In the last section, we describe similarity invariants. In particular, an $n$-tuple $B$ of 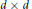$d\,\times \,d$ matrices is similar to an irreducible $n$-tuple 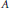$A$ if and only if a certain finite set of polynomials vanish on $B$.

Keywords

47L80
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 3 , 01 June 2001 , pp. 506 - 545
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Arias, A. and Popescu, G., Factorization and reflexivity on Fock spaces. Integral Equations Operator Theory 23 (1995), 268–286.Google Scholar
[2] Arveson, W., Interpolation problems in nest algebras. J. Funct. Anal. 20 (1975), 208–233.Google Scholar
[3] Arveson, W., Subalgebras of C*-algebras III: multivariable operator theory. ActaMath., to appear.Google Scholar
[4] Arveson, W., The curvature invariant of a Hilbert module over C[z1, … , zn]. preprint, 1998.Google Scholar
[5] Azoff, E., Fong, C. K. and Gilfeather, F., A reduction theory for nonself-adjoint operator algebras. Trans. Amer. Math. Soc. 224 (1976), 351–366.Google Scholar
[6] Bercovici, H., Hyper-reflexivity and the factorization of linear functionals. J. Funct. Anal. 158 (1998), 242–252.Google Scholar
[7] Beurling, A., On two problems concerning linear transformations in Hilbert space. Acta Math. 81 (1949), 239–255.Google Scholar
[8] Bratteli, O., Jorgensen, P., and Price, G. L., Endomorphisms of B(H). In: Quantization of nonlinear partial differential equations, (eds.W. Arveson et al), Proc. Symp. Pure Math. 59, Amer.Math. Soc., Providence, 1996, 93–138.Google Scholar
[9] Bratteli, O. and Jorgensen, P., Endomorphisms of B(H) II. J. Funct. Anal. 145 (1997), 323–373.Google Scholar
[10] Bratteli, O. and Jorgensen, P., Iterated function systems and permutation representations of the Cuntz algebra. Mem. Amer. Math. Soc., to appear.Google Scholar
[11] Bunce, J., Models for n-tuples of non-commuting operators. J. Funct. Anal. 57 (1984), 21–30.Google Scholar
[12] Christensen, E., Perturbations of operator algebras II. Indiana Univ.Math. J. 26 (1977), 891–904.Google Scholar
[13] Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
[14] Davidson, K. R., The distance to the analytic Toeplitz operators. Illinois J. Math. 31 (1987), 265–273.Google Scholar
[15] Davidson, K. R. and Pitts, D. R., Invariant subspaces and hyper-reflexivity for free semi-group algebras. Proc. London Math. Soc. 78 (1999), 401–430.Google Scholar
[16] Davidson, K. R. and Pitts, D. R., The algebraic structure of non-commutative analytic Toeplitz algebras. Math. Ann. 311 (1998), 275–303.Google Scholar
[17] Davidson, K. R. and Pitts, D. R., Nevanlinna-Pick Interpolation for non-commutative analytic Toeplitz algebras. Integral Equations Operator Theory 31 (1998), 321–337.Google Scholar
[18] Dyer, J., Pedersen, A. and Porcelli, P., An equivalent formulation of the invariant subspace problem. Bull. Amer. Math. Soc. 78 (1972), 1020–1023.Google Scholar
[19] Frahzo, A., Models for non-commuting operators. J. Funct. Anal. 48 (1982), 1–11.Google Scholar
[20] Frahzo, A., Complements to models for non-commuting operators. J. Funct. Anal. 59 (1984), 445–461.Google Scholar
[21] Friedland, S., Simultaneous similarity of matrices. Adv. in Math. 50 (1983), 189–265.Google Scholar
[22] Glimm, J., Type I C*-algebras. Ann. of Math. 73 (1961), 572–612.Google Scholar
[23] Kribs, D. W., Factoring in non-commutative analytic Toeplitz algebras. J. Operator Theory. to appear.Google Scholar
[24] Kribs, D. W., The curvature invariant of a non-commuting n-tuple. preprint, 2000.Google Scholar
[25] Laca, M., Endomorphisms of B(H) and Cuntz algebras. J. Operator Theory 30 (1993), 381–396.Google Scholar
[26] Popescu, G., Isometric dilations for infinite sequences of noncommuting operators. Trans. Amer.Math. Soc. 316 (1989), 523–536.Google Scholar
[27] Frahzo, A., Multi-analytic operators and some factorization theorems. Indiana Univ.Math. J. 38 (1989), 693–710.Google Scholar
[28] Frahzo, A., Von Neumann Inequality for (B(H)n)1 . Math. Scand. 68 (1991), 292–304.Google Scholar
[29] Frahzo, A., Multi-analytic operators on Fock spaces. Math. Ann. 303 (1995), 31–46.Google Scholar
[30] Frahzo, A., Poisson transforms on some C*-algebras generated by isometries. J. Funct. Anal., to appear.Google Scholar
[31] Powers, R., An index theory for semigroups of *-endomorphisms of B(H) and type II factors. Canad. J. Math. 40 (1988), 86–114.Google Scholar
[32] Radjavi, H. and Rosenthal, P., Invariant subspaces. Ergebnisse der Math. und ihrer Grenz. 77, New York, Heidelberg, Berlin, Springer-Verlag, 1973.Google Scholar
[33] Sarason, D., On spectral sets having connected complement. Acta Sci. Math. (Szeged) 26 (1965), 289–299.Google Scholar
[34] Nagy, B. Sz., and Foiaş, C., Harmonic analysis of operators on Hilbert space. North Holland Pub. Co., London, 1970.Google Scholar
[35] Wermer, J., On invariant subspaces of normal operators. Proc. Amer.Math. Soc. 3 (1952), 270–277.Google Scholar